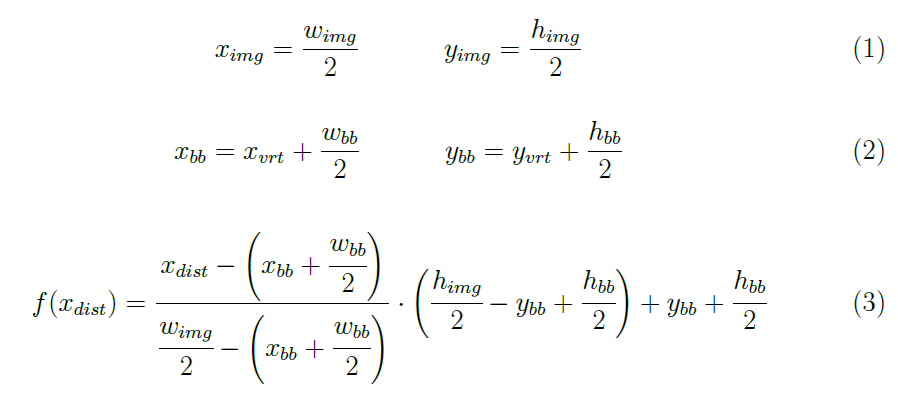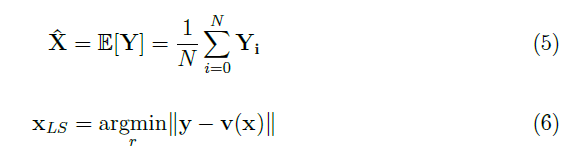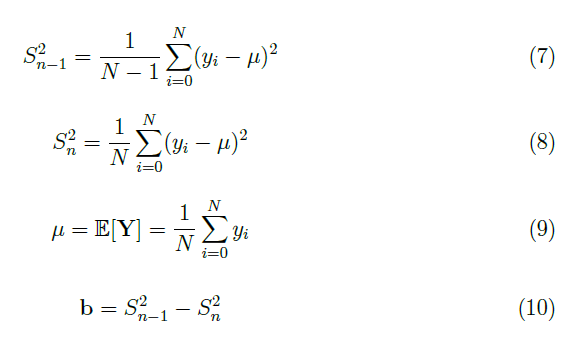Corso sugli Aeromobili a Pilotaggio Remoto partendo da zero: controllo automatico del volo

Continua il corso dedicato agli Aeromobili a Pilotaggio Remoto (APR). Nell'articolo precedente abbiamo descritto il modello matematico di un multi-rotore, in particolare quello di un esacottero, utilizzando due differenti approcci: Eulero-Lagrange e Newton-Eulero. Ricavate le equazioni del moto ne è stata espressa l'equivalente rappresentazione nella forma dello spazio di stato. Nell'appuntamento di oggi analizzeremo una delle tecniche di possibile impiego per sintetizzare, dall'insieme delle rilevazioni che contornano il target, un'unica bounding box che lo delimiti. Successivamente, verrà descritto il processo utilizzato per l'estrazione delle informazioni in merito alla posizione assoluta del drone all'interno dello scenario virtuale (continuo dell'esempio preso in considerazione nei precedenti episodi). Tali informazioni sono necessarie, al controllo del volo, per variare la posa dell'aeromobile di modo da non perdere di vista il target. Infine, è introdotta la dinamica del velivolo, il conseguente controllo in traiettoria e le simulazioni ottenute che comprovano il funzionamento dell'intero sistema, contestualizzando, nella vita reale, l'utilizzo di tale tecnologia.

Calcolo della bounding box

Illustrati i passi che hanno consentito di ottenere un modello in grado di riconoscere l'auto all'interno dell'ambiente virtuale - illustrato nel secondo articolo di questo mini corso - in questo paragrafo analizzeremo lo script impiegato per ricavare, dall'insieme delle rilevazioni che contornano il veicolo, un'unica bounding box. La stessa box impiegata per l'estrazione delle informazioni (paragrafo successivo) necessarie al sistema di volo per l'attuazione della legge di controllo.

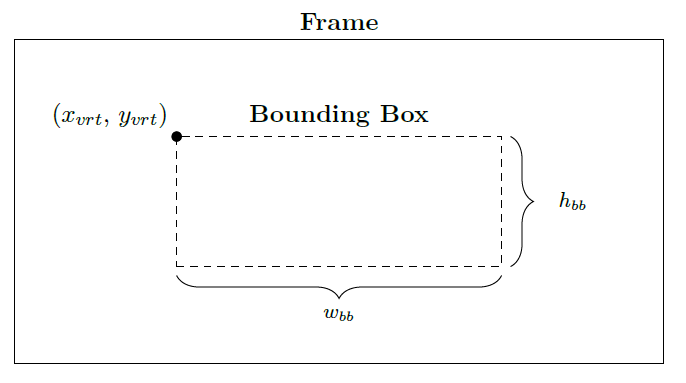
Lo script, fissato il numero di immagini campione, riconosce il target all'interno dei singoli frame ottenendo così, per ogni fotogramma, l'insieme delle bounding box che contornano l'auto. Da ogni finestra (Figura 1) ne estrae la posizione del frame, espressa in coordinate (x_vrt, y_vrt), altezza (h_bb) e larghezza (w_bb), per poi calcolarne la massima, in termini di area occupata, e quella media.

Figura 1: Struttura bounding box ottenuta dal processo di detection.

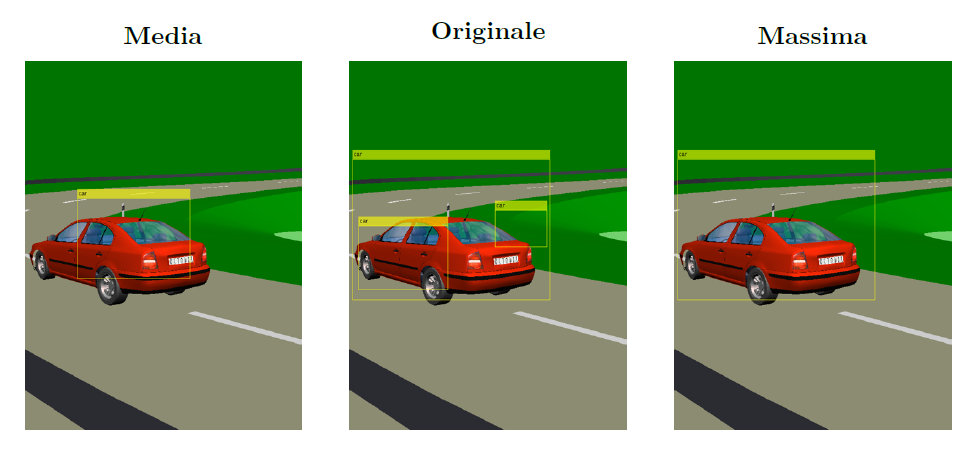
La finestra media da poca fiducia all'algoritmo di riconoscimento sintetizzato, considerando la presenza di eventuali falsi positivi (concetto espresso nel precedente appuntamento), generando così un controsenso: realizzato l'algoritmo di riconoscimento, non si ha fiducia delle rilevazioni ottenute e pertanto si introduce un onore computazionale maggiore per il calcolo della bounding box media. Tale è la ragione per cui si è deciso di impiegare la prima delle due soluzioni proposte (la massima finestra) per la sintesi di un'unica bounding box che delimiti l'autovettura. Tale scelta non è vincolante per il funzionamento del sistema, in maniera del tutto equivalente si può pensare di utilizzare la bounding box media oppure quella ottenuta attraverso una tecnica diversa che, ad esempio, attribuisce un peso alla distanza tra i due centroidi: quello dell'auto e quello della bounding box. I tests comparativi condotti hanno validato la scelta fatta, evidenziando prestazioni migliori a fronte di una riduzione dell'onere computazionale.

Figura 2: Esempio di bounding box media e massima.

In Figura 2 è riportato il risultato della detection condotta su di un'immagine campione, la relativa bounding box media, ottenuta mediando aritmeticamente le finestre presenti nell'insieme delle rilevazioni, e quella massima. Come si può vedere, la finestra massima inquadra maggiormente il target, migliorando così il sistema di controllo che regola l'avvicinamento/allontanamento dell'APR dal veicolo.

Estrazione delle informazioni

Ottenuta un'unica bounding box che contorna il target è necessario estrarre informazioni in merito alla sua posizione all'interno del frame. Tali dati sono fondamentali per il sistema di controllo che varia la posa del drone, all'interno dello scenario, di modo da non perdere di vista l'autovettura (uscita dal suo campo visivo).

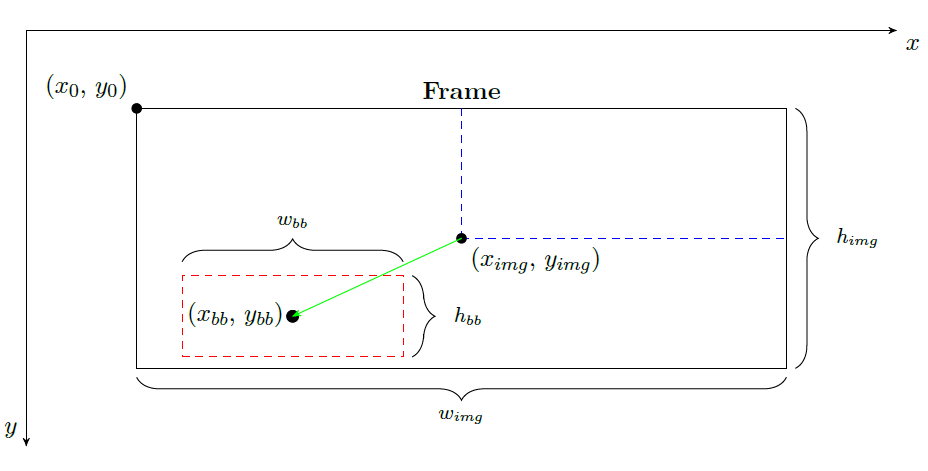
Si è proceduto, quindi, a realizzare uno script che calcola per ogni fotogramma, esportato dall'ambiente virtuale, il centroide dell'immagine (x_img, y_img), quello della bounding box (x_bb, y_bb), ed il vettore distanza tra i due centroidi f(x_dist):

dove, nel caso in esame, w_img=600 px, h_img=800 px (rispettivamente larghezza ed altezza del frame), h_bb e w_bb (altezza e larghezza della bounding box) variano ad ogni rivelazione, mentre x_dist è il vettore costituito dall'insieme dei punti, sull'asse delle ascisse, che separano i due centroidi.

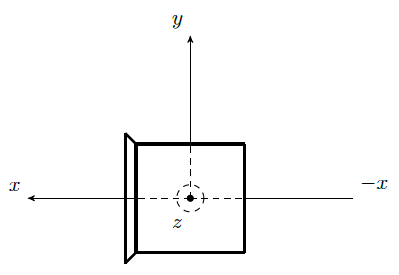
In Figura 3 è rappresentato schematicamente quanto sopra discusso. I due centroidi, riferiti rispetto allo spigolo superiore sinistro (x₀, y₀), sono indicati con due pallini pieni, mentre il vettore distanza f(x_dist) è rappresentato in verde. L'obiettivo del sistema di controllo è minimizzare tale vettore, agendo sull'orientamento dell'aeromobile: imabardata (ψ), beccheggio (θ) e rollio (φ).

Figura 3: Schema del processo di estrazione delle informazioni.

Il processo di estrazione consente, però , di ottenere solo una stima della posizione relativa, e non assoluta [La posizione assoluta non è funzione della posizione dell'osservatore, al contrario di quella relativa], dell'autovettura all'interno dello scenario. La posizione, infatti, è riferita sempre rispetto al centro dell'immagine (x_img, y_img) che non costituisce un sistema di riferimento inerziale ma in realtà è un sistema assi-corpo. Al fine di ricavare la posizione assoluta è fondamentale tenere in conto anche i parametri della fotocamera, considerando dunque il modello pinhole camera ideale (tipico degli ambienti di realtà virtuale, caratterizzato dall'assenza di lenti quindi distorsione), quali FOV (Field Of View), lunghezza focale (f), angolo di visione (α), e così via. Tali caratteristiche non sono state prese in considerazione per scelta progettuale: le ipotesi semplificative hanno consentito di ridurre al minimo i tempi di sviluppo, rimandando l'approfondimento a lavori successivi.

Reference Generator

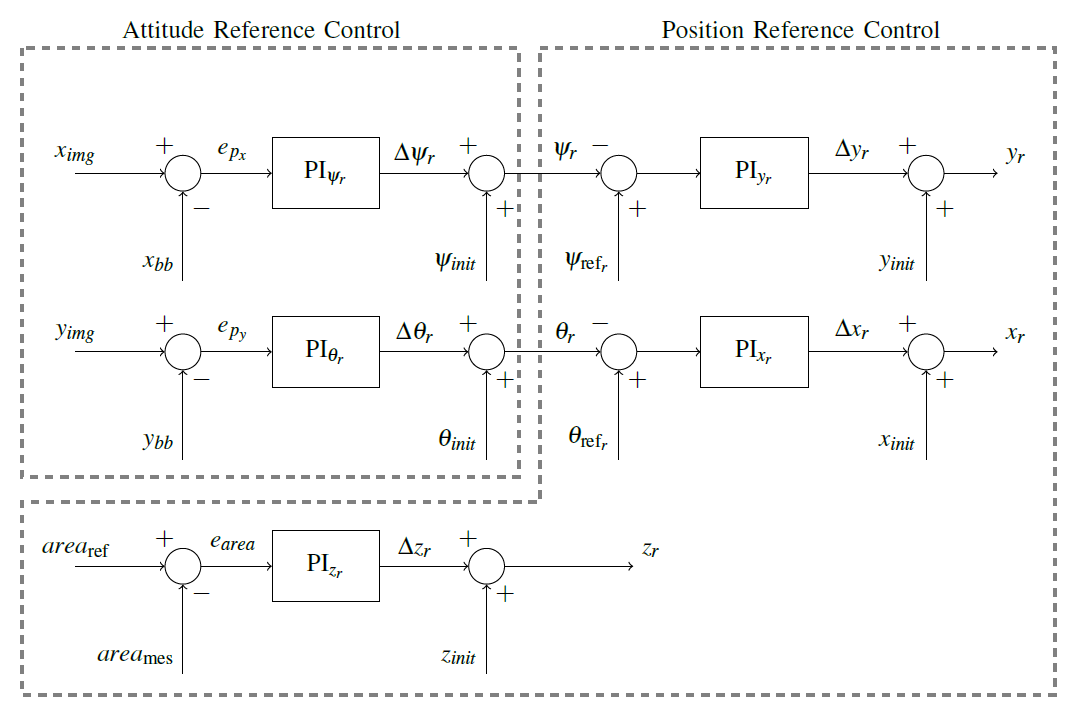
Capito come estrarre le informazioni dai singoli fotogrammi, si è passati alla progettazione del generatore di riferimenti (Figura 4). Lo schema di controllo utilizza le proiezioni del vettore distanza f(x_dist), lungo l'asse delle ascisse (e_px) e quello delle ordinate (e_py), per variare i riferimenti di orientamento dell'aeromobile.

Figura 4: Rappresentazione schematica del reference generator.

L'obiettivo del controllo di orientamento è minimizzare il vettore distanza (il cui modulo, direzione e verso variano ad ogni frame), agendo sui tre angoli di imbardata (ψ_r), beccheggio (θ_r) e rollio (φ_r), di modo che il centroide dell'immagine (x_img, y_img) coincida con quello della bounding box (x_bb, y_bb), valori di riferimento per il controllo della dinamica. Al primo frame, l'angolo di rollio è mantenuto volutamente a zero al fine di evitare rotazioni del velivolo che possano portare miss detection, conseguentemente l'uscita del target dal campo visivo dell'APR. Al contrario, nei fotogrammi successivi esso assume il valore imposto dalla dinamica dell'aeromobile. Tale ipotesi non è limitativa, se si suppone che l'autovettura abbia una dinamica più lenta di quella del drone, perché meramente funzione delle sue caratteristiche.

L'obiettivo, quindi, del reference generator (controllo ad alto livello) è generare una traiettoria di riferimento sulla base delle immagini acquisite dallo scenario virtuale. Tale traiettoria è poi inseguita da un secondo sistema di controllo (controllo a basso livello) che determina i comandi (U₁, U₂, U₃, U₄, vedi puntata precedente) da inviare al velivolo affinché lo stesso si porti lungo il percorso desiderato, entro un certo errore.

Il generatore di riferimenti è disaccoppiato: due PI in parallelo agiscono su due dei sei DOFs del drone (ψ_r e θ_r). I guadagni K_p=1·10⁵ e K_i=1·10³ sono stati scelti in modo tale da tenere in conto del verso di crescenza degli angoli nello scenario virtuale (Figura 5). Le uscite, però, non sono direttamente gli angoli di ψ_r e θ_r da inviare al controllo di posizione (del generatore di riferimenti) bensì la loro variazione (Δψ_r e Δθ_r), a cui vanno sommati gli angoli (ψ_init e θ_init) che identificano l'orientamento iniziale del velivolo.

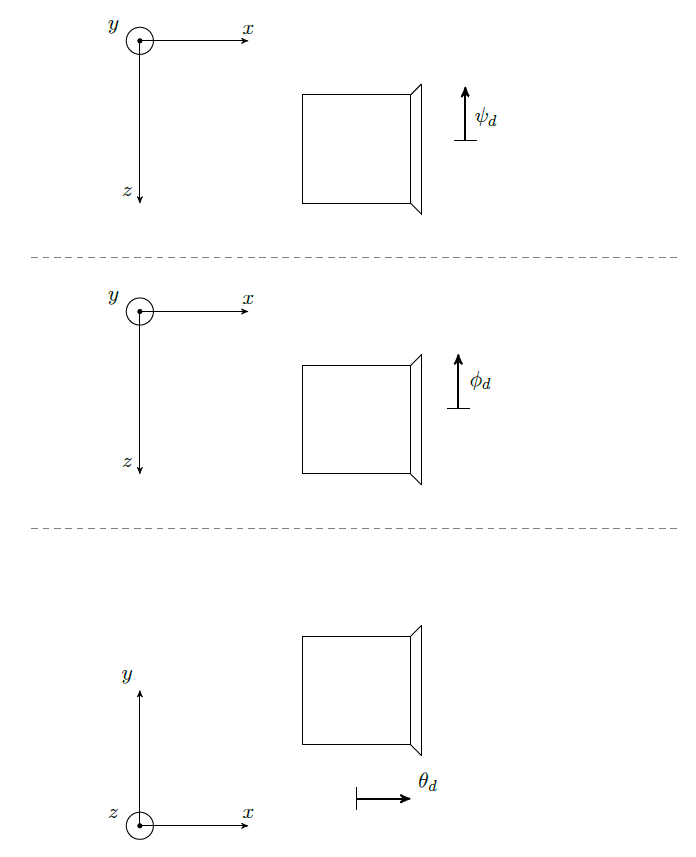
Figura 5: Verso di crescenza degli angoli di beccheggio, rollio ed imbardata nello scenario virtuale.

Viceversa, il controllo di posizione non è disaccoppiato perché funzione delle uscite del precedente (ψ_r e θ_r), come si evince dallo schema in Figura 4. Tali uscite sono confrontate rispettivamente con ψ_rif e θ_rif, ovvero l'orientamento di riferimento che si desidera assuma il velivolo durante il tracking del target. Entrambi sono fissati di modo da mantenere l'APR sempre in asse con il piano orizzontale, portando conseguentemente ad un innalzamento/abbassamento della quota (movimenti trasversali) o ad uno spostamento in avanti/indietro (movimenti longitudinali). Tali valori prendono in considerazione la posizione iniziale della camera nello scenario virtuale, riportata in Figura 6.

Figura 6: Posizione iniziale camera nel VR di Matlab.

Identicamente a quanto visto con il controllo di orientamento, due PI in parallelo agiscono su due dei sei DOFs dell'aeromobile (y_r e x_r) , i cui guadagni sono rispettivamente K_p,yr=1, K_i,yr=2, K_p,xr=1.5 e K_i,xr=40. Ancora una volta, le uscite del sistema di controllo non rappresentano direttamente le posizione (y_r e x_r) del velivolo all'interno dello scenario, ma ne indicano le variazioni (Δy_r e Δx_r) a cui vanno sommate le posizioni iniziali (y_init e x_init) che identificano lo stato del drone al primo frame.

Per quanto concerne il controllo sull'ultimo DOFs (z_r) il discorso è leggermente diverso. Mentre nel caso precedente il segnale di errore era dato dalla differenza tra l'angolo misurato e quello di riferimento, sia esso di imbardata oppure beccheggio, in questo caso è pari allo scarto tra l'area di riferimento (area_rif) e l'area misurata (area_mis).

Con il termine area misurata si intende l'area della finestra che contorna l'autovettura, banalmente data dal prodotto area_mis=w_bb·h_bb. Al contrario, l'area di riferimento è calcolata sull'insieme delle immagini utilizzate per il processo di training del classificatore - secondo articolo del mini-corso -, acquisite sorvolando l'autovettura percorrendo una traiettoria ad aspirale alla distanza di 15 m (analizzata con la dovuta attenzione nel paragrafo successivo). In sintesi, il confronto tra le aree viene utilizzato per capire quanto ci si discosta dalla distanza di riferimento (15 m) che si desidera il drone mantenga dal veicolo durante l'inseguimento del target.

In maniera del tutto equivalente ai casi precedenti, il sistema di controllo è realizzato con un PI i cui guadagni sono pari a K_p,zr=1·10^-6 e K_i,zr=1·10^-5. Altra costante rispetto al caso precedente, il controllo non è direttamente la posizione z_r che l'aeromobile deve assumere nello scenario, ma la sua variazione (Δz_r) a cui va sommata la posizione iniziale (z_init) assunta al primo istante di simulazione.

Concludendo, il controllo del volo analizzato è progettato impiegando tecniche euristiche e discretizzato utilizzando Backward Eulero, avente come obiettivo la minimizzazione dell'errore (e_px, e_py, e_area, etc).

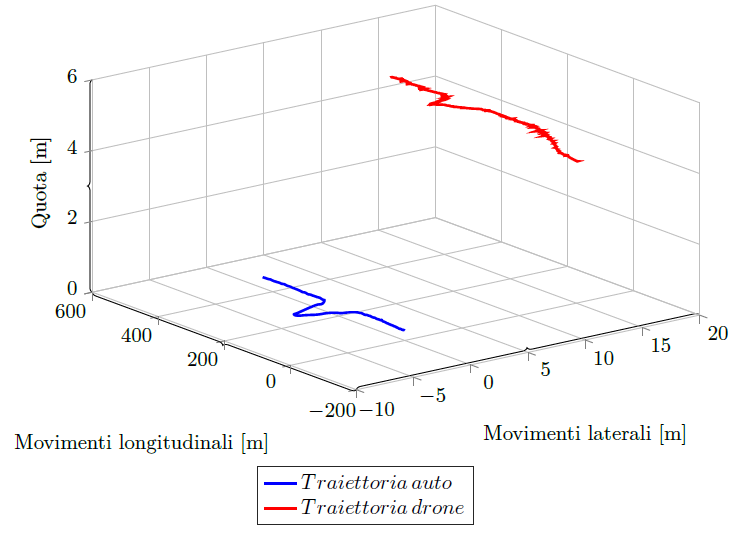
In Figura 7 è riportato il grafico che presenta la traiettoria assunta dal veicolo e dall'APR durante l'intera simulazione priva della dinamica e, conseguentemente, del controllo in traiettoria. L'obiettivo è testare il funzionamento del sistema ad alto livello prima di inglobare il successivo. L'autovettura si muove di un tratto rettilineo, per poi affrontare una piccola curva, ed infine percorre l'ultimo tratto nuovamente in linea retta. Al link è presente il video che mostra il funzionamento del sistema nel suo complesso.

Figura 7: Traiettoria APR ed auto nel VR di Matlab.

Dal grafico in Figura 7 si può notare che l'aeromobile si trova già in volo prima di intraprendere l'inseguimento dell'auto. Questa è una mera casualità, e non influisce minimamente sulle prestazioni dell'algoritmo. Il velivolo è, infatti, capace di muoversi in completa autonomia estraendo semplicemente le informazioni presenti all'interno delle immagini.

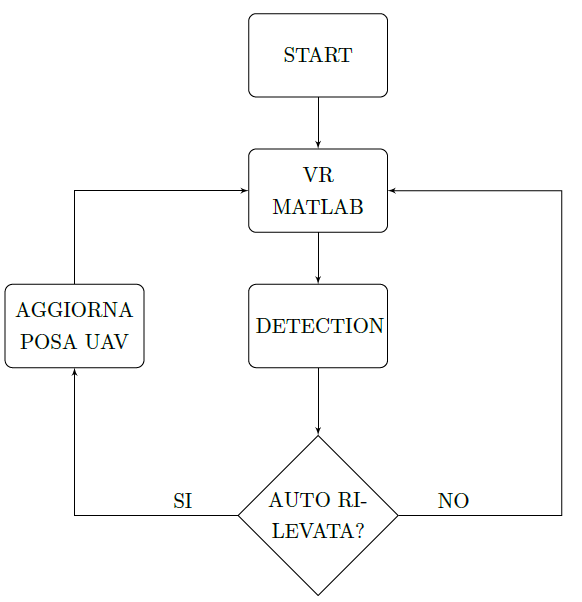
Quanto sopra discusso viene attuato se e solo se l'autovettura è identificata all'interno del frame, in caso contrario il drone rimane sospeso in area (hovering) fino al termine della simulazione o al riconoscimento dell'autovettura, come riportato nel diagramma di flusso in Figura 8.

Figura 8: Diagramma di flusso reference generator.

Stima area di riferimento

Prima di leggere questa sezione si suggerisce, per chi non avesse mai sentito parlare di distribuzione statistiche, di leggere quanto presente in un relativo articolo.

Per la stima dell'area non è possibile utilizzare lo stimatore MVU (Minimum Variance Unbiased) o quello ML (Maximum Likelihood) perché non vi una conoscenza statistica degli osservabili (le misure di area). Inoltre, un così basso numero di osservazioni non giustifica il passaggio per la ECDF (Empirical Cumulative Distribution Function). In questo caso un'alternativa è lo stimatore naturale (eq. 5) o la stima LS (Least Square, eq. 6):

dove ||y-v(x)|| è l'errore di misura.

Entrambi non richiedono la conoscenza statistica della caratterizzazione degli osservabili, la scelta tra l'uno o l'altro è funzione solo del valore assunto dalla varianza.

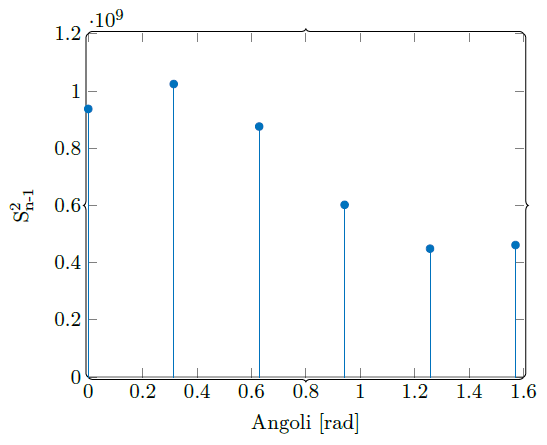
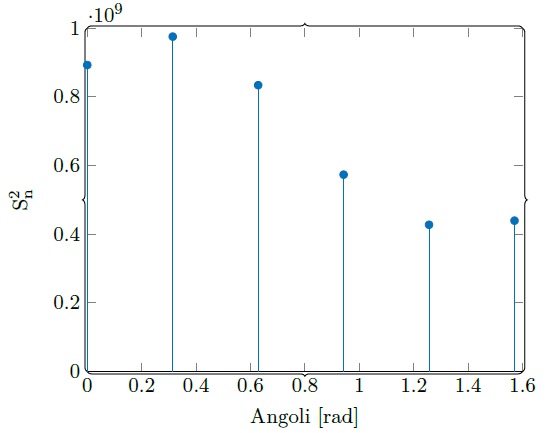
Al fine di stimare la varianza ed il bias (eq. 10), indici di qualità di uno stimatore, è stata impiegata la varianza campionaria non polarizzata (corretta, eq. 7) e quella polarizzata (eq. 8), mostrate rispettivamente in Figura 9 e 10.

dove N è il numero di immagini utilizzate nel processo di training del classificatore.

Figura 9: Varianza campionaria corretta.

Figura 10: Varianza campionaria polarizzata.

Il bias (Figura 11) è due ordini di grandezza più piccolo della varianza (il grafico di confronto tra le varianze è riportato in Figura 12), per questo è stato trascurato (S_n-1²≈S_n²). Stesso ragionamento per la varianza comparata alle aree delle bounding box: una piccola varianza indica che i data point tendono a chiudersi al valore vero. Tale è la ragione per cui è stata utilizzata la media campionaria, chiamata anche stimatore naturale, per la stima dell'area della finestra che contorna l'auto. Il valore di riferimento così ottenuto è di 32 376 px².
[...]

ATTENZIONE: quello che hai appena letto è solo un estratto, l'Articolo Tecnico completo è composto da ben 3584 parole ed è riservato agli ABBONATI. Con l'Abbonamento avrai anche accesso a tutti gli altri Articoli Tecnici che potrai leggere in formato PDF per un anno. ABBONATI ORA, è semplice e sicuro.