Dentro un computer quantistico: il teletrasporto quantistico

Si, lo so, la prima cosa che avete pensato leggendo il titolo di questo articolo è “Star Trek”. È comprensibile. Al di là di come e quanto la scatola dei sogni forgi il nostro immaginario, è innegabile che il teletrasporto sia qualcosa che un pò tutti leghiamo alla fantascienza, sia essa cinematografica o cartacea. Pochi sanno però che il teletrasporto (una sua forma, perlomeno) è da un bel pezzo che ha tinto d’inchiostro la carta dei libri di fisica, ed è da qualche anno che si è fatto strada nei laboratori. Si, per chi lo scoprisse solo adesso, il teletrasporto (una sua forma, perlomeno) è stato realizzato nel “mondo reale”. È una delle applicazioni dell’entanglement quantistico che sta eliminando il “fanta” dalla scienza e già per questo si merita qualche parola. Accendete quindi i motori a curvatura, e partiamo!

NO, STAR TREK E' UN’ALTRA COSA

Questo titolo per dire che, se parlando di teletrasporto quantistico vi aspettate il gatto di Schrodinger che ricompare allegro e miagolante su un altro pianeta, dovrò darvi una cocente delusione. Mentre il teletrasporto in Star Trek è fisico, nel senso che si trasporta fisicamente della materia da un capo all’altro dell’universo, quello quantistico riguarda solo informazione. (Si potrebbe opinare che un oggetto fisico contiene un bel pò di informazione e che, in fin dei conti, per ricostruirlo dall’altra parte sia sufficiente trasferire solo il suo contenuto informativo; non è del tutto errato, ma questa è ancora fantascienza!) Tuttavia, se siete sopravvissuti alla scorsa volta, quando vi ho parlato dell’entanglement, ricorderete forse che la trasmissione di informazione attraverso di esso è impossibile in quanto, oltre a offendere la memoria di Albert Einstein, è condizionata all’esito della misura su uno stato quantistico. Essendo questi esiti del tutto casuali, e quindi non prevedibili a priori, si può si trasmettere a distanza, ma non si può decidere cosa trasmettere e questo, di fatto, equivale a non mandare informazione. Ma si può fare, in qualche altro modo? Ovviamente si, e il motivo più semplice è una variante del principio antropico: se non si potesse, non saremmo qui a parlarne!

La vera domanda quindi è: come si può fare? Lasciate che a spiegarvelo siano i due eroi del campo della teoria dell’informazione (e della crittografia, e delle telecomunicazioni, e delle reti di trasmissione e di un sacco di altre cose), Alice e Bob. Alice e Bob si trovano dunque per le mani questi due bit entangled. A questi due bit, sempre in memoria di Albert Einstein e dei suoi due compari Podolski e Rosen, si dà spesso il nome di “coppia EPR”. Diciamo che sanno che questi bit si trovano nello stato di Bell:

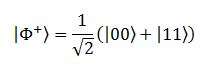
e sanno anche che, se Alice misurasse nella base canonica:

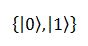
“forzerebbe” il bit di Bob ad assumere lo stesso valore: se Alice ottenesse, dopo la misura, uno zero, anche Bob, se andasse a misurare il suo qubit, otterrebbe uno zero; se Alice ottenesse un uno, anche Bob otterrebbe un uno. L’azione è istantanea e a distanza, Einstein si rivolta nella tomba ma, come Alice e Bob sanno molto bene, così facendo non riescono a trasmettersi informazione, perché Alice non può pilotare il risultato della sua misura. Tra l’altro, uno schema di questo tipo è anche meno che pratico; in una situazione più “reale” ciò che Alice vorrebbe trasmettere a Bob non è uno zero o un uno, ma un qualche qubit:

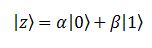
che lei possiede. Si tratta di un qubit ignoto, sospeso in una qualche sovrapposizione di zero e uno (non necessariamente in parti uguali, visto che non abbiamo specificato i coefficienti), che Alice vuole trasmettere senza sapere quali siano i coefficienti, perché in effetti l’unico modo che ha per determinarli è eseguire delle misure e, come non ci stancheremo mai di ripetere, una misura altera lo stato del qubit, distruggendo di fatto ciò che era prima della misura stessa. Questo generico qubit però non è entangled con nulla, quindi, si chiede Alice, non è che posso usare in qualche modo la coppia entangled che condivido con Bob per trasmettere z? In pratica, potrei mai riuscire a trasmettere il mio qubit attraverso il canale quantistico creato dalla coppia EPR?

RIPARTIRE DALLA BASE

Alice e Bob, in quanto esperti del settore, sanno bene che spesso la soluzione del problema la si trova rovistando nei sacri testi. In Star Trek ciò che sembra accadere è che prima l’oggetto viene smaterializzato da una parte, e poi ricostruito dall’altra. Bob ha già l’altra metà della coppia EPR, perfetta e intonsa. E se Alice distruggesse la sua metà, e nel fare questo costringesse la metà di Bob a diventare il bit che vuole trasmettere? “Distruggere”, in questo campo, significa “misurare”, perché (forse l’abbiamo già detto?) la misura altera i qubit (ad esempio facendoli passare da uno stato sovrapposto ad un valore ben preciso); inoltre, se la misura la si esegue su una parte di una coppia EPR, l’operazione si manifesta dall’altro lato. L’idea di Alice sarebbe dunque quella di eseguire una misura sulla sua metà della coppia così che l’altra metà diventi ciò che vuole trasmettere. Teoricamente sembra avere senso. Funzionerà? Vediamo. Il punto cruciale qui è la misura. Alice e Bob (e magari anche noi) sanno già che misurare nella base canonica non consente di trasmettere informazione, perché il risultato è casuale. Ma Alice e Bob (e forse noi no) sanno anche che non devono necessariamente misurare nella base canonica; possono misurare in una base qualsiasi.

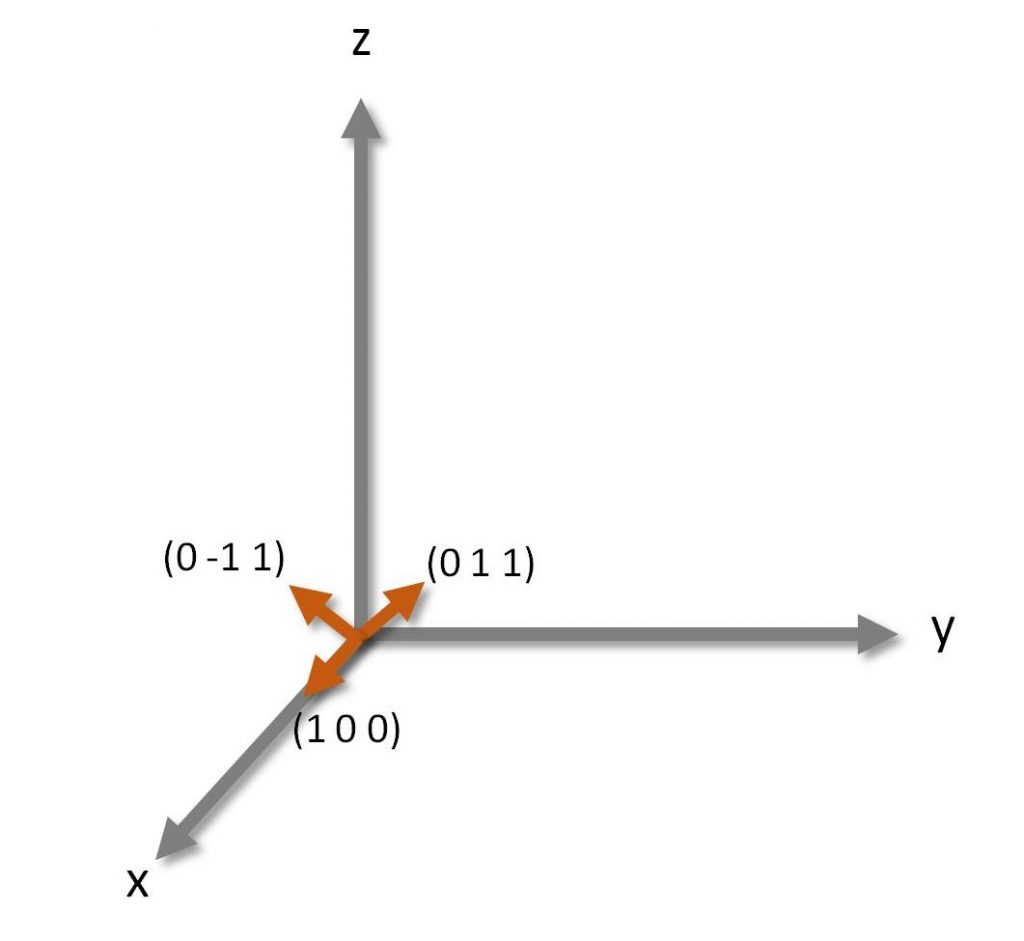
Figura 1: Base alternativa nello spazio 3D

La cosa non è tanto sorprendente né arcana se si ricorda perché la nostra base preferita nello spazio 3D sia quella con i tre versori x, y e z perpendicolari tra loro, con il piano xy a fare da “terreno” e con z perpendicolare ad esso: perché è comoda. Perché è così che ci appare il mondo. Prendete il caso della Figura 1. La base con i tre vettori ruotati di 45° è perfettamente legittima, ma è anche orribilmente scomoda da usare e quindi ha poco senso anche solo pensare di sceglierla. Questo è un discorso che in fisica vale molto più in generale. Il sistema di riferimento in cui si analizza un problema non deve sempre e comunque essere quello canonico, può essere qualsiasi, e di solito viene scelto in modo tale che il problema sia facile da risolvere. Si può ad esempio prendere il riferimento cartesiano “classico” e centrarlo su un oggetto in movimento, così che l’oggetto sia fermo rispetto ad esso, oppure si può passare alle coordinate polari se l’oggetto che si sta studiando ha qualche genere di simmetria sferica o cilindrica (in pratica, se assomiglia ad una sfera o ad un cilindro).

Il concetto di misura, il “che cosa significa” misurare, in una base diversa da quella canonica resta lo stesso, e questo Alice lo sa benissimo. Se Alice misura nella base canonica, può sapere quanto spin up o spin down ci sono nel suo qubit; se Alice misura nella base:

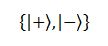
può sapere quanto spin destra e spin sinistra ci sono nel suo qubit. Ma se questo vale per qualsiasi scelta di base, perché non misurare in una base più consona per il problema in questione? Stiamo trafficando con bit entangled, quindi perché non lavorare con la base di Bell?

Di nuovo, vediamo.

Chi deve effettuare queste misure è Alice, perché è lei che ha il qubit da trasmettere. Il sistema quantistico, dal suo punto di vista, è fatto da tre particelle: il qubit z e i due qubit della coppia EPR. Lo stato di questo sistema è il solito prodotto:

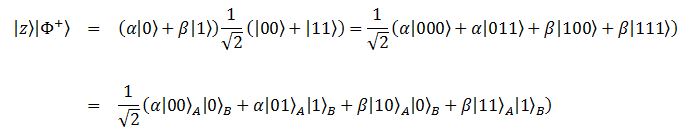
La scelta dei pedici discende dal fatto che Alice ha in mano due bit e Bob uno soltanto. Alice adesso deve misurare nella base di Bell. Tuttavia, lo stato scritto in questo modo non ci è particolarmente d’aiuto. Se ricordate, per misurare nella base canonica lo stato è bene averlo scritto nella forma:

dove i vari c sono i coefficienti che ci dicono quanto è probabile che troviamo, dopo la misura, le due particelle nello stato corrispondente. Volendo misurare nella base di Bell, dovremmo riscrivere lo stato così:

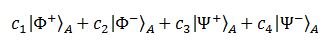
Ma riscrivere lo stato in questa forma non è difficile, basta usare le identità:

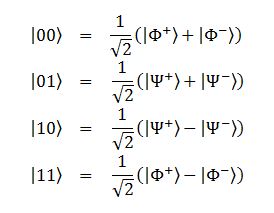
che potete verificare in un attimo semplicemente buttando dentro le definizioni degli stati di Bell. Queste identità ci permettono di riscrivere lo stato che Alice si ritrova per le mani come:

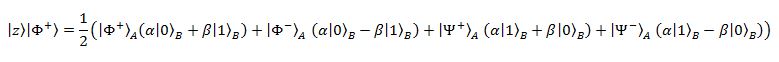
Questo stato ci dice un pò di cose interessanti. È fatto da quattro parti, ciascuna delle quali con coefficiente 1\2, il che significa che la misura ha quattro risultati possibili, e tutti e quattro hanno la stessa probabilità (25%) di saltare fuori. Questi quattro risultati influenzano, come accade sempre quando c’è l’entanglement di mezzo, la parte della coppia EPR in mano a Bob. Prendiamo il primo risultato possibile:

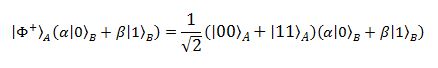
Significa che un quarto delle volte che esegue la misura, Alice si ritroverà per le mani il bit z correlato alla sua metà della coppia EPR! La misura nello stato di Bell, a tutti gli effetti, altera la correlazione tra le particelle, spostandola dai due bit della coppia al bit z e una delle sue metà! Se Alice andasse a misurare il suo bit z, infatti, non lo troverebbe più nello stato ignoto di sovrapposizione in cui era all’inizio, ma correlato con l’altro bit in suo possesso. La cosa ancora più stupefacente è che adesso la particella di Bob si trova nello stato: [...]

ATTENZIONE: quello che hai appena letto è solo un estratto, l'Articolo Tecnico completo è composto da ben 2872 parole ed è riservato agli ABBONATI. Con l'Abbonamento avrai anche accesso a tutti gli altri Articoli Tecnici che potrai leggere in formato PDF per un anno. ABBONATI ORA, è semplice e sicuro.