Le due più grandi rivoluzioni della fisica del novecento, meccanica quantistica e relatività generale, si occupano di concetti diametralmente opposti: l’infinitamente piccolo e l’infinitamente grande. Cose più distanti tra loro sono difficili da immaginare. Tuttavia, se c’è una cosa che hanno in comune, è il terrore che incutono in chi vi si avvicina. Questo terrore deriva da due aspetti principali: la complessità concettuale, e quella matematica. Ma, se sulla prima non si può obiettare, come nemmeno sulla seconda nel caso della relatività, qualcosa da ridire la potrei avere sulla difficoltà dei calcoli in meccanica quantistica, soprattutto nel contesto che mi interessa qui, ossia quello degli algoritmi per computer quantistici. Come ho sentito dire una volta, nel momento in cui accetti i formalismi, per lavorare con un computer quantistico, tutto ciò che ti occorre sapere è un pò di algebra lineare.
(QUASI) TUTTO È UN VETTORE
Fortuna (o sfortuna) vuole che l’algebra lineare sia uno dei campi della matematica più astratti in circolazione. Fortuna, perché il bello delle cose astratte è che un teorema applicato ad una cosa eterea quale è uno spazio vettoriale lo puoi riutilizzare su qualunque cosa riesci a modellizzare con uno spazio vettoriale, il che capita davvero per un sacco di cose. Sfortuna, perché spesso è difficile capire di che si sta parlando. Che cos’è uno spazio vettoriale? Un insieme di vettori. Ottimo. La classica risposta che dice tutto e nulla. Cos’è un vettore? Non rispondete “la freccetta nello spazio cartesiano”, per favore. Non è abbastanza generale. Per quanto le freccette cui ci abitua la fisica siano sicuramente dei vettori, non è assolutamente vero che tutti i vettori siano freccette.
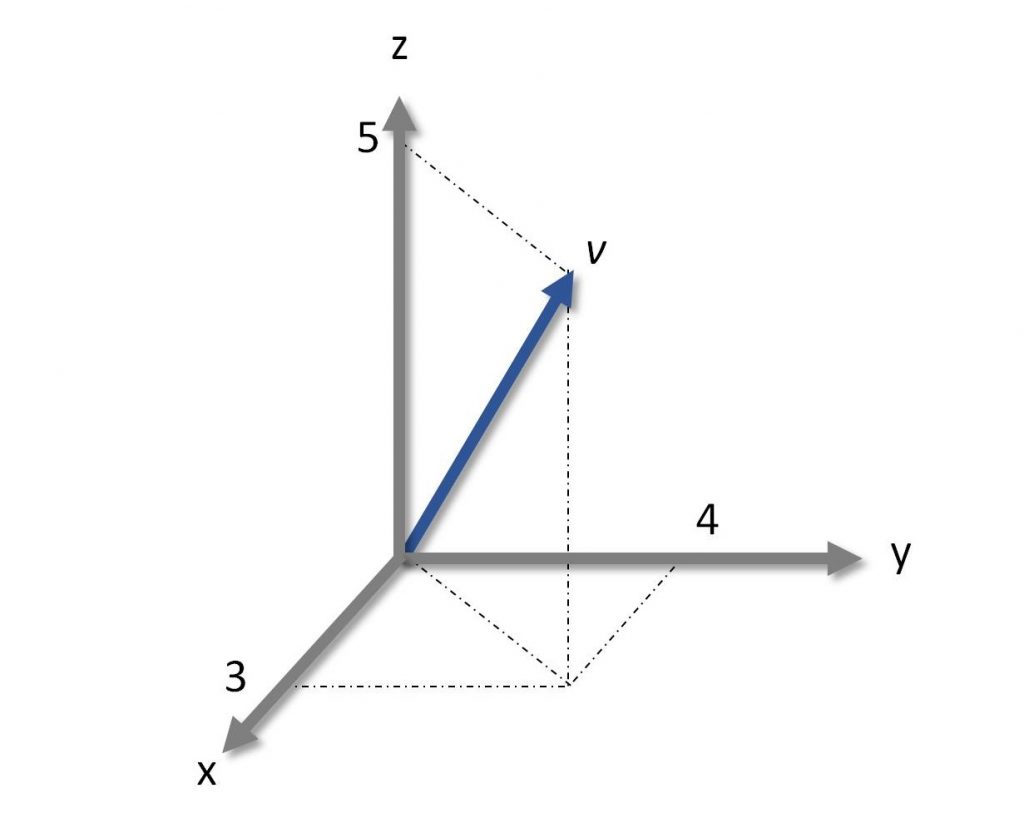
Figura 1: Un vettore banale
Un esempio? Qualsiasi sequenza di numeri del tipo
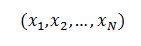
è un vettore. Quindi, la freccetta nello spazio cartesiano, fondamentalmente, è una di queste cose qua: tre numeri a cui attribuiamo il significato di coordinata x, y, e z. Ma c’è molto di più. I polinomi possono essere visti come vettori, come pure le matrici stesse. E, cosa ancora più assurda, una funzione può essere vista come un vettore.
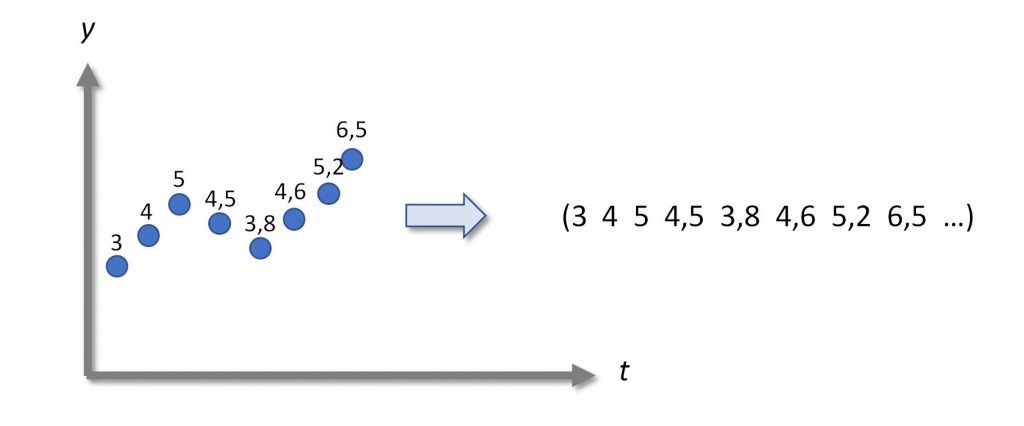
Figura 2: Una funzione trasformata in vettore
Quest’affermazione va presa con un pò di cautela. Sì, un vettore è una sequenza di numeri, quindi in linea di principio potremmo prendere tutti i punti di una funzione, metterli tra parentesi separate da virgole e farci un vettore. Molto banalmente, come nella Figura 2. La differenza sostanziale è che una funzione è una sequenza infinita di punti. Questo ci crea sicuramente dei problemi, dal momento che avere a che fare con quantità infinite non è mai indolore, per cui bisogna chiedersi: vale la pena farlo? La risposta giusta è sempre quella dell’ingegnere saggio: dipende. Dipende se riusciamo a guadagnarci qualcosa. Prendiamo per esempio (così, a caso), l’equazione di Schrodinger indipendente dal tempo, nella sua forma più generale:
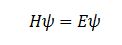
È chiaro che nei sistemi fisici reali la dipendenza dal tempo non può mancare, ma complica di brutto i calcoli e comunque questa qui è più che sufficiente in molti casi. Qui, ψ è la funzione d’onda, ed è appunto una funzione che descrive lo stato della nostra particella/gruppo di particelle. Ci dice, in pratica, che sta facendo la particella, dove si trova, come si muove, che ha mangiato a cena, ecc. H è detta Hamiltoniana, ed è un operatore: è un qualcosa che, applicato alla funzione d’onda, la modifica. L’Hamiltoniana rappresenta il modo in cui il sistema agisce sulla particella/gruppo di particelle. Se, ad esempio, ciò che stiamo studiando fosse un elettrone in un reticolo cristallino, ψ ci direbbe lo stato della particella, e H in che modo il reticolo (e quindi tutti gli atomi in esso) condizionano e influenzano l’elettrone. Dall’altro lato dell’uguale abbiamo di nuovo la funzione d’onda moltiplicata però per un numero, che in questo caso ha il significato di energia della particella. In pratica, l’equazione di Schrodinger ci dice che, se prendiamo un elettrone descritto da una certa funzione d’onda e lo mettiamo in un qualche sistema fisico, il sistema fisico in questione altererà la funzione d’onda semplicemente scalandola per una qualche costante ben precisa.
Ora, se, come abbiamo detto, una funzione è vettore di lunghezza infinita, allora questa equazione, riesumando vecchi e polverosi ricordi di algebra lineare, è semplicemente una equazione agli autovalori. Per quanto possa sembrare qualcosa di strano ed esotico, un’equazione agli autovalori è semplicemente un’equazione in cui una matrice applicata ad un vettore restituisce il vettore moltiplicato per una costante. Risolvere un’equazione del genere significa, data la matrice, ricavare il vettore (chiamato, in questo contesto e senza troppa fantasia, autovettore) e il coefficiente (ancora meno fantasiosamente chiamato autovalore). E, la cosa bella, è che le tecniche di soluzione di queste equazioni sono ben note (si fanno al primo anno di università): dunque, nel momento in cui riusciamo a mettere H sotto forma di matrice, partendo dall’assunto che anche ψ è un vettore, sappiamo perfettamente come risolvere l’equazione di Schrodinger! E, cosa ancora più importante, per i poteri a noi conferiti dall’algebra lineare, sappiamo che tutti i risultati relativi ad autovalori ed autovettori valgono anche per le funzioni d’onda. Primo tra tutti, quelli relativi al concetto di base.
TRE VETTORI PER UNIRLI TUTTI
Quando usiamo tre coordinate per descrivere un punto nello spazio, senza neanche rendercene conto stiamo riuscendo a fare una cosa all’apparenza incredibile: descrivere uno spazio infinito con semplicemente una terna di numeri! Per noi è una cosa perfettamente naturale; del resto, che altro modo c’è per descrivere un oggetto nello spazio se non tramite altezza, larghezza e profondità? Alle prese con una faccenda del genere, un matematico inizierebbe a farsi tutta una serie di domande che non sfiorerebbero mai la mente di un comune mortale. Come posso formalizzare questo concetto? Vale solo in questo caso o lo si può generalizzare? È l’unico modo possibile? E via dicendo. E dalla risposta a queste domande il matematico tira fuori uno dei concetti più importanti e profondi dell’algebra lineare. Altezza, larghezza e profondità li possiamo usare per descrivere tutto il nostro spazio tridimensionale, senza bisogno di aggiungere altri parametri, per due motivi fondamentali:
- Sono sufficienti per descrivere tutti i punti dello spazio
- Sono necessari tutti e tre, nel senso che non possiamo descrivere l’altezza di un oggetto usando semplicemente larghezza e profondità
Considerando che lo spazio 3D in cui viviamo è oggettivamente uno spazio vettoriale (ci fanno disegnare freccette fin da quando eravamo alle elementari!), il matematico si sbilancia fino ad arrivare a dire che questi vettori “fondamentali”, l’insieme minimo di vettori che ci permette di costruire tutto lo spazio deve esistere per qualsiasi spazio vettoriale, sia esso fatto di numeri, polinomi, funzioni o boccali di birra. A questo insieme si da il nome di base, e di tutti gli altri vettori che si possono costruire a partire dalla base si dice che sono una loro combinazione lineare.
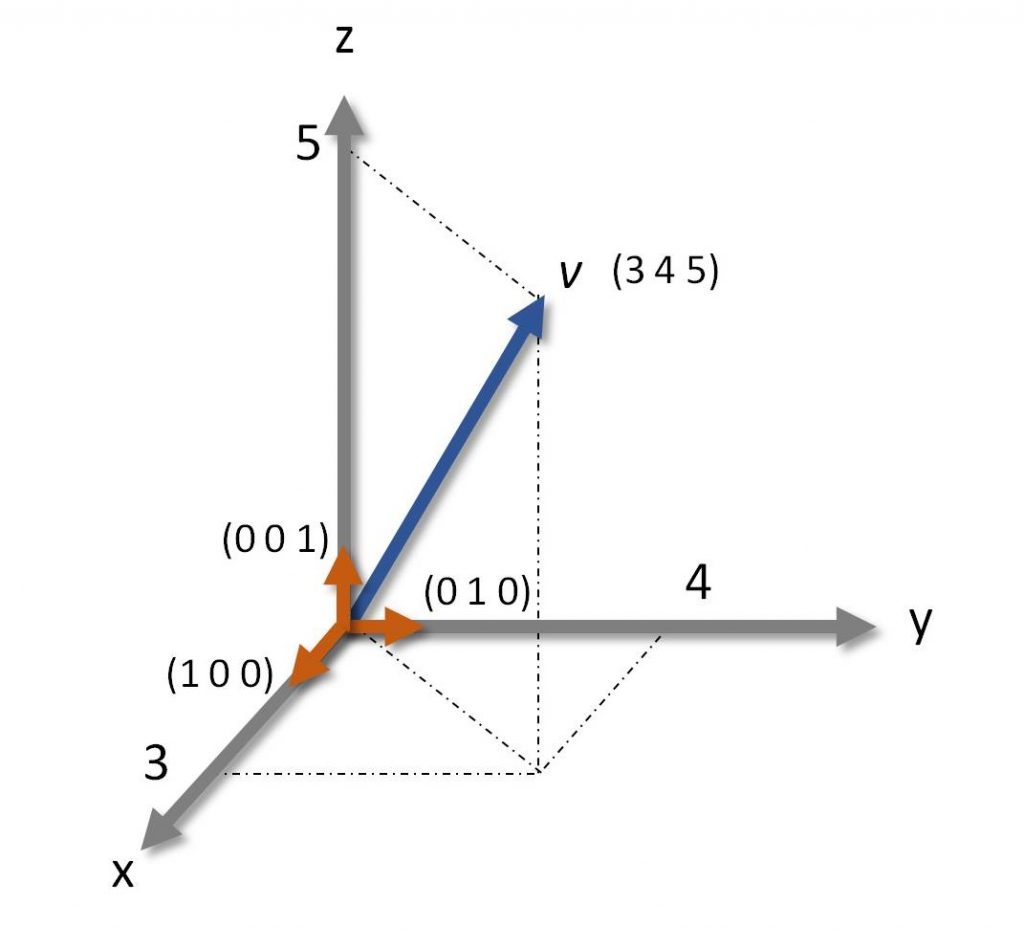
Figura 3: Base nello spazio 3D
Prendiamo al solito come esempio lo spazio 3D. La base è formata dai tre vettori diretti lungo i tre assi cartesiani, come nella Figura 3, giusto? Ora, un vettore lungo l’asse x avrà solo la lunghezza, un vettore lungo l’asse y avrà solo la profondità mentre uno lungo z avrà solo l’altezza. Dunque, i tre vettori della base li possiamo scrivere come:
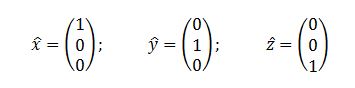
Prendiamo adesso un punto a caso nello spazio:
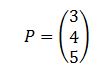
È abbastanza evidente come questo vettore possa essere scritto come somma pesata dei tre vettori della base:
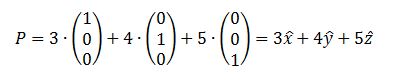
E questo vale sempre, indipendentemente da che cosa ci sia dentro lo spazio vettoriale o quanto possano essere complicati i vettori che compongono la base. Un esempio. Se il nostro spazio è di funzioni, inevitabilmente anche i vettori che compongono la base dovranno essere funzioni, e dovranno essere funzioni tramite le quali possiamo costruire tutte le altre. Per fare questo, ci servono però dei coefficienti con cui scalare i nostri “vettori” prima di sommarli tra loro per ricostruire la funzione desiderata. È esattamente come facciamo nello spazio 3D con altezza, larghezza e profondità.
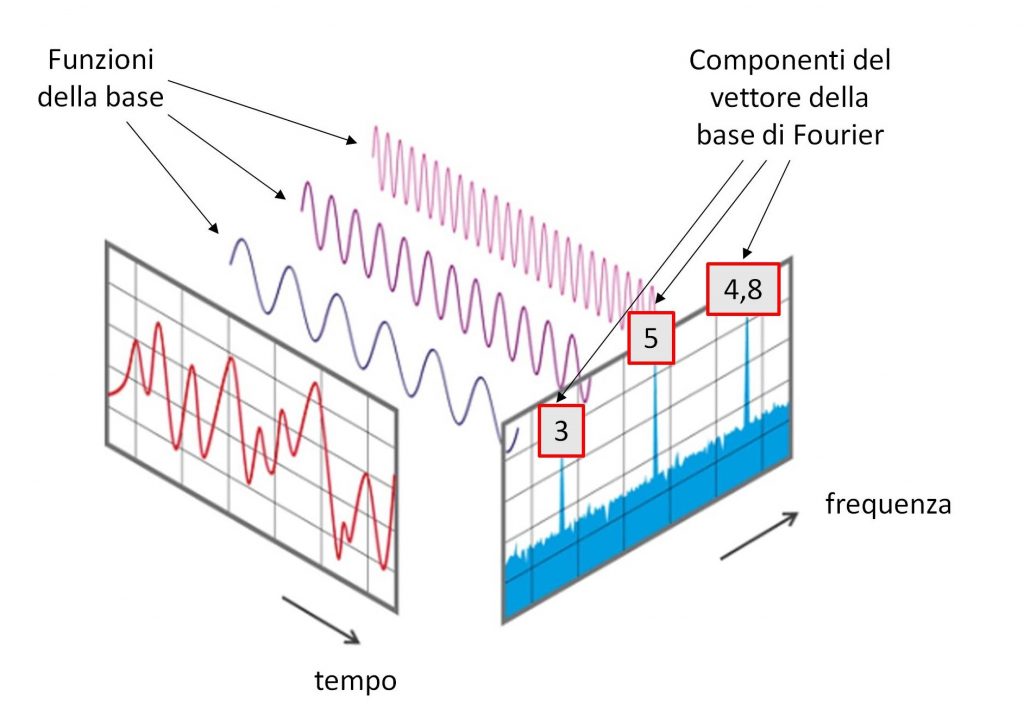
Figura 4: La trasformata di Fourier
Se la campanella non ha ancora squillato, vi do un aiutino: questo è esattamente ciò che fa la trasformata di Fourier. La trasformata di Fourier prende una funzione e ne tira fuori un certo numero di coefficienti; a partire da questi coefficienti, la funzione di partenza può essere ricostruita sommando un altrettanto certo numero di seni e coseni, come accade nella Figura 4. In questo contesto, i coefficienti estratti dalla trasformata di Fourier sono i numeri che andranno a riempire il vettore, mentre i seni e coseni sono le funzioni della base. Dato un certo spazio vettoriale, come tirar fuori una base e le regole per calcolare i coefficienti sono un altro paio di maniche che non è il caso di rimboccarsi in questo momento. La cosa importante è che c’è un altro risultato dell’algebra lineare (e che in quanto tale vale per qualsiasi spazio vettoriale, e che ci permette di tornare all’equazione di Schrodinger) che dice che ogni spazio vettoriale ammette una base di autovettori. Questo risultato è fenomenale. Ci dice che, nel momento in cui troviamo le soluzioni dell’equazione di Schrodinger, ricaviamo la base di quel particolare spazio, quello descritto dalla H che lo caratterizza. E, nel momento in cui abbiamo la base, possiamo ricostruire tutte le funzioni d’onda che possono esistere in questo contesto: in altre parole, possiamo descrivere il comportamento di tutte le particelle nel momento in cui le si mette nel sistema descritto da questa particolare H. “Descrivere” una particella, in questo contesto, equivale a ricavare la sua combinazione lineare in termini dei vettori della base, così come per descrivere un appendiabiti occorre ricavare la sua altezza, larghezza e profondità. Dobbiamo ricavare i coefficienti. Nel caso della trasformata di Fourier ci sono le formule; nel caso più generale, c’è il concetto di misura.
ATTENZIONE: quello che hai appena letto è solo un estratto, l'Articolo Tecnico completo è composto da ben 3237 parole ed è riservato agli ABBONATI. Con l'Abbonamento avrai anche accesso a tutti gli altri Articoli Tecnici che potrai leggere in formato PDF per un anno. ABBONATI ORA, è semplice e sicuro.