
I progettisti di circuiti analogici impiegano in notevole misura programmi di simulazione per prevedere le prestazioni dei circuiti. Il valore di un simulatore dipende dalla precisione con cui può prevedere risultati reali e dalla velocità con cui li può produrre. Una discrepanza tra prestazioni simulate e reali può far sì che un prodotto debba passare attraverso costosi cicli di debug iterativi.
Per la simulazione di circuiti analogici si impiega SPICE poiché questo programma può calcolare l’andamento completo di segnali con ampie variazioni in circuiti arbitrari. Tre metodi numerici utilizzati in SPICE ne spiegano il successo nella simulazione di circuiti analogici. Specificamente:
- il metodo dell’iterazione di Newton per determinare la soluzione di circuiti in cui sono presenti elementi non lineari;
- i metodi della matrice sparsa per racchiudere matrici enormi nello spazio di indirizzamento di un computer realizzabile praticamente;
- il metodo dell’integrazione implicita per integrare le equazioni differenziali risultanti dalle reattanze presenti nel circuito.
La capacità di un simulatore SPICE di produrre affidabilmente risultati esatti dipende dall’accuratezza con cui si implementano questi metodi. Il presente articolo illustra perché LTspice è superiore ad altre implementazioni di SPICE nel produrre risultati esatti.
Iterazione di Newton
Comporta lo sviluppo della curva I-V di ciascun dispositivo non lineare del circuito in una serie di Taylor, troncata ai primi due termini, e quindi nel risolvere il sistema di equazioni lineari simultanee che ne deriva. Se la soluzione del sistema di equazioni lineari è esattamente il punto centro dello sviluppo della serie di Taylor, poiché l’approssimazione è esatta in tale punto e accurata nel suo intorno, la soluzione del sistema di equazioni è proprio la corretta soluzione del circuito non lineare originalei. Il successo della convergenza dei risultati dell’iterazione di Newton comporta l’individuazione di una prova numerica che la corretta soluzione del circuito è stata trovata.
La robustezza dell’iterazione di Newton dipende da due fattori: (1) nessuna delle curve I-V degli elementi del circuito deve avere discontinuità di valori o di pendenza; (2) tutti gli elementi non lineari devono essere bypassati con una capacità affinché la soluzione all’incremento temporale precedente sia un buon punto di inizio per l’iterazione di Newton a partire dall’incremento temporale attuale. Le condizioni (1) e (2) sono soddisfatte da qualsiasi circuito fisico, ma i programmi SPICE in genere non le implementano correttamente poiché i dispositivi a semiconduttore utilizzati in Berkeley SPICE hanno discontinuità e questi errori di implementazione si ripercuotono sui risultati. Queste discontinuità non si verificano in LTspice.
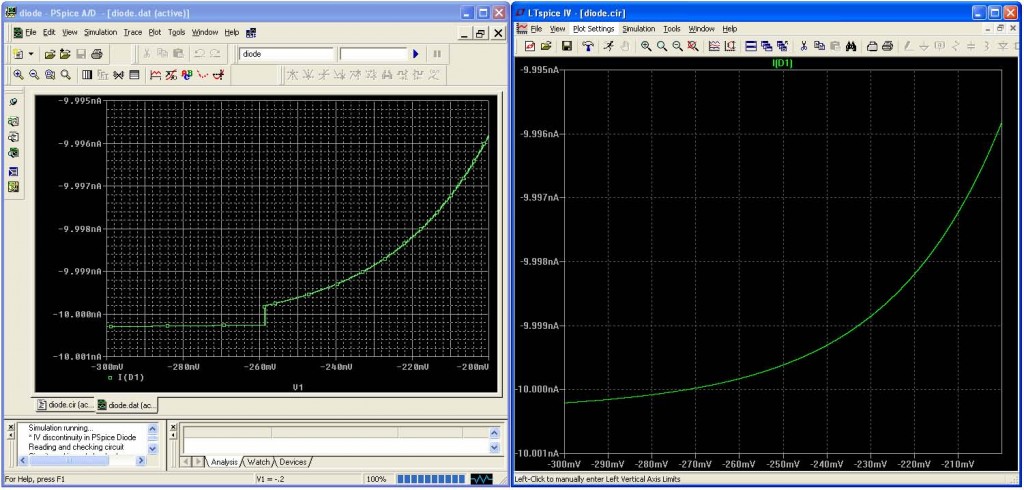
Per esempio, la Figura 1 mostra la curva I-V di un diodo in PSpiceii rispetto a LTspice. La netlist utilizzata in ciascun caso è
* Discontinuità I-V nel diodo PSpice
V1 N001 0 0
D1 N001 0 D
.dc V1 -.3 -.2 2u
.probe
.model D D(Is=10n)
.end
La curva I-V del diodo in PSpice è discontinua per quanto riguarda sia il valore che la pendenza. Tali discontinuità esistono nella maggior parte dei dispositivi a semiconduttore in PSpice ma in nessuno dei dispositivi a semiconduttore in LTspice.
Metodi della matrice sparsa
La serie di Taylor è multidimensionale: una dimensione per ciascun nodo di tensione ignota del circuito. Per un circuito integrato analogico, si possono avere 100.000 nodi di tensione distinti e quindi una matrice di conduttività di 100.000 per 100.000 ossia 80 miliardi di byte per coefficienti della matrice a doppia precisione. Anche gli attuali processori a 64 bit non offrono linee di indirizzamento in numero sufficiente per accedere a una tale quantità di memoria. Fortunatamente, quasi tutti i coefficienti sono nulli e quindi non devono essere memorizzati. I metodi della matrice sparsa tengono traccia solo degli elementi diversi da zero; ciò permette di risolvere una matrice enorme in uno spazio di indirizzamento comparativamente ridotto.
La sparsità della matrice deriva dalla natura fisica dei circuiti pratici: la maggior parte dei nodi è collegata solo ad alcuni altri nodi. Ad esempio, anche se si scrive la matrice di conduttività di un circuito che sembra una rete di resistori con un numero enorme di maglie, la matrice è quasi diagonale poiché ciascun nodo è collegato resistivamente solo a nodi adiacenti. I circuiti pratici non hanno una densità di connessioni pari, ad esempio, a quella dei nodi di una rete da pesca. La sparsità di un circuito analogico complesso si misura in parti per milione ed è tale sparsità che consente di risolvere la matrice con un computer di oggi. L’iterazione di Newton per i circuiti analogici non sarebbe possibile senza metodi della matrice sparsa.
La similarità tra le varie implementazioni di SPICE risiede in questi metodi della matrice sparsa. Tutti i programmi SPICE utilizzano la decomposizione LU. La maggior parte delle implementazioni di SPICE utilizza una libreria di matrici sparse derivate dal programma distribuito con il programma SPICE dell’Università di Berkeley, ma alcune, in genere commercializzate come “SPICE veloci”, cercano di migliorarlo utilizzando una libreria di matrici sparse perfezionata, come SuperLUiii.
Un approccio migliore consiste semplicemente nel fare eseguire i calcoli al processore al limite FLOP teorico dell’hardware impiegato. Il problema è che occorre più tempo per trasferire i dati numerici alla FPU di quello effettivamente necessario per eseguire la FLOP.
La pipeline della FPU in genere funziona vuota; in definitiva, questa è una conseguenza del fatto che tutti i sistemi operativi utilizzano l’allocazione dinamica della memoria. Quando il simulatore viene scritto e compilato, la posizione di memoria in cui risiedono i dati della matrice è ignota. Al runtime, il simulatore richiede la memoria con la chiamata di funzione malloc(), che restituisce un indirizzo al quale il simulatore può memorizzare in sicurezza i dati della matrice. Poiché non è umanamente possibile assegnare a ciascun elemento della matrice un nome diverso, si utilizzano array. Ciò significa che il simulatore chiede parti di memoria in numero inferiore ma più grandi, e i coefficienti individuali vengono indicizzati secondo l’indirizzo della base restituito da malloc(). Nella fase di compilazione del simulatore, è noto solo l’indirizzo della base che consente l’indicizzazione necessaria per raggiungere l’elemento della matrice. Risolvere questo indirizzo al runtime e acquisire i dati a cui tale indirizzo punta nella FPU richiede più tempo dell’esecuzione della FLOP stessaiv. Nel caso ideale, gli indirizzi dei dati necessari per un calcolo sarebbero noti prima della fase di calcolo, così che i dati potrebbero essere acquisiti con efficienza e la FPU non dovrebbe attenderli.
LTspice elimina le operazioni aggiuntive necessarie per l’acquisizione dei dati da parte della FPU mediante codice in linguaggio assembly automodificante scritto in fase di runtime, dopo che la memoria della matrice è stata allocata e gli indirizzi restituiti da malloc() sono noti. Questo codice creato nella fase finale può risolvere indirizzi concreti degli elementi della matrice in linea con il codice affinché i dati possano essere caricati con efficienza, consentendo alla FPU di funzionare con la pipeline piena dopo che il codice è stato assemblato e collegato mediante l’assembler e il linker incorporati di LTspice. LTspice è unico nell’implementare un metodo di soluzione di matrice sparsa automodificante, autoassemblante e autocollegante. Questo metodo ottiene risultati notevolmente migliori rispetto a qualsiasi altra tecnica.
Integrazione implicita
La simulazione di un circuito analogico richiede l’integrazione numerica di equazioni differenziali per determinare l’andamento dei segnali ai capi dei condensatori e degli induttori. Qui è dove si osservano le differenze principali tra le varie implementazioni di SPICE: nei metodi disponibili per l’integrazione di equazioni differenziali.
L’integrazione numerica comporta errori, e la simulazione di un circuito analogico comporta l’integrazione di andamenti di segnale in presenza di molti costanti di tempo. La caratteristica intrinseca dell’integrazione di equazioni differenziali che hanno soluzioni del tipo exp(-costante*tempo) è che gli errori si sommano fino a un valore infinito a meno di non usare un metodo numerico denominato integrazione implicitav. Senza quest’ultima, in SPICE non sarebbe possibile l’analisi dei transitori.
SPICE utilizza un’integrazione del secondo ordine; la maggior parte delle implementazioni di SPICE segue Berkeley SPICE e offre due metodi di integrazione implicita del secondo ordine: di Gear e trapezoidalevi. Il metodo di integrazione trapezoidale è più veloce e preciso del metodo di Gear, ma può generare artefatti numerici tali che la soluzione integrata su incrementi temporali discreti oscilla da un incremento all’altro rispetto al vero andamento continuo nel tempo; ciò può far nascere dubbi sulla correttezza del simulatore anche se ciascun trapezoide contiene la corretta area integrata.
Le oscillazioni causate dal metodo di integrazione trapezoidale sono state ritenute inaccettabili da progettisti di circuiti analogicivii in misura tale che questo metodo è stato eliminato da Pspice – un’implementazione commerciale di SPICE – lasciando l’integrazione con il metodo di Gear, più lento e meno preciso, come la sola scelta disponibile.
Ma l’integrazione con il metodo di Gear non smorza le sole oscillazioni numeriche ma tutte le oscillazioni, anche quelle fisiche, facendo sì che un circuito malfunzionante nella realtà, a causa di un’oscillazione, nella simulazione appaia perfettamente stabile e funzionale poiché l’instabilità è stata eliminata mentre venivano smorzate le oscillazioni numeriche. Ciò ha condotto a situazioni disastrose, in cui un circuito integrato da progettare viene simulato in PSpice, se ne completa il layout e lo si fabbrica per scoprire alla fine che non funziona a causa di un’instabilità non rilevata dall’integrazione con il metodo di Gear impiegato da PSpice. È così necessario un ciclo di revisione della maschera – a un costo considerevole e con notevole spreco di tempo – per rimuovere l’instabilità nel tentativo di ottenere la funzionalità iniziale.
In linea di principio, l’errore di integrazione generato con il metodo di Gear potrebbe essere ridotto se il progettista del circuito integrato specificasse un basso valore per il massimo incremento temporale; ma questa non è una soluzione fattibile perché (1) incrementi temporali ridotti rallentano enormemente la velocità della simulazione, e (2) comunque non c’è modo di assicurare che l’incremento temporale sia sufficientemente piccolo.
La documentazione di Pspice afferma che viene utilizzato un metodo di Gear modificato e in verità sembra che il simulatore sia più efficace nel selezionare un incremento temporale sufficientemente piccolo da ridurre l’errore rispetto all’implementazione del metodo di Gear in Berkeley SPICE.
Ma il metodo adottato da Pspice spesso non ottiene risultati validi. È facile creare un circuito semplicissimo e osservare come il risultato determinato mediante integrazione numerica da PSpice devii drasticamente dalla vera soluzione determinabile tramite esame diretto del circuito.
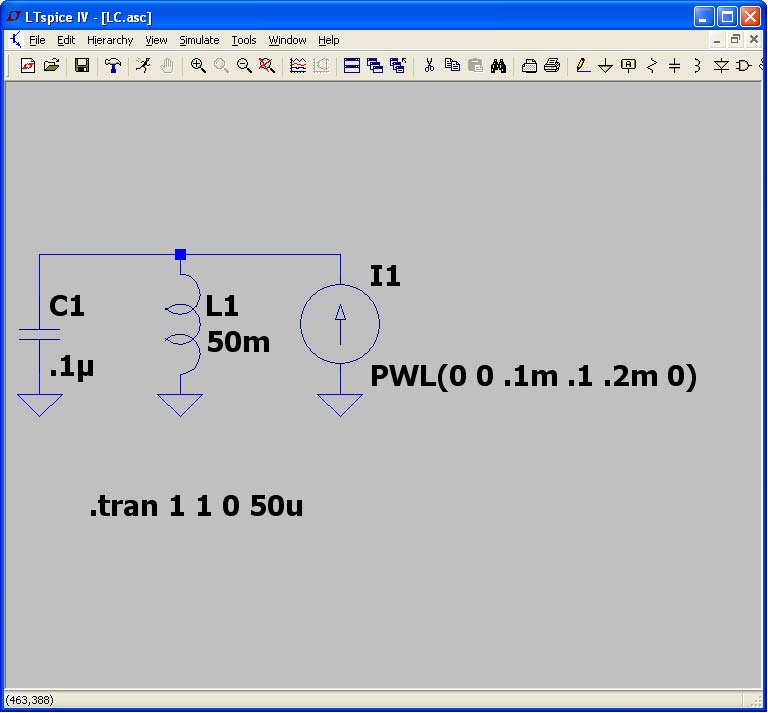
Si consideri la Figura 2, che mostra un circuito risonante LC parallelo alimentato da un generatore di corrente lineare a tratti, che produce un picco di corrente durante i primi 0,2 ms e poi rimane a zero.
La soluzione dovrebbe essere che l’applicazione del picco di corrente eccita il circuito risonante LC parallelo, che continua a oscillare ad ampiezza costante dopo che la corrente è cessata. La netlist del circuito è data da
* Errore di integrazione Gear (PSpice)
L1 N001 0 50m
I1 0 N001 PWL(0 0 .1m .1 .2m 0)
C1 N001 0 .1u
.tran 1 1 0 50u
.probe
.end
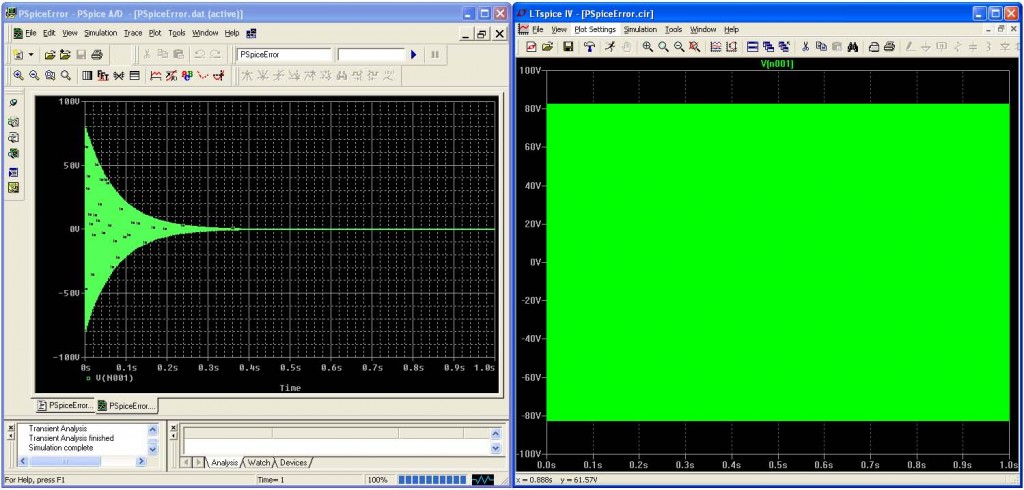
La Figura 3 mostra che l’integrazione con il metodo di Gear modificato impiegata in Pspice smorza artificialmente le oscillazioni, mentre LTspice fornisce immediatamente la corretta soluzione. L’errore in PSpice può essere ridotto specificando un valore inferiore per il massimo incremento temporale (il quarto valore nell’istruzione .tran). Questo dovrebbe essere un circuito semplice da analizzare con il metodo di Gear modificato adoperato in PSpice. Ma per Pspice è fondamentalmente impossibile risolvere con affidabilità un circuito con molte costanti di tempo tutte differenti a meno che l’ingegnere non verifichi manualmente come la “soluzione” converge mentre si specificano valori sempre più piccoli del massimo incremento temporale.
La Figura 3 mostra chiaramente che il metodo di Gear impiegato in Pspice non integra correttamente le due reattanze di un circuito semplicissimo, che presenta un solo nodo. La caratteristica intrinseca dell’errore dell’integrazione con il metodo di Gear è di fare apparire i circuiti più stabili nella simulazione di quanto non lo siano effettivamente nella realtà.
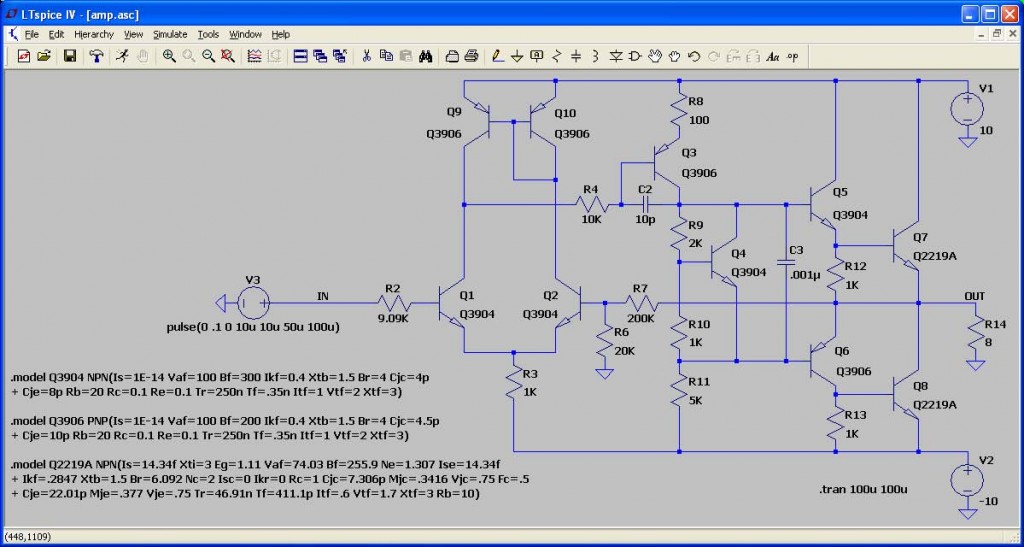
Per illustrare le conseguenze di questo errore tramite un esempio pratico, la Figura 4 mostra un amplificatore di potenza audio che non è stabile poiché il condensatore di compensazione C2 è troppo piccolo.
La simulazione con PSpice determina erroneamente che questo circuito è stabile, mentre LTspice fornisce il corretto risultato. La netlist utilizzata in ciascun caso è
* Amplificatore di potenza instabile
Q5 N001 N006 N007 0 Q3904
Q7 N001 N007 OUT 0 Q2219A
Q8 OUT N013 N014 0 Q2219A
Q6 N013 N012 OUT 0 Q3906
V1 N001 0 10
V2 N014 0 -10
R11 N012 N014 5K
R14 OUT 0 8
R9 N006 N008 2K
R10 N008 N012 1K
Q4 N006 N008 N012 0 Q3904
Q1 N005 N009 N011 0 Q3904
Q2 N002 N010 N011 0 Q3904
R3 N011 N014 1K
Q3 N006 N004 N003 0 Q3906
R6 N010 0 20K
R7 OUT N010 200K
V3 IN 0 pulse(0 .1 0 5u 5u 50u 100u)
R8 N001 N003 100
R4 N004 N005 10K
C2 N006 N004 10p
R13 N013 N014 1K
R12 N007 OUT 1K
C3 N006 N012 .001u
Q9 N005 N002 N001 0 Q3906
Q10 N002 N002 N001 0 Q3906
R2 IN N009 9.09K
.tran 100u 100u
.model Q3904 NPN(Is=1E-14 Vaf=100 Bf=300 Ikf=0.4 Xtb=1.5
+ Br=4 Cjc=4p Cje=8p Rb=20 Rc=0.1 Re=0.1 Tr=250n Tf=.35n
+ Itf=1 Vtf=2 Xtf=3)
.model Q3906 PNP(Is=1E-14 Vaf=100 Bf=200 Ikf=0.4 Xtb=1.5
+ Br=4 Cjc=4.5p Cje=10p Rb=20 Rc=0.1 Re=0.1 Tr=250n
+ Tf=.35n Itf=1 Vtf=2 Xtf=3)
.model Q2219A NPN(Is=14.34f Xti=3 Eg=1.11 Vaf=74.03
+ Bf=255.9 Ne=1.307 Ise=14.34f Ikf=.2847 Xtb=1.5
+ Br=6.092 Nc=2 Isc=0 Ikr=0 Rc=1 Cjc=7.306p Mjc=.3416
+ Vjc=.75 Fc=.5 Cje=22.01p Mje=.377 Vje=.75 Tr=46.91n
+ Tf=411.1p Itf=.6 Vtf=1.7 Xtf=3 Rb=10)
.probe
.end
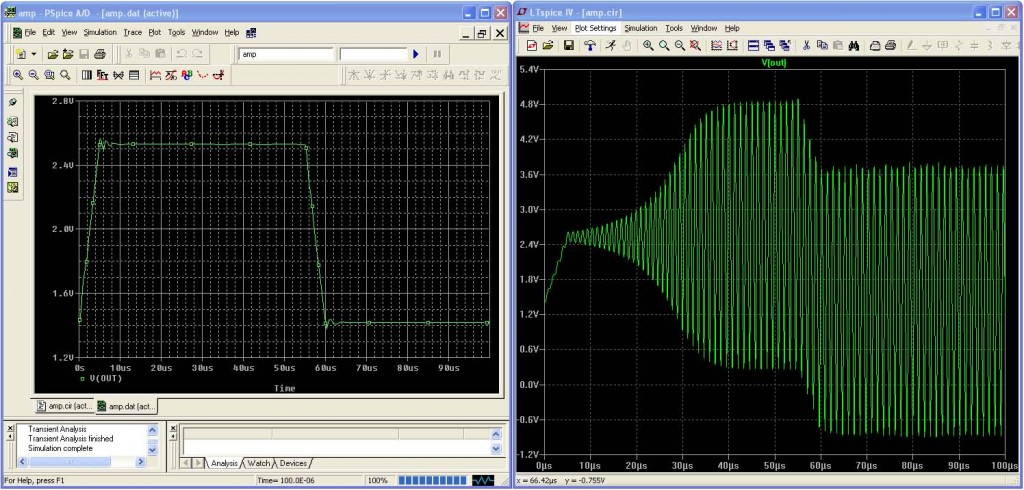
La Figura 5 confronta il risultato erroneo (circuito stabile) di Pspice (a sinistra) con il risultato corretto (circuito oscillante) di LTspice (a destra). La simulazione è un’analisi del transitorio di un segnale di grande ampiezza generato come risposta al gradino. Se nella simulazione PSpice si specifica un incremento temporale abbastanza piccolo, ci si può avvicinare alla corretta soluzione fornita da Ltspice; ciò suggerisce che PSpice sta interpretando le equazioni di dispositivo corrispondenti ai transistor correttamente ma non sta integrando con precisione le equazioni differenziali.
Occorre pertanto un metodo che offra la velocità e precisione del metodo trapezoidale ma senza gli artefatti corrispondenti alle oscillazioni. A tal fine, mentre PSpice elimina le oscillazioni del metodo trapezoidale utilizzando l’integrazione con il metodo di Gear ma costringe a un’accurata selezione dell’incremento temporale adatto, un altro approccio consiste nell’usare una versione “desintonizzata” dell’integrazione trapezoidale affinché le oscillazioni del metodo trapezoidale siano smorzate ma auspicabilmente sia introdotto solo un errore piccolo, accettabile, nel vero funzionamento del circuito. In effetti è possibile, ma non raccomandato, desintonizzare l’integrazione con il metodo trapezoidale di Ltspice mediante l’opzione non documentata trapdamp, aggiungendo l’istruzione SPICE
.options trapdamp=.01
allo schema circuitale. Potrebbe essere possibile individuare un valore di trapdamp che duplica il metodo di integrazione di HSPICEviii. Ciò nonostante, non raccomando l’utilizzo di tale opzione poiché questa smorza l’andamento reale del segnale nel circuito e non è necessaria in LTspice, che ricorre a un metodo migliore per eliminare le oscillazioni del metodo trapezoidale.
LTspice utilizza un metodo di integrazione, il metodo trapezoidale modificato, che offre la velocità e precisione del metodo trapezoidale ma senza gli artefatti corrispondenti alle oscillazioni. Il metodo trapezoidale modificato è stato inventato da Mike Engelhardt alcuni anni fa e inizialmente è stato ampiamente disponibile in Ltspice. Secondo lo stesso autore, è il metodo migliore per integrare le equazioni differenziali di un circuito analogico e non è duplicato in nessun altro programma SPICE; è l’unico metodo che raccomanda per la progettazione di circuiti. LTspice supporta anche l’uso degli altri metodi noti – il metodo trapezoidale e il metodo di Gear – ma semplicemente per consentire di duplicare i risultati erronei ottenuti con altri simulatori SPICE, allo scopo di verificare che i modelli siano interpretati nello stesso modo e che solo il metodo di integrazione sia differente.
Il metodo trapezoidale modificato è stato utilizzato da LTspice per produrre l’andamento mostrato nella Figura 3. Si noti che l’ampiezza delle oscillazioni non varia anche dopo migliaia di cicli, il che dimostra che il metodo trapezoidale modificato di Ltspice non introduce alcuno smorzamento numerico artificiale. Il metodo trapezoidale modificato è stato utilizzato da LTspice anche per produrre l’andamento mostrato nella Figura 5, che mostra come LTspice determini correttamente l’instabilità dell’amplificatore.
Per dimostrare la capacità del metodo trapezoidale modificato di LTspice di eliminare le oscillazioni del metodo trapezoidale, occorre un circuito in cui queste oscillazioni si generino facilmente. Le oscillazioni del metodo trapezoidale iniziano quando l’integrazione del secondo ordine con incrementi temporali discreti non riesce a rappresentare il funzionamento esatto del circuito in un periodo di tempo continuo; possono essere ridotte o eliminate con un controllo attento dell’ordine di integrazione e dell’intervallo temporale.
Poiché da 10 anniix LTspice è il programma SPICE più diffuso, ha simulato un gran numero di circuiti e si è formata una vasta libreria di soluzioni che consentono di evitare le oscillazioni del metodo trapezoidale, per cui non è immediato trovare un controesempio.
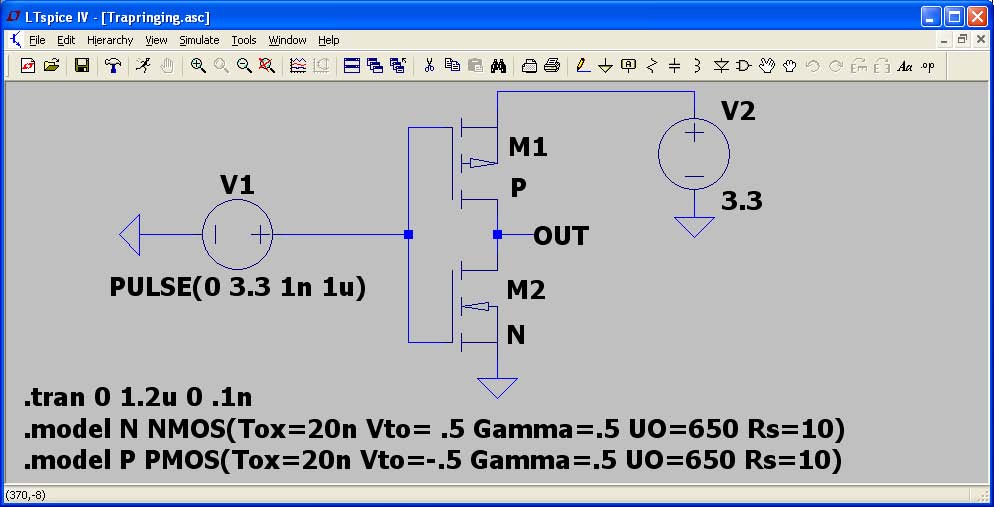
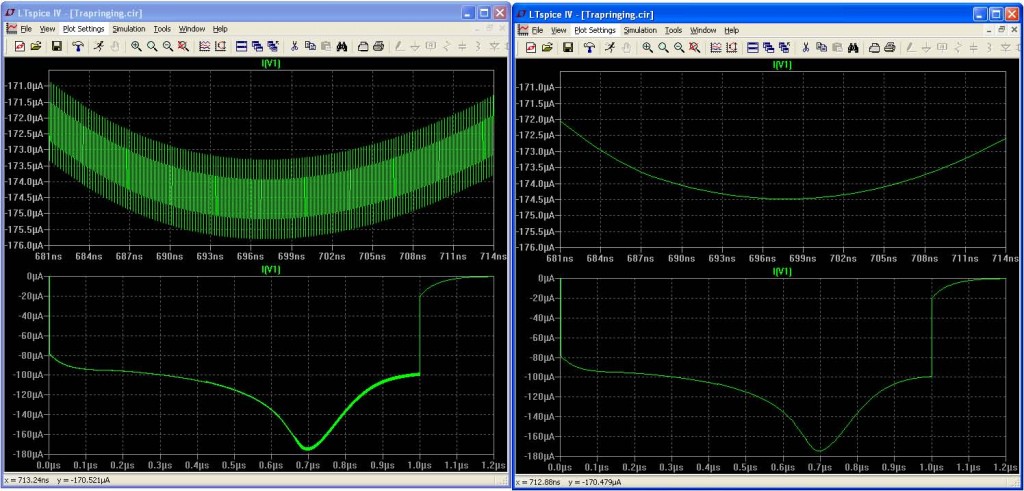
La Figura 6 mostra un circuito che produce oscillazioni del metodo trapezoidale a causa della capacità altamente non lineare dei gate di un inverter a MOSFET dimensionato in modo insolito. Le oscillazioni del metodo trapezoidale sono visibili nella corrente di comando del gate, I(V1).
La Figura 7 confronta l’integrazione con il metodo trapezoidale e quella con il metodo trapezoidale modificato di LTspice. Il grafico superiore rappresenta una regione ingrandita del grafico inferiore, per mostrare chiaramente le oscillazioni. Se si desidera riprodurre questo risultato in LTspice, andare al riquadro SPICE del pannello di controllo e selezionare l’integrazione con il metodo trapezoidale anziché l’impostazione predefinita, ossia l’integrazione con il metodo trapezoidale modificato.
La netlist per questa simulazione è:
* Esempio di oscillazioni del metodo trapezoidale
V2 N001 0 3.3
V1 N002 0 PULSE(0 3.3 1n 1u)
M1 OUT N002 N001 N001 P
M2 OUT N002 0 0 N
.tran 0 1.2u 0 .1n
.model N NMOS(Tox=20n Vto= .5 Gamma=.5 UO=650 Rs=10)
.model P PMOS(Tox=20n Vto=-.5 Gamma=.5 UO=650 Rs=10)
.probe
.end
Tenere presente che la maggior parte dei programmi SPICE non eseguiranno questa serie di istruzioni poiché per questo tipo di MOSFET utilizzano il modello della capacità di Meyer; poiché tale modello non conserva la carica ed è impreciso per canali corti, è diventato obsoleto negli anni Novanta.
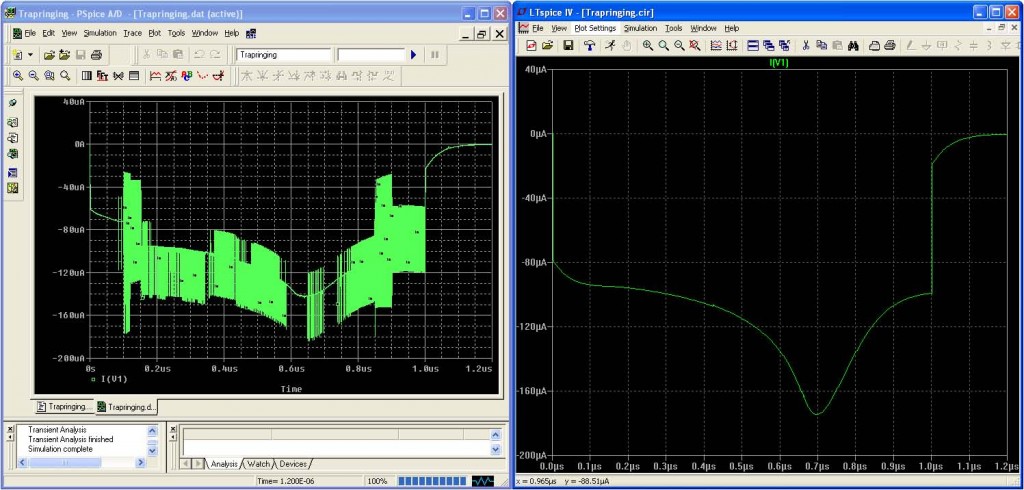
Sia LTspice che PSpice hanno sostituito il modello della capacità di Meyer con il modello della carica di Yang-Chatterjee. Poiché entrambi i simulatori utilizzano le stesse equazioni aggiornate di conservazione della carica, dovrebbero fornire risultati identici. Ma quando si confronta la simulazione PSpice con quella LTspice, come mostrato nella Figura 8, PSpice mostra risultati notevolmente sbagliati.
Tuttavia, le oscillazioni visibili nella simulazione PSpice non sono oscillazioni del metodo trapezoidale poiché non si ripetono da un incremento temporale all’altro e poiché PSpice non usa il metodo trapezoidale. Quasi certamente, questo artefatto è dovuto a un errore nella differenziazione delle equazioni della carica di Yang-Chatterjee per rappresentare le capacità nell’implementazione del modello della carica di Yang-Chatterjee utilizzato in PSpice.
Riepilogo
LTspice non è stata la prima implementazione di SPICE né è l’unica gratuita, ma è la migliore e la più diffusa.
I metodi dell’iterazione di Newton, della matrice sparsa e dell’integrazione implicita sono i metodi numerici fondamentali di SPICE. La robustezza, la velocità e l’integrità dipendono dall’accuratezza con cui questi metodi vengono implementati. Tirate le somme, un simulatore SPICE deve dimostrare al progettista di essere in grado di determinare il corretto funzionamento del circuito e ciò è impossibile se non applica correttamente i metodi numerici fondamentali. LTspice esegue questi metodi correttamente e con maggiore precisione di qualsiasi altra implementazione di SPICE.
Note
i In caso contrario, la soluzione del sistema di equazioni lineari viene utilizza come incremento dell’iterazione: il circuito non lineare originale viene rappresentato con un nuovo sviluppo in serie di Taylor intorno a questa soluzione, anche questa volta troncando lo sviluppo ai primi due termini, e risolvendo quindi il sistema di equazioni lineari simultanee così ottenuto. Il procedimento viene ripetuto finché non si dimostra che è stata trovata la corretta soluzione.
ii PSpice è un marchio di Cadence. Per le schermate si è usata la Versione 9.2.
iii Quanto più sparsa è la matrice, tanto più può essere scritta come se fosse una matrice diagonale, ossia risolta. Poiché le matrici dei circuiti analogici sono così sparse, la decomposizione LU con SuperLU non offre, in relazione alla velocità, un vantaggio così grande come si potrebbe sperare.
iv L’eliminazione delle incognite di una matrice comporta principalmente operazioni di addizione, sottrazione e moltiplicazione. Queste istruzioni richiedono solo tre cicli latenti di clock (occorre eseguire anche alcune divisioni che richiedono molto più di tre cicli di clock, ma è richiesta una sola divisione per incognita da eliminare). L’acquisizione di dati noti solo dall’indirizzo della base che consente l’indicizzazione dura un tempo molto più lungo di tre cicli di clock.
v La letteratura su questo argomento sottolinea che la soluzione numerica non è singolare se viene garantito un incremento temporale sufficientemente piccolo, ma in pratica, un approccio con integrazione esplicita e incremento temporale limitato non funziona a meno che non sia possibile integrare numericamente con precisione infinita. Gli errori non si accumulano sino a un valore infinito poiché vengono arrotondati ma poiché si approssima la derivata con differenze finite campionate. Non esistono efficaci simulatori di circuiti analogici generali che utilizzino l’integrazione esplicita.
vi Saltuariamente SPICE passa all’integrazione del primo ordine, ossia, se si verifica un evento con derivata nel tempo del primo ordine discontinua e nota, come la transizione fra due segmenti rettilinei di una funzione impulsiva o a tratti rappresentativa di un generatore di corrente o di tensione indipendente, la maggior parte delle implementazioni di SPICE passa all’integrazione del primo ordine per le reattanze di tale circuito in corrispondenza della transizione. La versione del primo ordine del metodo di Gear e del metodo trapezoidale è in entrambi i casi un metodo di Eulero all’indietro.
vii Alcuni utenti tendono a essere sospettosi di SPICE poiché la letteratura diffusa denigra il valore della simulazione SPICE.
viii HSPICE è un marchio di Synopsis.
ix LTspice viene scaricato quattro volte al minuto ed è l’argomento di discussione del gruppo più grande di utenti di qualsiasi simulatore. In base al numero di copie distribuite e utilizzate di altre implementazioni di SPICE, ottenute tramite comunicazioni private con rappresentanti delle rispettive aziende che offrono questi altri programmi SPICE, si può affermare che LTspice viene distribuito e utilizzato secondo tre ordini di grandezza in più rispetto a qualsiasi altro programma SPICE.
1. Discontinuità nella curva I-V di un diodo in PSpice (a sinistra) rispetto alla curva I-V continua dello stesso diodo in LTspice (a destra). Le discontinuità influiscono negativamente sulla capacità di un simulatore di risolvere circuiti non lineari.
2. Un semplice circuito la cui soluzione è determinabile tramite esame diretto
3. PSpice (a sinistra), utilizzando l’integrazione numerica con il metodo di Gear modificato, smorza artificialmente ed erroneamente le oscillazioni nel circuito della Figura 2. LTspice (a destra) produce il corretto risultato.
4. Amplificatore di potenza instabile
5. Uscita simulata di un amplificatore di potenza instabile in presenza di un transitorio di notevole ampiezza. PSpice (a sinistra) indica erroneamente che il circuito è stabile, mentre LTspice (a destra) ne rivela correttamente l’instabilità.
LTSpice è disponibile gratuitamente a questo link




Ciao Emanuele,
l’articolo giusto al momento giusto!…
Proprio in questo periodo mi sto avvicinando a questo tipo di programmi..
Ho trovato questo http://everycircuit.com/app che sicuramente non raggiunge il livello di LTSpice, ma ha la grande possibilità di permettere la modifica dei parametri in tempo reale oltre ad avere un’interfaccia eccezionale!
In più è disponibile anche in versione APP per Android e IPhone
Più che un articolo, una dissertazione da concorso per cattedra…
Grazie, Bell’articolo!!! Complimenti!!
Ogni tanto capita che usi Pspice per circuiti semplici. I metodi di integrazione li conosco, però effettivamente non so mai come siano applicati nei programmi. Capita a volte di implementarli in MatLab con non poche difficoltà. LTSpice mi sembra ottimo a riguardo. Lo proporrò al Proff nel corso di conversione statica (elettronica di potenza).
Un risolutore adeguato semplifica l’analisi di un circuito prima della sua realizzazione.
Articolo estremamente interessante.
Io AMO LTspice !
Giovanni
salve molto interessante anche perche sto iniziando ora ad usare il mitico ltspice lunico problema , è l’inglese mà con un pò di pazienza e passione ,lo si capisce comunque!