
Costruiamo un generatore di onda sinusoidale e quadra con sintesi digitale e frequenza da 1 Hz fino a 40MHz con il modulo AD9850, un microcontrollore PIC e un encoder. Con pochi componenti si può realizzare senza troppe difficoltà un generatore che può essere molto utile sia per arricchire la strumentazione di un appassionato di elettronica sia per il radioamatore, infatti, la frequenza generata ha la stabilità e l’accuratezza tipica di un oscillatore a quarzo e può essere usata anche in un apparato radio come VFO (Variable Frequency Oscillator). Da una descrizione teorica del funzionamento della sintesi digitale DDS usata nel chip AD9850, dimostrata anche con un programma di simulazione, si passa alla scelta d’interfacciamento parallelo e al relativo protocollo di comunicazione. In seguito si descrivono la scelta del sistema d’immissione della frequenza da generare, il microcontrollore utilizzato e la realizzazione pratica. Seguono i risultati delle misure effettuate sul prototipo e il listato del programma.
Il circuito integrato AD9850
Il cuore di questo progetto è un interessante chip della Analog Devices: il circuito integrato AD9850 che impiega la sintesi digitale DDS (Direct Digital Synthesis).
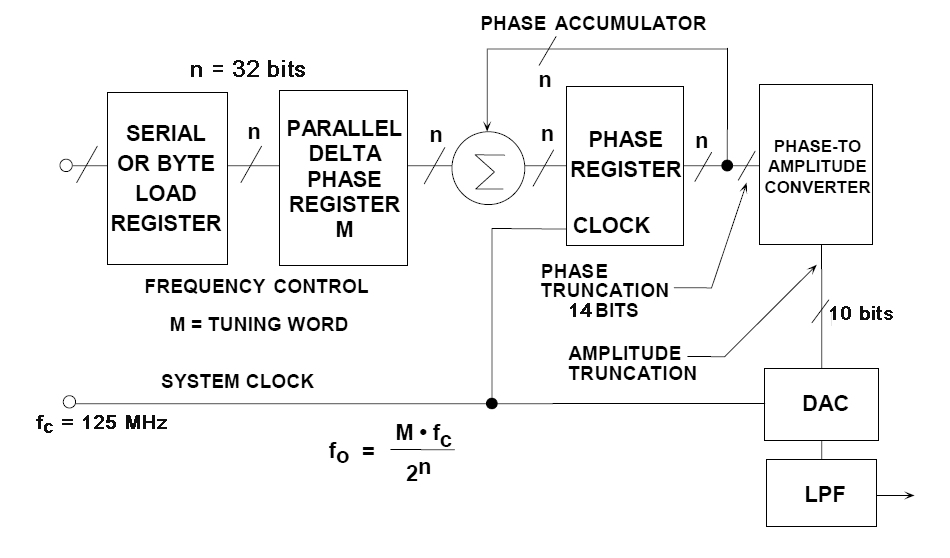
Il circuito DDS, schematizzato in figura 1, è fondamentalmente un divisore di frequenza digitale la cui risoluzione incrementale è determinata dalla frequenza del clock di riferimento diviso per il numero 2n, dove n è il numero di bit della tuning word M (32 bit per il chip AD9850) che serve per impostare la frequenza della sinusoide generata. L'accumulatore di fase (phase register accumulator) è un contatore a modulo variabile che, a ogni clock, incrementa del valore M il numero memorizzato in precedenza in esso. Quando il risultato della somma supera il valore massimo rappresentabile nel registro ( overflow a 2n-1 ), in esso rimane il numero eccedente 2n, permettendo di avere continuità di fase. Il contenuto di questo registro è l’indirizzo che serve per ottenere il valore della funzione seno o coseno per mezzo di una tavola. Per meglio chiarire questi concetti che possono essere di non facile comprensione ho ridotto le cifre a soli otto bit (n=2). Ho poi scritto un programma in Matlab/Octave per realizzare la tavola di 2n =256 valori e per simulare il processo di calcolo anche in forma grafica:
% programma per dimostrare il DDS (n=8 bit) % Giovanni Carrera 12/03/16 M = 1;% delta phase c = 2*pi/255; % conversione in radianti x = 0:255; % ascissa o fase y = sin(x*c); % tavola seno phacc= zeros(1,256);% stati del registro accumulatore for s=1:255 phacc(s+1)=phacc(s)+ M; if phacc(s+1)>=256 phacc(s+1)= phacc(s+1)-256; end; end; plot(x,y(phacc+1),'o-'),grid
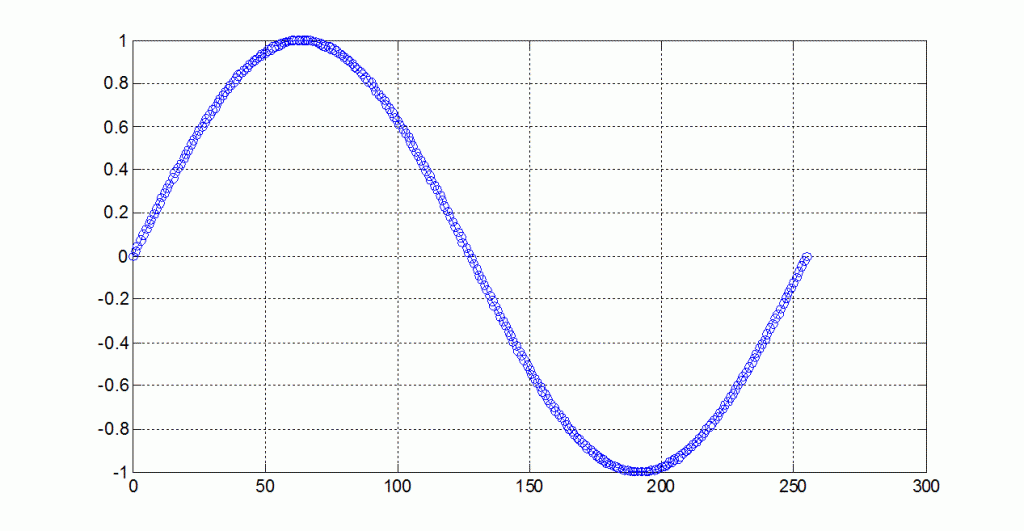
Impostando M=1, si ha un overflow ogni 256 clock. In questo caso l’onda generata ha ben 256 campioni/ciclo, ricavati dalla tavola e la sua frequenza è la minima generabile, come si vede in figura 2.
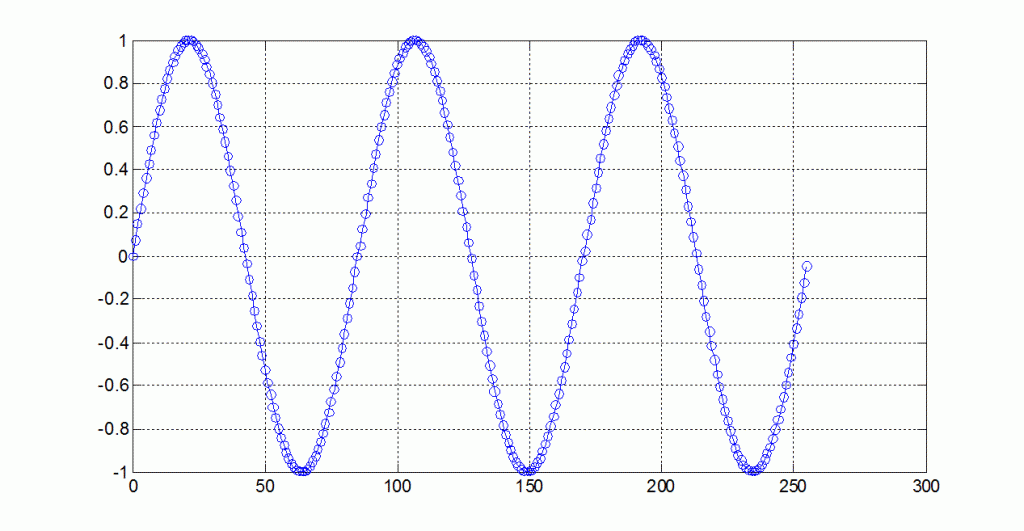
Impostando, nel programma, M=3 si ottiene il grafico in figura 3. Come si vede, c’è una perfetta continuità di fase.
Aumentando M aumenta la frequenza generata e, conseguentemente, diminuiscono i campioni per ciclo. Per il teorema del campionamento di Nyquist occorrono almeno due campioni per ciclo per generare una sinusoide, per cui M deve essere al massimo pari alla metà di 2n, 128 in questo caso. Se volessimo simulare valori alti di M, ossia pochi campioni per ciclo, la rappresentazione grafica non sarebbe di facile interpretazione per via del fenomeno di aliasing grafico. Occorre eseguire un filtraggio digitale per ricostruire le sinusoidi. Più grande è l'incremento aggiunto M, detto anche Δ Phase, maggiore sarà la frequenza in uscita, secondo la formula:
fout = (M× fc) / 2n
Dove fc è la frequenza del clock. Per n=8 e M=3, la frequenza in uscita sarà:
fout = 3× fc/256 = 0,01171875 × fc
Tutto questo sarebbe semplice lavorando a otto bit, a 32 le cose si complicano notevolmente: servirebbe una tavola enorme, per cui occorre troncare a 14 bit in contenuto del registro accumulatore, cosa che crea qualche disturbo di fase ma la risoluzione rimane invariata. Entra in gioco, quindi, un innovativo e brevettato [...]
ATTENZIONE: quello che hai appena letto è solo un estratto, l'Articolo Tecnico completo è composto da ben 3243 parole ed è riservato agli ABBONATI. Con l'Abbonamento avrai anche accesso a tutti gli altri Articoli Tecnici che potrai leggere in formato PDF per un anno. ABBONATI ORA, è semplice e sicuro.







Molte interessante è il paragrafo relativo alle “prove” dove vengono messe in risalto le caratteristiche ma soprattutto eventuali limiti del circuito. Il prototipo ha dimostrato come potrebbe essere interessante costruire il relativo PCB 😉