La modulazione è l'operazione intermedia tra la sorgente d'informazione ed il canale trasmissivo all'interno di un sistema di comunicazione. Con questo articolo diamo il via ad una serie di appuntamenti volti alla comprensione dei principali schemi di modulazione. In questi articoli, oltre alla rappresentazione matematica e grafica dei segnali modulati, verranno presentati anche gli schemi a blocchi dei modulatori/demodulatori, alcuni schemi circuitali e le prestazioni di ognuno rispetto alle risorse fondamentali che guidano il design di questi sistemi, ovvero: potenza, banda e complessità. In questo primo articolo verranno analizzate le modulazioni analogiche di portante analogica, in particolare la modulazione AM (Modulazione d'Ampiezza) ed alcune sue varianti, quella FM (Modulazione di Frequenza) e quella PM (Modulazione di Fase).
Introduzione
Si possono individuare 2 motivi principali per cui si rende necessaria la modulazione di un segnale prima di essere trasmesso su un canale di comunicazione:
- per irradiare i segnali in modo efficiente è necessario che le antenne abbiano dimensioni dell'ordine di un decimo della lunghezza d'onda da trasmettere. Un segnale vocale è di tipo passa basso con frequenze comprese tra 300 e 3400 Hz e quindi lunghezze d'onda tra 106 e 107 metri. Le antenne dovrebbero avere dimensioni chilometriche! La modulazione consente di traslare lo spettro intorno a frequenze elevate rendendo le antenne di dimensioni accettabili;
- la modulazione consente di condividere il canale tra più utenti, utilizzando differenti porzioni dello spettro elettromagnetico.
Introduciamo ora alcuni concetti chiave che torneranno utili nel corso di tutto l'articolo:
- Definiamo segnale modulante, indicato con m(t), il segnale in banda base contenente l'informazione da trasmettere. L'informazione è contenuta nelle variazioni di ampiezza del segnale m(t).
- Definiamo segnale portante, indicato con p(t), il segnale ad alta frequenza il cui scopo è quello di trasportare il segnale modulante. Una delle grandezze fondamentali (ampiezza, fase, frequenza) di p(t) viene fatta variare in modo proporzionale alle variazioni di ampiezza di m(t).
- Definiamo segnale modulato u(t), il segnale ottenuto dopo il processo di modulazione effettuato da m(t) su p(t).
I diversi schemi di modulazione vengono classificati in base alla natura del segnale modulante (analogico o digitale), ed in base alla natura della portante (analogica o impulsiva). In Figura 1 viene riportata una classificazione delle principali modulazioni.
Nella progettazione dei differenti schemi di modulazione occorre tenere presente le tre risorse fondamentali, che sono spesso in contrasto le une con le altre. Tali risorse sono:
- La potenza, particolarmente importante nei dispositivi mobili, poichè più aumentano i consumi, minore diventa la durata delle batterie.
- La banda, spesso limitata a causa della divisione in più canali di un medesimo standard.
- La complessità o costo, ovvero quanto risulta complesso e quindi costoso il ricetrasmettitore.
Per meglio comprendere come queste tre risorse siano legate tra loro iniziamo a discutere nel dettaglio le modulazioni cominciando con la più semplice di esse, ovvero la modulazione d'ampiezza (AM).
Modulazione d'ampiezza
La modulazione d'ampiezza AM è una modulazione analogica di portante analogica. Definiamo la portante p(t) = Ac cos(2πfct + φc), dove Ac rappresenta l'ampiezza della portante, fc la sua frequenza, φc la sua fase. Il segnale modulato u(t) presenterà la seguente espressione:
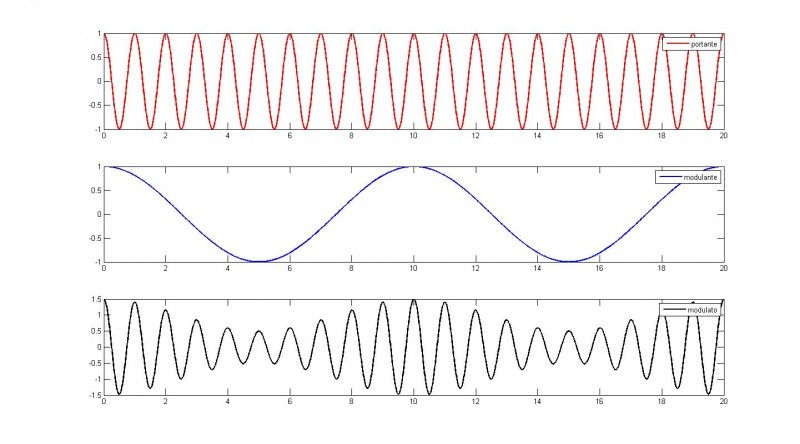
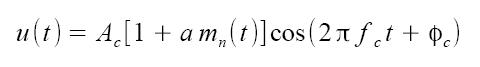 dove mn(t) è la versione normalizzata del segnale modulante m(t), mentre 0 < a < 1 rappresenta l'indice di modulazione. In Figura 2 viene riportato un esempio di segnale modulato AM con indice di modulazione pari a 0.5. Osservando il segnale modulato (in nero) appare evidente come il segnale modulante (in blu) a bassa frequenza, "modelli" la portante (in rosso) ad alta frequenza.
dove mn(t) è la versione normalizzata del segnale modulante m(t), mentre 0 < a < 1 rappresenta l'indice di modulazione. In Figura 2 viene riportato un esempio di segnale modulato AM con indice di modulazione pari a 0.5. Osservando il segnale modulato (in nero) appare evidente come il segnale modulante (in blu) a bassa frequenza, "modelli" la portante (in rosso) ad alta frequenza.
In Figura 3 invece vengono riportati tre esempi di segnali modulati AM con tre indici di modulazione differenti: 0.1/0.5/0.9. L'indice di modulazione non può essere pari o maggiore ad 1, altrimenti si avrebbe distorsione da sovramodulazione.
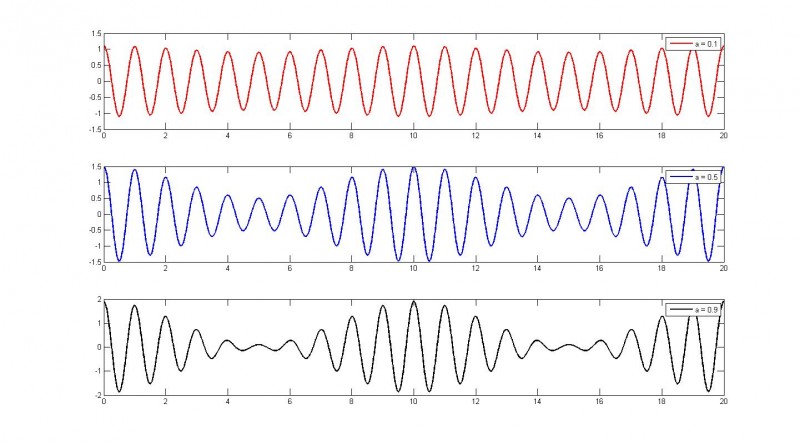
Figura 3: esempi di segnali modulati in ampiezza con differenti indici di modulazione, 0.1(rosso), 0.5(blu), 0.9(nero)
La funzione di auto-correlazione
Vorremmo ora valutare la potenza che la modulazione impiega per trasmettere l'informazione. Il segnale modulante m(t) non è noto a priori, si tratta quindi di un segnale aleatorio. Questo implica che anche il segnale modulato u(t) avrà caratteristiche aleatorie.
Occorrerà operare quindi con grandezze statistiche, come ad esempio la funzione di autocorrelazione Ru(t,τ) = E[u(t)u(t-τ)]. Essa rappresenta la media statistica tra il segnale u(t) e sè stesso dopo un ritardo τ. Per dirla in parole povere ci dice quanto il segnale sia simile in istanti temporali diversi.
Sviluppiamo la funzione di autocorrelazione per un segnale modulato u(t) = m(t) p(t), pari al prodotto tra m(t) aleatorio e p(t)=Ac cos(2πfct + φc):
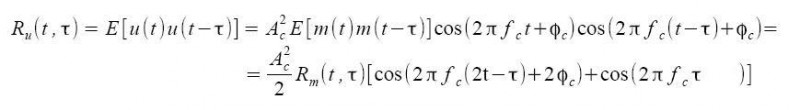 le funzioni coseno escono fuori dalla media statistica poichè sono segnali deterministici, mentre il passaggio alla seconda riga avviene per mezzo della inversa delle formule di prostaferesi, ovvero (cosαcosβ = 1/2 [cos(α+β)+cos(α-β)] ).
le funzioni coseno escono fuori dalla media statistica poichè sono segnali deterministici, mentre il passaggio alla seconda riga avviene per mezzo della inversa delle formule di prostaferesi, ovvero (cosαcosβ = 1/2 [cos(α+β)+cos(α-β)] ).
Rm(t,τ) rappresenta la funzione di autocorrelazione del segnale modulante.
Bisognerà ora passare dall'autocorrelazione statistica a quella media, mediando la prima su tutto l'asse temporale:
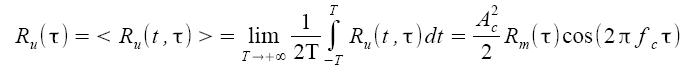 Dall'ultima espressione è possibile valutare la potenza del segnale modulato ed anche la sua estensione in frequenza. La potenza del segnale modulato Pu si valuta ponendo τ uguale a zero:
Dall'ultima espressione è possibile valutare la potenza del segnale modulato ed anche la sua estensione in frequenza. La potenza del segnale modulato Pu si valuta ponendo τ uguale a zero:
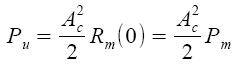 dove Rm(0) = Pm è la potenza del segnale modulante.
dove Rm(0) = Pm è la potenza del segnale modulante.
Per quanto riguarda lo spettro, essendo il segnale aleatorio, non possiamo valutarne la trasformata di Fourier, ma dovremo calcolare la Densità Spettrale di Potenza S(f) (PSD) intesa come trasformata di Fourier della funzione di autocorrelazione media: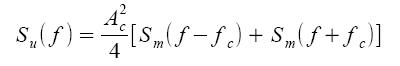 la PSD del segnale modulato Su(f) risulta avere una banda monolatera pari al doppio di quella del segnale modulante Sm(f), come evidenziato dalla Figura 4.
la PSD del segnale modulato Su(f) risulta avere una banda monolatera pari al doppio di quella del segnale modulante Sm(f), come evidenziato dalla Figura 4.
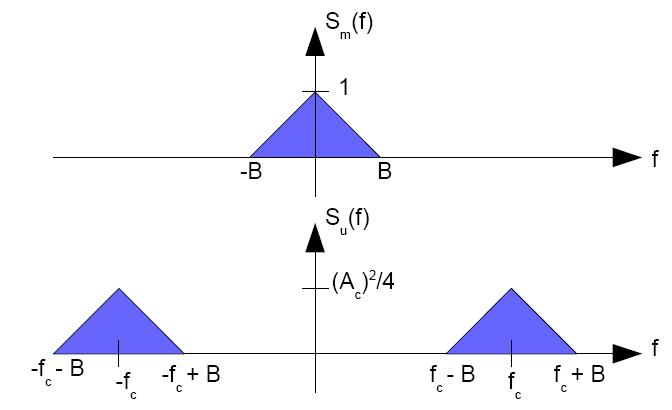
Figura 4: densità spettrale di potenza del segnale modulante (in alto) e del segnale modulato (in basso)
AM convenzionale
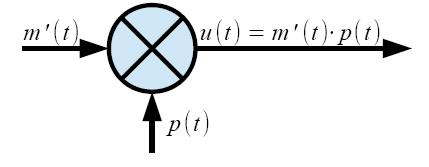
Tornando al nostro caso specifico di modulazione AM, se definiamo m'(t) = [1 + a mn(t)], esso sarà una grandezza sempre positiva per come è definito. Avremo che il segnale modulato può essere visto semplicemente come prodotto tra m'(t) e p(t), come riportato in Figura 5.
Abbiamo così espresso il nostro segnale modulato AM come l'esempio utilizzato per valutare la funzione di auto-correlazione. Possiamo così utilizzare i calcoli già fatti per valutarne la potenza, ma, tenendo presente che il nostro segnale modulante è m'(t) = [1 + amn(t)], quindi Rm'(τ) sarà pari a:
![]() la potenza del segnale modulato Pu sarà quindi data dalla seguente espressione:
la potenza del segnale modulato Pu sarà quindi data dalla seguente espressione:
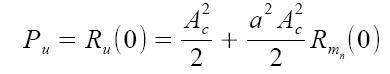 essa risulta composta da due termini, il primo A2c/2 rappresenta la potenza adoperata per trasmettere la portante, mentre il secondo quella adoperata per trasmettere la modulante (segnale utile). Possiamo valutare l'efficienza della modulazione in termini di potenza, come:
essa risulta composta da due termini, il primo A2c/2 rappresenta la potenza adoperata per trasmettere la portante, mentre il secondo quella adoperata per trasmettere la modulante (segnale utile). Possiamo valutare l'efficienza della modulazione in termini di potenza, come:
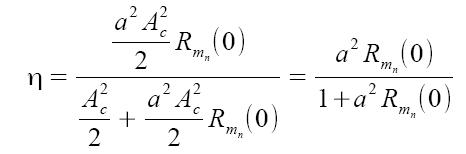 per come sono definiti i parametri risulta che 0 < η ≤ 1/2 e pertanto meno della metà della potenza complessiva viene impiegata per trasmettere il segnale utile.
per come sono definiti i parametri risulta che 0 < η ≤ 1/2 e pertanto meno della metà della potenza complessiva viene impiegata per trasmettere il segnale utile.
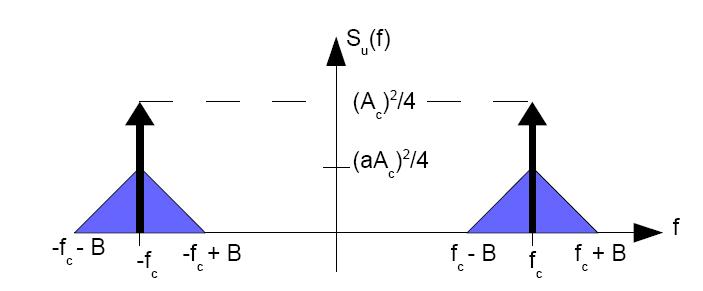
Dal punto di vista dello spettro di frequenze, la PSD è simile a quella del caso visto nel paragrafo sull'autocorrelazione, ma con l'aggiunta di due toni alle frequenze fc e -fc, come evidenziato in Figura 6.
La presenza dei due toni sta ad indicare che la portante in questo tipo di modulazione non è soppressa, come invece avviene in altri schemi di modulazione d'ampiezza che vedremo nel seguito.
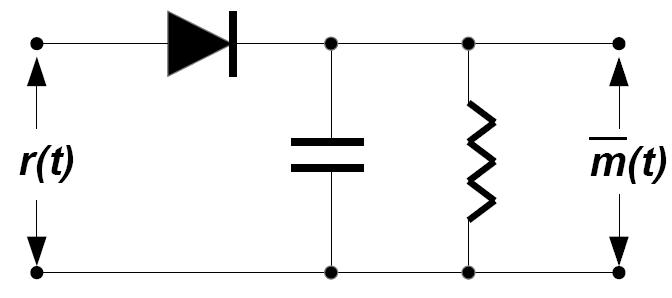
La modulazione AM sicuramente non risulta efficiente in potenza, mentre come efficienza in banda si potrebbe migliorare utilizzando uno schema a singola banda laterale (SSB). Di contro il suo punto forte risiede nella complessità del demodulatore, ovvero un semplicissimo circuito atto a ricavare l'inviluppo del segnale modulato. Tale circuito viene riportato in Figura 7.
Il funzionamento è semplice: quando il segnale ricevuto r(t) genera una tensione che coincide con quella ai capi del condensatore, il diodo conduce e l'uscita insegue l'ingresso. Quando però la tensione d'ingresso scende sotto il valore ai capi del condensatore, il diodo si comporta da circuito aperto ed il condensatore comincia a scaricarsi attraverso il resistore. Scegliendo opportunamente resistenza e capacità, si può imporre una costante di tempo tale da consentire al circuito di ricavare l'inviluppo del segnale.
Modulazioni DSB-SC e SSB-SC
Esistono due varianti alla modulazione AM, che prendono il nome di DSB-SC e SSB-SC. L'acronimo SC sta per suppressed carrier (portante soppressa) e sta ad indicare il fatto che la portante viene soppressa eliminando così la sua richiesta di potenza. L'espressione per il segnale modulato DSB-SC (Double Side Band - Suppressed Carrier) è la seguente:
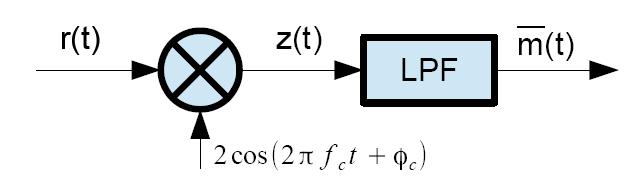
![]() Si può notare che l'espressione per il segnale modulato DSB-SC è uguale a quella utilizzata nell'esempio del paragrafo sull'autocorrelazione. I calcoli già fatti ed i risultati trovati in quell'esempio valgono identici per questo schema di modulazione. Andiamo a visionare lo schema a blocchi del demodulatore DSB-SC, riportato in Figura 8:
Si può notare che l'espressione per il segnale modulato DSB-SC è uguale a quella utilizzata nell'esempio del paragrafo sull'autocorrelazione. I calcoli già fatti ed i risultati trovati in quell'esempio valgono identici per questo schema di modulazione. Andiamo a visionare lo schema a blocchi del demodulatore DSB-SC, riportato in Figura 8:
Si può notare che il demodulatore diviene molto più complesso rispetto al caso di AM convenzionale, infatti, anche se la portante viene soppressa, in ricezione ci sarà bisogno di stimarla per poter effettuare la demodulazione. Il demodulatore DSB-SC, quindi, richiede una "sincronia" con la portante, che invece non è richiesta nell'AM convenzionale. In questo caso si parla di demodulazione "coerente".
[...]
ATTENZIONE: quello che hai appena letto è solo un estratto, l'Articolo Tecnico completo è composto da ben 2837 parole ed è riservato agli ABBONATI. Con l'Abbonamento avrai anche accesso a tutti gli altri Articoli Tecnici che potrai leggere in formato PDF per un anno. ABBONATI ORA, è semplice e sicuro.









Ottima opportunità per ripetere telecomunicazioni. Questo articolo non va solo letto ma va studiato. Interessante come l’autore cura sia la parte teorica e matematica, sia la parte pratica. Interessante la classificazione iniziale di tutte modulazioni e, la tabella finale che mette a confronto le varie modulazioni analogiche.
Gentilissima, grazie
Mitico articolo, ricorda la scuola superiore, gli studi universitari e cose insegnate anche a scuola. Bravi ad averlo pubblicato. Molto utile: rinfresca la memoria e concetti che vanno ricordati.
In effetti dato l’argomento un pò troppo didattico avevo dei dubbi se potesse piacere o meno. Ma dai commenti sembra sia piaciuto
Bello anche lo schema dei quattro quadranti, inserito come figura nell’articolo in oggetto.
Grazie per l’articolo,
preciso e ben fatto compendio che riporta alla memoria quanto studiato diversi anni fa nel corso universitario di Teoria dei segnali.
Molto utile lo schema a quattro quadranti con la panoramica delle modulazioni: se con i prossimi articoli verranno tutte affrontate avrò modo senz’altro di imparare qualcosa di nuovo.
Se posso permettermi un suggerimento sarebbe bello avere anche qualche link a fonti esterne usate, o anche titoli di testi per chi volesse approfondire.
Saluti.
Ti ringrazio. Nei prossimi articoli verrano affronatate le altre tipologie.
Per i testi va bene un qualsiasi testo di “Fondamenti di Comunicazione Elettrica”.
In particolare io ho usato un testo un pò datato ma sempre ottimo:
“Communication Systems Engineering” di Proakis & Salehi
Interessante spiegazione un po complessa per me, ma comunque interessante, io che ho studiato radio tv , non sono dovuto arrivare a queste valutazioni scientifiche cosi approfondite.
Certo al giorno d’oggi la modulazione di frequenza per chi ascolta la radio, ha una qualità maggiore come fedeltà del segnale ricevuto a confronto di un ricevitore AM., che comunque rimane un sistema di ricezione affascinante, in quanto in confronto alla FM si riescono a coprire notevoli distanze, La banda SSB ( banda laterale) è ancora usata oggi dai radioamatori, e come spiegato nell’articolo, è un sistema di trasmissione che non usa un segnale portante, quindi poi nel ricevitore dovrà essere creata una portante per permettere al circuito di rivelare il segnale per poi poterlo ascoltare..
Addirittura se si ha un buon ricevitore in onde corte, si può collegare un BFO al circuito di ricezione per permettere di ricevere correttamente la banda SSB altrimenti risulterebbe incomprensibile,.
Si sta intanto passando alle trasmissioni digitali (DAB) per avere ancora una migliore resa audio, ma per un appassionato di ricezione la AM tradizionale è la banda piu affascinante , perchè ha fatto la storia della trasmissione radio.
Ti ringrazio, ecco link ad articolo sulla DAB https://it.emcelettronica.com/digital-audio-broadcasting-la-radio-digitale