Dopo aver trattato le modulazioni analogiche di portante analogica e quelle numeriche di portante analogica, concludiamo la trilogia di articoli dedicati agli schemi di modulazione, affrontando le modulazioni impulsive. In questo articolo faremo una rassegna delle principali modulazioni impulsive con modulante analogica (PAM, PWM, PPM) per poi passare ad affrontare le fondamentali modulazioni impulsive con modulante numerica (M-PAM, M-PSK, M-QAM, M-PPM). Tutte saranno descritte attraverso i modelli matematici che ne rappresentano lo schema di modulazione, corredate da figure e spiegazioni per rendere la lettura agile anche per i meno esperti. Inoltre, verranno evidenziati i vantaggi e gli svantaggi di ogni schema di modulazione, con comparazione delle prestazioni.
Introduzione
Nelle modulazioni impulsive, un treno di impulsi viene modulato da un segnale analogico che ne modifica i parametri fondamentali. A seconda del parametro modificato si avranno tre tipologie di modulazione:
- Pulse Amplitude Modulation (PAM) dove viene modificata l'ampiezza degli impulsi in funzione dell'ampiezza della modulante;
- Pulse Width Modulation (PWM) dove viene modificata la durata o larghezza dell'impulso;
- Pulse Position Modulation (PPM) dove viene modificata la posizione dell'impulso.
A differenza delle modulazioni analizzate in precedenti articoli, siamo in presenza di modulazioni in banda base, ovvero schemi per i quali il segnale modulato non viene traslato ad alte frequenze per essere trasmesso. Questo tipo di modulazioni si adatta ad essere impiegato in comunicazioni via cavo, quando le distanze in gioco sono contenute, come in una rete locale (LAN) per lo scambio di dati. In tal modo si possono evitare complessità circuitali introdotte dalle operazioni di modulazione e demodulazione. Inoltre, le modulazioni impulsive permettono di accedere al canale trasmissivo con tecniche di tipo TDMA (Time Division Multiple Access), ovvero gli utenti possono condividere lo stesso canale (e quindi le stesse frequenze) in istanti temporali differenti, grazie al fatto che gli impulsi hanno durata temporale finita.
Nel caso di modulazione impulsiva definiremo, quindi, i seguenti segnali:
- m(t) sarà il nostro segnale modulante contenente l'informazione da trasmettere nella sua variazione di ampiezza;
- g(t) sarà un segnale ad energia unitaria, ovvero un impulso. Andremo così a modulare mediante m(t) una successione di impulsi (anche detta treno di impulsi) modificandone uno tra ampiezza, durata o posizione;
- u(t) sarà il segnale modulato generato dalla modulazione.
Pulse Amplitude Modulation (PAM)
Nella modulazione d'ampiezza impulsiva PAM, il segnale modulante m(t) va a modificare l'ampiezza di un treno di impulsi. L'espressione del segnale modulato u(t) è la seguente: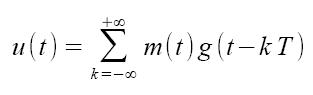 dove T rappresenta l'intervallo di segnalazione. Nella Figura 1 viene riportato un esempio di segnale modulato PAM.
dove T rappresenta l'intervallo di segnalazione. Nella Figura 1 viene riportato un esempio di segnale modulato PAM.
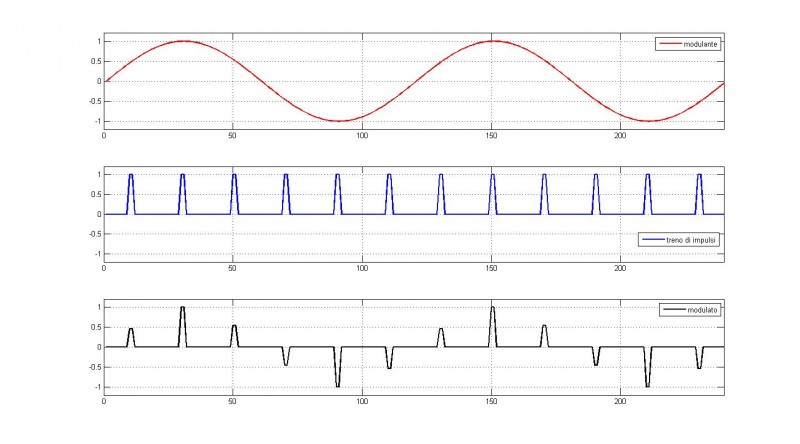
Figura 1: esempio di segnale modulato PAM (in nero) con modulante sinusoidale (in rosso) e portante impulsiva (in blu)
Un vantaggio di un segnale modulato PAM, è quello di richiedere poca larghezza di banda. Tra gli svantaggi, invece, vi è sicuramente la richiesta di una elevata precisione nell'ampiezza dell'impulso, il che la rende maggiormente sensibile al rumore termico.
Pulse Width Modulation (PWM)
La modulazione a larghezza d'impulso è completamente differente dalla PAM poichè sposta la modulazione nel dominio del tempo. Il segnale modulante m(t) va a modificare la durata degli impulsi per mezzo della sua ampiezza. L'espressione del segnale modulato u(t) è la seguente: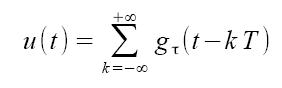 dove gτ(t) rappresenta l'impulso di durata τ. La durata dell'impulso sarà quindi ottenuta dalle seguenti formule:
dove gτ(t) rappresenta l'impulso di durata τ. La durata dell'impulso sarà quindi ottenuta dalle seguenti formule:
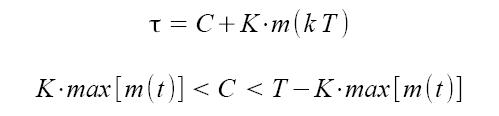 L'unico parametro da scegliere resta K. In Figura 2 viene riportato un esempio di segnale modulato PWM.
L'unico parametro da scegliere resta K. In Figura 2 viene riportato un esempio di segnale modulato PWM.
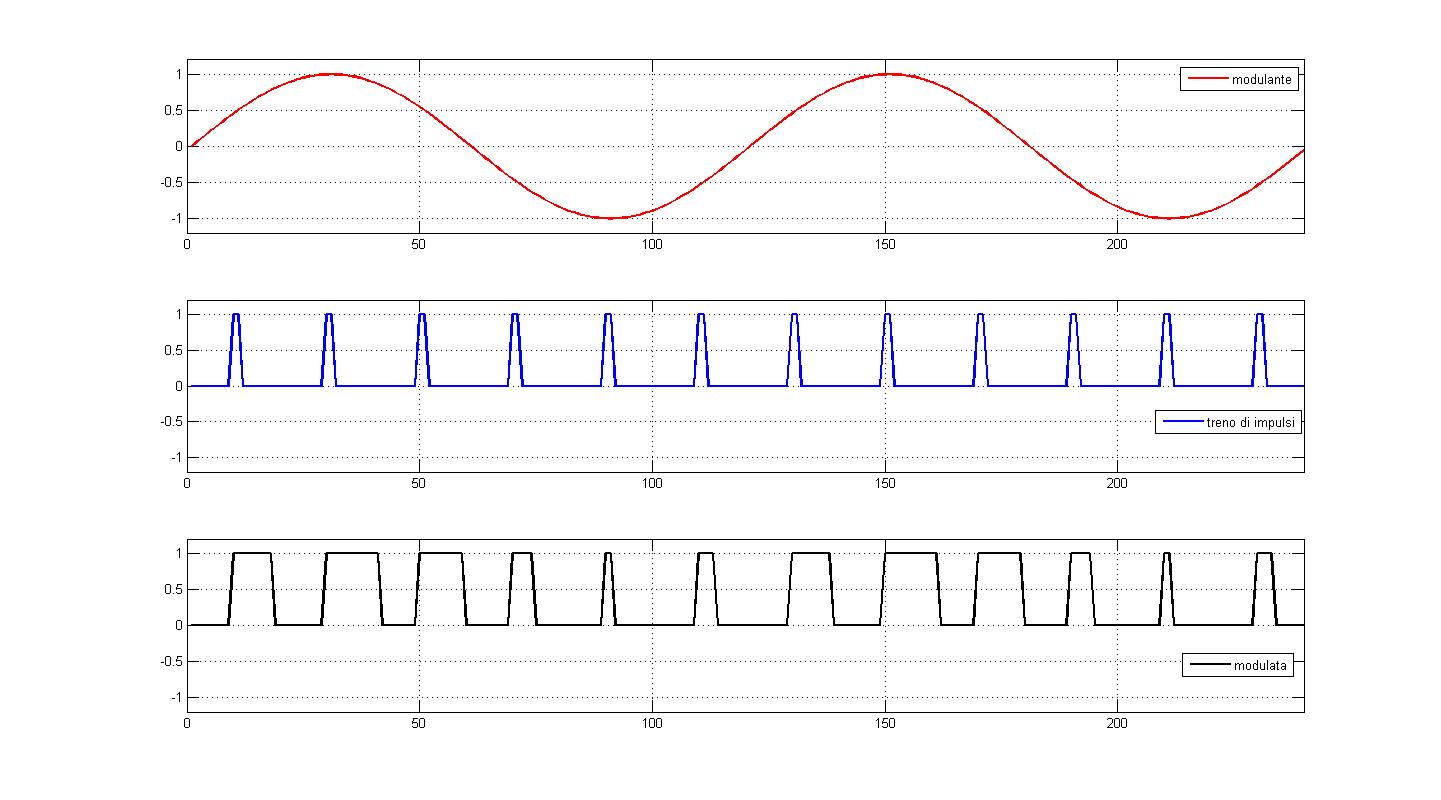
Figura 2: esempio di segnale modulato PWM (in nero) con modulante sinusoidale (in rosso) e portante impulsiva (in blu)
In questa modulazione le richieste in termini di larghezza di banda sono circa un ordine di grandezza superiori a quelle per la modulazione PAM, di contro la durata degli impulsi è facilmente sintetizzabile ed offre maggiore immunità al rumore essendo quest'ultimo additivo in ampiezza e non in durata.
Pulse Position Modulation (PPM)
Nella modulazione a posizione d'impulso, la modulante modifica la posizione dell'impulso all'interno dell'intervallo T, in funzione della sua variazione d'ampiezza. Gli impulsi sono tutti identici in termini di forma (ampiezza e durata). L'espressione del segnale modulato u(t) è la seguente:
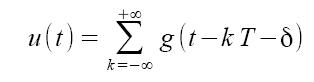 dove δ rappresenta lo spostamento dell'impuslo all'interno dell'intervallo di segnalazione T. Tale spostamento può essere ottenuto dalle seguenti formule:
dove δ rappresenta lo spostamento dell'impuslo all'interno dell'intervallo di segnalazione T. Tale spostamento può essere ottenuto dalle seguenti formule:
La Figura 3 riporta un esempio di segnale modulato PPM.
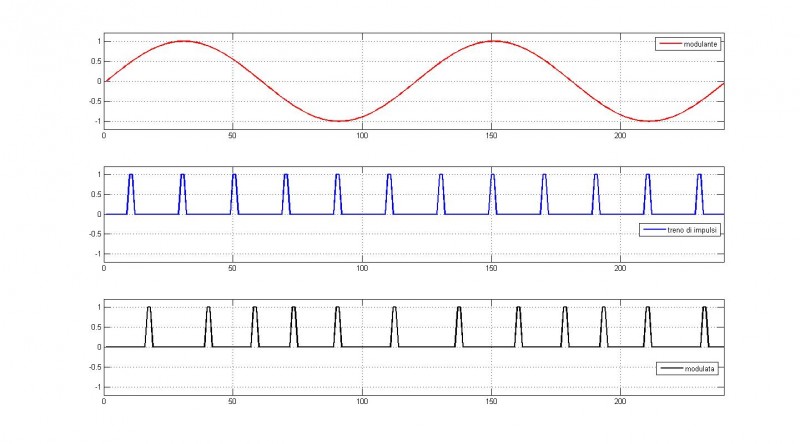
Figura 3: esempio di segnale modulato PPM (in nero) con modulante sinusoidale (in rosso) e portante impulsiva (in blu)
Riprodurre impulsi tutti identici tra loro, rende questa modulazione maggiormente attraente rispetto alle altre. Di contro, l'efficienza in termini di potenza non la rende preferibile alle concorrenti. Riassumiamo pregi e difetti delle tre modulazioni appena elencate nella Tabella 1, inserendo un + laddove la modulazione risulti migliore in quel determinato aspetto rispetto alle altre, ed un - viceversa.
| Modulazione | Efficienza in banda | Efficienza in potenza | Complessità |
| PAM | + | - | - |
| PWM | - | + | - |
| PPM | - | - | + |
Le tecniche di modulazione impulsiva possono essere anche impiegate per trasmettere segnali modulanti che assumono solo un numero discreto di valori, ed essere così adattate ad operare nell'ambito digitale. Andremo nel seguito ad analizzare le più importanti di queste segnalazioni multi-livello.
Modulazione M-PAM
Supponiamo di avere una sorgente binaria che emette ad intervalli di tempo regolari Tb, un 1 logico o uno 0 logico, allora:
- denotiamo con m(k) il simbolo binario emesso nell'istante kTb, con k numero intero;
- una sequenza di h simboli binari emessi viene definita messaggio, con h numero naturale;
- il generico messaggio diventa quindi una realizzazione di un processo aleatorio a valori in {0,1};
- i singoli simboli m(k) rappresentano, invece, variabili aleatorie indipendenti ed identicamente distribuite (iid), ovvero, la probabilità nell'istante kTb di emettere uno 0 logico è uguale a quella di emettere un 1 logico:
![]() Come spiegato in precedenti articoli, i bits in uscita dalla sorgente possono essere raccolti in gruppi di una stessa lunghezza. Se la lunghezza dei gruppi di bits è pari ad h, allora tutte le possibili combinazioni logiche saranno M = 2h. Otterremo, così, un alfabeto costituito da M simboli da associare ai gruppi di bits emessi dalla sorgente. Possiamo allora definire il generico segnale modulato M-PAM come:
Come spiegato in precedenti articoli, i bits in uscita dalla sorgente possono essere raccolti in gruppi di una stessa lunghezza. Se la lunghezza dei gruppi di bits è pari ad h, allora tutte le possibili combinazioni logiche saranno M = 2h. Otterremo, così, un alfabeto costituito da M simboli da associare ai gruppi di bits emessi dalla sorgente. Possiamo allora definire il generico segnale modulato M-PAM come:
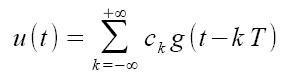 dove ck appartiene all'insieme dei simboli dell'alfabeto e g(t) è il solito impulso ad energia unitaria:
dove ck appartiene all'insieme dei simboli dell'alfabeto e g(t) è il solito impulso ad energia unitaria:
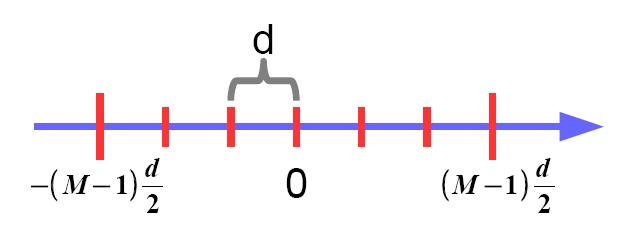
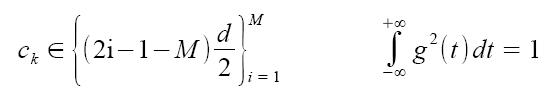 Completiamo le definizioni indicando T = hTb come intervallo di simbolo e d come la distanza tra due simboli consecutivi. Infatti, i simboli dell'alfabeto si possono rappresentare su un asse, contenuti tutti tra gli estremi pari a:
Completiamo le definizioni indicando T = hTb come intervallo di simbolo e d come la distanza tra due simboli consecutivi. Infatti, i simboli dell'alfabeto si possono rappresentare su un asse, contenuti tutti tra gli estremi pari a:
(M-1)d/2 e -(M-1)d/2, e distanti tra loro d. La Figura 4 riproduce questa rappresentazione.
Evitiamo i passaggi matematico - statistici ed andiamo ad esprimere la potenza del segnale modulato M-PAM:
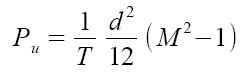 dalla potenza si può ricavare l'energia media per simbolo Εav come prodotto tra Pu e T:
dalla potenza si può ricavare l'energia media per simbolo Εav come prodotto tra Pu e T:
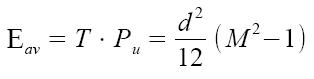 Si tratta di un valore medio di energia rispetto a tutti i simboli che avranno energia diversa l'uno dall'altro.
Si tratta di un valore medio di energia rispetto a tutti i simboli che avranno energia diversa l'uno dall'altro.
Possiamo introdurre anche una versione in banda passante per il segnale M-PAM data dalla seguente espressione:
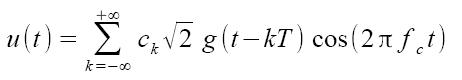 la potenza del segnale resta uguale a quella del PAM in banda base.
la potenza del segnale resta uguale a quella del PAM in banda base.
Riprendiamo per un attimo la modulazione PSK analizzata in un articolo precedente. Possiamo generalizzare tale modulazione per M simboli denominandola M-PSK e rappresentandola mediante la seguente espressione:
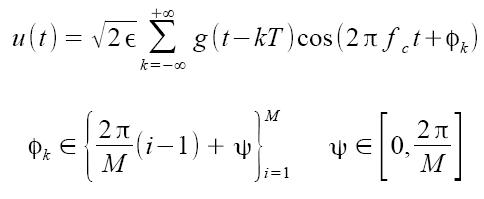 operando sul coseno presente nell'espressione mediante equivalenze trigonometriche, l'espressione diviene:
operando sul coseno presente nell'espressione mediante equivalenze trigonometriche, l'espressione diviene:
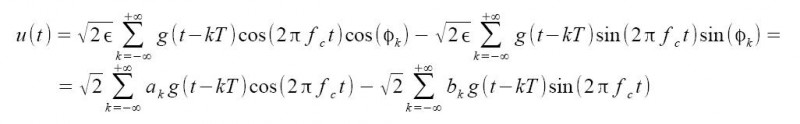 questa nuova formulazione mette in luce il fatto che il segnale M-PSK può essere pensato come la somma di due PAM con portanti in quadratura (sfasate di π/2). I simboli delle due PAM sono dati dai coefficienti ak e bk, rappresentati dalle seguenti espressioni:
questa nuova formulazione mette in luce il fatto che il segnale M-PSK può essere pensato come la somma di due PAM con portanti in quadratura (sfasate di π/2). I simboli delle due PAM sono dati dai coefficienti ak e bk, rappresentati dalle seguenti espressioni:![]() I simboli della PSK sono invece rappresentati nel piano complesso, come punti equidistanti disposti lungo una circonferenza di raggio ( √ε ). Tralasciando i calcoli possiamo comunque affermare che la potenza Pu del segnale modulato M-PSK sarà espressa come:
I simboli della PSK sono invece rappresentati nel piano complesso, come punti equidistanti disposti lungo una circonferenza di raggio ( √ε ). Tralasciando i calcoli possiamo comunque affermare che la potenza Pu del segnale modulato M-PSK sarà espressa come:![]() da cui abbiamo anche ricavato l'energia media. Energia media che è costante, poichè i simboli hanno tutti la stessa energia a causa dell'equidistanza dall'origine del piano complesso. I simboli PAM, invece, hanno energie differenti tra loro, ma allora come è possibile che due PAM in quadratura generino un segnale a simboli equienergetici? La risposta sta nel fatto che i coefficienti ak e bk sono legati tra loro dalla seguente relazione:
da cui abbiamo anche ricavato l'energia media. Energia media che è costante, poichè i simboli hanno tutti la stessa energia a causa dell'equidistanza dall'origine del piano complesso. I simboli PAM, invece, hanno energie differenti tra loro, ma allora come è possibile che due PAM in quadratura generino un segnale a simboli equienergetici? La risposta sta nel fatto che i coefficienti ak e bk sono legati tra loro dalla seguente relazione:![]() quindi non sono indipendenti tra loro ma cooperano per individuare i simboli lungo la circonferenza nel piano complesso.
quindi non sono indipendenti tra loro ma cooperano per individuare i simboli lungo la circonferenza nel piano complesso.
Modulazione M-QAM
La modulazione QAM (Quadrature Amplitude Modulation) è in grado di combinare numericamente le modulazioni di ampiezza e fase. L'espressione del segnale modulato M-QAM è la seguente:
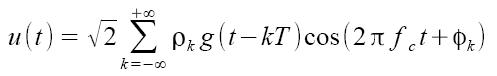 attraverso le relazioni trigonometriche il segnale può essere reinterpretato nel modo seguente:
attraverso le relazioni trigonometriche il segnale può essere reinterpretato nel modo seguente:
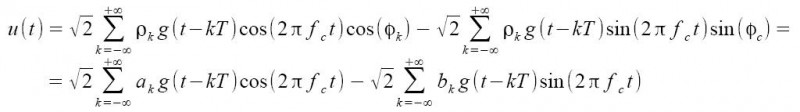 dove per i coefficienti ak e bk valgono le seguenti relazioni:
dove per i coefficienti ak e bk valgono le seguenti relazioni:
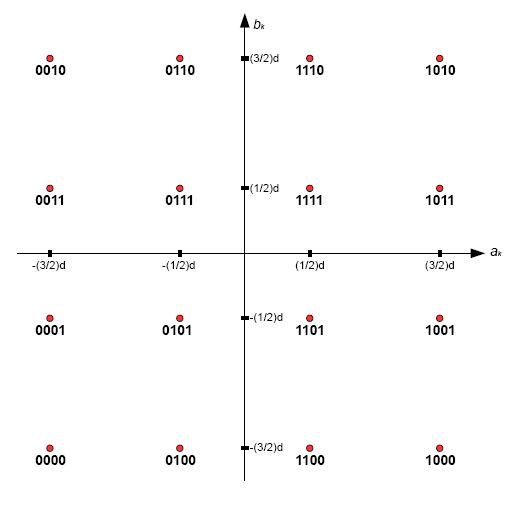
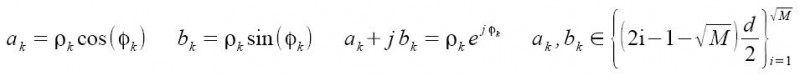 Vediamo adesso un caso particolare di modulazione QAM, con M = 16. Se M è uguale a 16, vuol dire che i simboli dell'alfabeto saranno pari a 16, e ciò implica che ogni simbolo sarà formato da 4 bit. Nella Figura 5 viene rappresentata la cosiddetta costellazione, ovvero tutti i possibili simboli in un riferimento cartesiano (ak, bk).
Vediamo adesso un caso particolare di modulazione QAM, con M = 16. Se M è uguale a 16, vuol dire che i simboli dell'alfabeto saranno pari a 16, e ciò implica che ogni simbolo sarà formato da 4 bit. Nella Figura 5 viene rappresentata la cosiddetta costellazione, ovvero tutti i possibili simboli in un riferimento cartesiano (ak, bk).
Attraverso calcoli che non riportiamo è possibile determinare l'espressione dell'energia media per simbolo di una modulazione M-QAM, pari a:
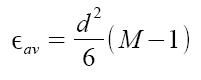 Modulazione M-PPM
Modulazione M-PPM
Nelle precedenti modulazioni il contenuto informativo risiede nei coefficienti (ak,bk,ck), mentre il segnale di energia g(t) è indipendente dal simbolo trasmesso. Un approccio differente è quello di adottare forme d'onda dipendenti dal simbolo trasmesso, indicandole con g(t,ck). L'impulso ad energia unitaria sarà scelto tra M forme d'onda distinte: g(t,ck) ∈ {s1(t),s2(t),...,sM(t)}. Inoltre, è possibile scegliere un insieme di forme d'onda di uguale energia ed ortogonali tra loro, ovvero:
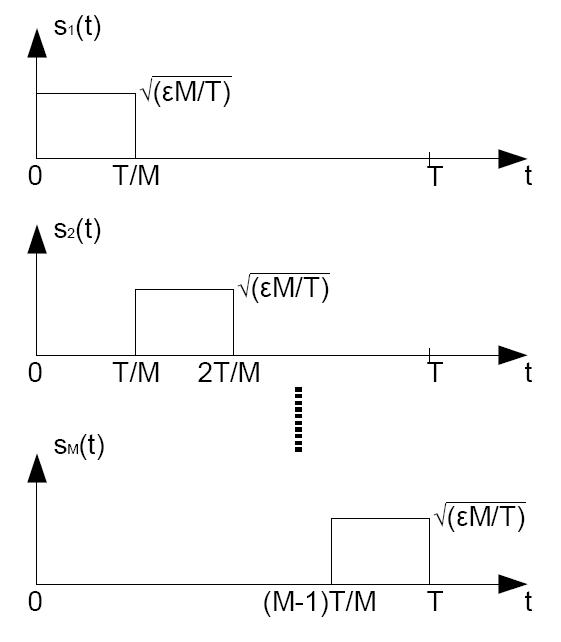
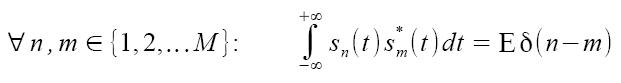 In sostanza se n ed m sono uguali, l'integrale restituirà l'energia dell'impulso altrimenti zero. La modulazione M-PPM rappresenta un esempio di modulazione mediante forme d'onda ortogonali. In tal caso l'ortogonalità è garantita dal fatto che le forme d'onda non si sovrappongono nel tempo, come risulta evidente dalla Figura 6.
In sostanza se n ed m sono uguali, l'integrale restituirà l'energia dell'impulso altrimenti zero. La modulazione M-PPM rappresenta un esempio di modulazione mediante forme d'onda ortogonali. In tal caso l'ortogonalità è garantita dal fatto che le forme d'onda non si sovrappongono nel tempo, come risulta evidente dalla Figura 6.
Demodulazione e Rivelazione
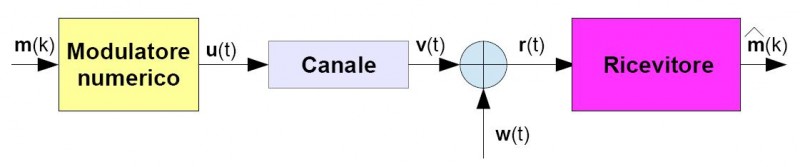
Un sistema numerico di comunicazione può essere sintetizzato come riportato nella Figura 7:
Dove l'espressione di u(t) dipende dal tipo di modulazione impiegata, mentre nel caso di canale ideale avremo che v(t) = Au(t-td), con A definita come l'attenuazione introdotta dal canale sul segnale e td come il ritardo di propagazione nel mezzo. Al segnale v(t) in uscita dal canale si va a sommare il rumore w(t) di tipo AWGN (rumore gaussiano bianco additivo) introdotto dal canale stesso. A questo punto il segnale ricevuto sarà il segnale r(t) = Au(t-td) + w(t), e su questo segnale opererà il ricevitore per ottenere un'approssimazione della sequenza m(k) di simboli trasmessi. Il ricevitore è costituito a sua volta dalla cascata di due blocchi: il demodulatore che effettua la traslazione del segnale in banda base ed un rivelatore che decide tra tutte le sequenze ammissibili quale sia stata trasmessa. In Figura 8 viene rappresentata la cascata di blocchi che forma il ricevitore. [...]
ATTENZIONE: quello che hai appena letto è solo un estratto, l'Articolo Tecnico completo è composto da ben 3104 parole ed è riservato agli ABBONATI. Con l'Abbonamento avrai anche accesso a tutti gli altri Articoli Tecnici che potrai leggere in formato PDF per un anno. ABBONATI ORA, è semplice e sicuro.


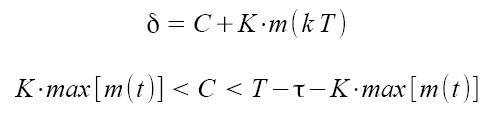





Questa trilogia di articoli è stata molto interessante e ben curata. In quest’ultima parte sulle modulazioni è stato necessario un utilizzo corposo della matematica ma l’argomento è stato spiegato con estrema semplicità. Grazie
Bell’articolo. Ripeto non solo argomenti didattici di tlc, ma interessanti tecnicamente. Bella la parte sulla probabilità d’errore. Grazie della pubblicazione.