
L’articolo tratta alcune questioni di elaborazione numerica dei segnali e i metodi più comunemente adottati per implementare DSPs con i microcontrollori della Microchip.
L’elaborazione numerica dei segnali è una disciplina i cui fondamenti risalgono ai lavori dei matematici del XVII e XVIII secolo, tra cui Newton e Gauss: a dispetto delle sue origini così “antiche”, essa è diventata oggi uno strumento utilissimo in una grande varietà di settori, dall’elettronica all’informatica, dall’ingegneria all’analisi dei dati nella ricerca scientifica.
La sua struttura ha ramificazioni in diverse aree della matematica, dal momento che fa uso di strumenti quali l’analisi complessa, le trasformate di Fourier discreta e veloce, la trasformata Zeta, le convoluzioni, ecc. Gli algoritmi cui essa fa ricorso richiedono spesso elaboratori altamente specializzati per la loro implementazione ed esecuzione e questo ha comportato da un lato uno sviluppo di routine software sempre più sofisticate e performanti e dall’altro la progettazione di circuiti integrati appositi, i Digital Signal Processors (DSPs). L’architettura di questi ultimi viene ottimizzata per realizzare operazioni MAC, saturazioni nelle addizioni o sottrazioni, shift di accumulatori, ecc. Inoltre molti sono dotati di architetture pipeline e di registri e istruzioni dedicate alla realizzazione di buffers circolari per velocizzare l’acquisizione dei dati da processare (vedi i dsPIC della Microchip o i TMS320 della Texas Instruments). L’elaborazione digitale dei segnali ha raggiunto ormai dei livelli di raffinatezza tali per cui è quasi impossibile raggiungere le medesime prestazioni facendo ricorso ai circuiti analogici: essa fornisce poi prestazioni esattamente predicibili, non solo perché consiste nell’esecuzione di algoritmi specifici, ma anche perché è possibile controllare gli errori numerici dovuti alla rappresentazione binaria interna dei segnali.
Elementi di elaborazione numerica
La figura 1 riporta lo schema di un generico sistema DSP: esso acquisisce un certo segnale in ingresso X[t], lo elabora secondo una successione di operazioni matematiche e restituisce in uscita il segnale Y[t].
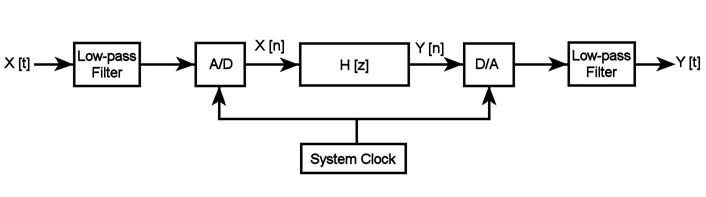
Figura 1: Schema a blocchi di un tipico sistema di elaborazione dei segnali
Per fare questo occorre innanzitutto rappresentare il segnale in ingresso in forma digitale attraverso un ADC e riconvertire quello elaborato in forma analogica tramite un DAC. Occorre qui prestare attenzione a due fatti: innanzitutto, poiché il flusso del segnale analogico in ingresso viene quantizzato e campi onato per ottenere la sequenza X[n], l’intervallo di tempo tra due campioni successivi rappresenta anche il tempo massimo entro il quale l’algoritmo deve essere eseguito dal DSP, altrimenti il segnale in uscita è scorretto, poiché esso deve essere prelevato con il medesimo rate dell’ingresso in tutte quelle applicazioni di real-time processing; d’altra parte il tempo massimo di esecuzione dell’algoritmo non deve eccedere il valore legato al rate di Nyquist; in termini frequenziali ciò significa che il DSP dovrà eseguire l’algoritmo con una frequenza almeno doppia rispetto alla massima frequenza di Fourier presente nel segnale da campionare. In altri termini ciò significa che è necessario limitare tale valore con un opportuno passa-basso (visibile all’inizio della catena di elaborazione), per non avere aliasing: la frequenza di cut-off del filtro dovrà essere tale da eliminare le frequenze che superano la metà della frequenza di esecuzione dell’algoritmo da parte del DSP. I valori campionati sono poi trattati come input di un’equazione alle differenze, legata alla funzione di trasferimento del DSP (H(z)) da un’antitrasformata Zeta. Vediamo di tradurre tutto ciò in modo analitico. Un generico DSP si definisce tecnicamente come un sistema lineare stazionario a tempo discreto e matematicamente quest’ultimo può essere descritto da un’equazione del tipo:
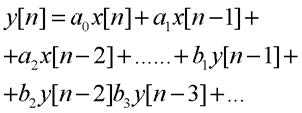
In essa x[n] rappresenta i campioni in ingresso, y[n] quelli in uscita, mentre a e b sono i termini di ricorsione. Da questa relazione è possibile ricavare le caratteristiche chiave del sistema, ovvero la risposta impulsiva, la risposta al gradino, la risposta in frequenza, il diagramma dei poli e degli zeri. In forma più compatta essa diventa infatti:
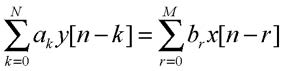
Applicando la trasformata zeta ai due membri della precedente equazione si ottiene
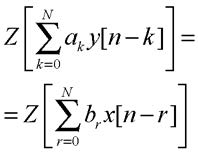
Da quest’ultima, per le proprietà di linearità e di traslazione della trasformata, si ricava
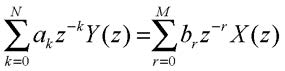
ovvero la funzione di trasferimento nella forma. Questa evidenzia il ruolo assunto dai coefficienti di ricorsione, ma nelle applicazioni si parte generalmente da una funzione di trasferimento in forma fattorizzata del tipo
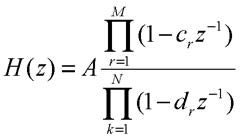
per evidenziare gli zeri e i poli nel piano complesso e dunque le proprietà di convergenza: da queste dipendono la causalità e la stabilità del DSP.
Generazione di toni (DTMF)
Un esempio alquanto interessante di questi concetti consiste nella generazione di toni sinusoidali, ampiamente utilizzati nelle telecomunicazioni per la composizione dei numeri telefonici. E’ infatti possibile ricorrere ad apposite tabelle di campioni della sinusoide per pilotare ad esempio un’uscita PWM, ma questo metodo richiede ampio spazio in memoria per la scrittura dei campioni. Un metodo più efficiente consiste nel passare attraverso una funzione di trasferimento; se vogliamo ottenere dal DSP una sinusoide, si parte dalla trasformata zeta di quet’ultima: essa è del tipo
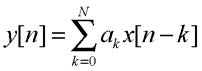
in cui w = 2*PI*f (f è la frequenza della sinusoide) e T è il periodo di campionamento della sinusoide. Vedendo questa come la funzione di trasferimento voluta dal DSP, ovvero H(z) = Y(z)/X(z), allora l’equazione alle differenze corrispondente si può ricavare tramite la trasformata zeta inversa nel seguente modo:
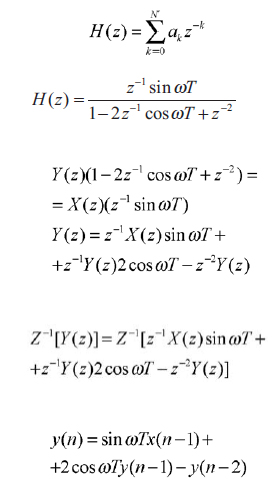
Ponendo a=sinwT e b=coswT, l’equazione si può scrivere come y(n) = ax(n-1) + 2by(n-1) – y(n-2). Si noti come bastino solo due coefficienti per generare la sinusoide: essi contengono infatti sia l’informazione sulla sua frequenza che il periodo di campionamento della stessa. Dando come sequenza di input l’impulso unitario (x(n) = 1 per n=0 e x(n) = 0 altrove) si ricavano i valori in uscita y(n) della sinusoide. Così per i valori negativi di n y(n) e x(n) saranno uguali a zero , per n=1 x(1)=1 e y(1)=a e per n>2 y(n)=2by(n-1)-y(n-2). Si noti anche il fatto che se il periodo di campionamento T della sinusoide è troppo piccolo, allora la frequenza della stessa in uscita non potrà essere molto elevata, dal momento che occorreranno più cicli al DSP per generare la sinusoide. Volendo frequenze più elevate sarà necessaria una maggior potenza di calcolo.
Filtri F.I.R., I.I.R. e regolatori P.I.D.
Riguardando la forma dell’equazione alle differenze generica, si vede come ad essa possano corrispondere due grandi classi di algoritmi: ponendo i coefficienti a=0 si ottengono i cosiddetti filtri F.I.R., a risposta impulsiva finita e risposta in fase lineare, caratteristica questa importantissima in molti strumenti e dispositivi che richiedono bassissima distorsione nella forma d’onda prodotta; se invece almeno uno dei coefficienti a è diverso da zero, allora la risposta all’impulso unitario sarà di durata infinita e si otterranno i filtri I.I.R., dotati di una riproduzione in ampiezza del segnale migliore, ma privi delle qualità riguardanti la risposta in fase. Questi ultimi sono poi di più facile progettazione, a partire dalle specifiche volute (banda passante, di transizione, oscura, ripple) dal momento che esistono formule di progetto in forma chiusa che permettono di derivare la loro equazione a partire dalla corrispondente analogica (vedi la tecnica dell’invarianza all’impulso e della trasformazione bilineare). Essi richiedono un minor numero di coefficienti rispetto alla controparte F.I.R. e quindi un minor dispendio di risorse di memoria. Per esempio un filtro I.I.R. del secondo ordine (i primi due coefficienti a diversi da zero e gli altri uguali a zero) ha una funzione di trasferimento del tipo:
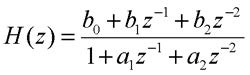
Essa si presenta nella forma che evidenzia i coefficienti: come detto prima esiste anche il tipo fattorizzato che sottolinea la disposizione dei poli e degli zeri. L’equazione alle differenze corrispondente sarà: y(n) = b0x(n) + b1x(n-1) +b2x(n-2) - a1y(n-1) – a2y(n-2). Un’applicazione assai interessante di questi algoritmi ricorsivi consiste nell’implementazione dei regolatori P.I.D., molto usati in campo industriale. La figura 16 riporta lo schema di massima di un tipico regolatore ad anello chiuso: r rappresenta il segnale di riferimento cui va confrontata l’uscita del sistema da tenere sotto controllo, la cui funzione di trasferimento analogica è rappresentata tramite la variabile di Laplace s da G(s).
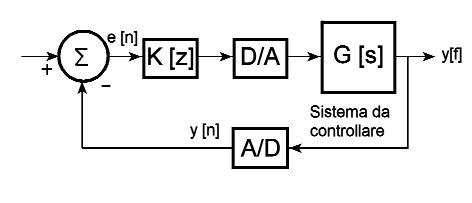
Figura 2: Schema a blocchi di un regolatore P.I.D.
Tale uscita viene campionata dal convertitore A/D, che fa da reazione negativa e chiude l’anello di controllo: il segnale che ne consegue, (y[n]), viene sottratto a quello di riferimento e il risultato costituisce il segnale errore (e[n]), che fa da input al regolatore vero e proprio, la cui funzione di trasferimento discreta è indicata da K[z]; ad essa corrisponde generalmente un filtro I.I.R. e la relativa equazione alle differenze si può ricavare nel seguente modo
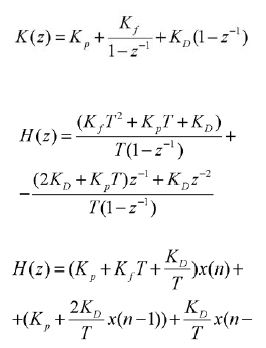
Le azioni proporzionali, derivative e integrali del regolatore sono indicate rispettivamente dai termini contenenti i coefficienti KP, KD, KI. Dal momento che i coefficienti ottenuti possono essere maggiori di uno, essi vanno riscalati per un certo fattore K, in modo da portarli nel corretto formato di rappresentazione dei campioni x(n) e y(n) (solitamente le applicazioni che implementano filtri I.I.R. o F.I.R. ricorrono al formato Qn/I o frazionario in modo che i prodotti rimangano sempre minori di uno).
Alcune caratteristiche hardware dei DsPIC
Come evidenziato dai due esempi precedenti, quello del tono DTMF e quello del filtro F.I.R., le operazioni tipiche effettuate dal DSP sono moltiplicazioni per costanti (i coefficienti del filtro) e addizioni dei prodotti così ottenuti: matematicamente questo significa eseguire la convoluzione lineare tra i coefficienti del filtro F.I.R. (la risposta impulsiva dello stesso) e la sequenza in ingresso (x(n),x(n-1),x(n-2)…); in termini tecnici l’algoritmo processato dal DSP deve eseguire operazioni MAC (Multiply and Accumulate), le quali impongono certe ottimizzazioni all’architettura dei processori più spinti. Esiste infatti una serie di accorgimenti da prendere in considerazione quando si fanno svolgere operazioni di questo tipo da un calcolatore: innanzitutto è necessario scegliere in modo opportuno il formato di rappresentazione dei campioni e dei coefficienti a e b, tenendo conto della propagazione delle incertezze in algoritmi di tipo ricorsivo (round-off error): una precisione semplice a volte non è sufficiente, imponendo la scelta dell’uso di dati a 16 o addirittura 32 bit; pertanto alcuni DSP Microchip (DsPIC) sono dotati di circuiti addizionatori (sottrattori) a 40 bit, in modo da eseguire le corrispondenti opera zioni in un solo ciclo macchina (invece dei 4 richiesti a circuiti a 8 bit). La stessa cosa vale per le moltiplicazioni: i circuiti moltiplicatori sono spesso del tipo 8x8 o addirittura 16x16 (17x17 tenendo conto anche dell’eventuale bit di segno per dati signed). Inoltre la memorizzazione dei risultati intermedi richiede la presenza di registri accumulatori (barrel and shift registers); per non lasciare al programmatore il compito di trattare il problema dello scaling dei risultati intermedi e prevenire dunque casi di overflow o underflow nelle somme/sottrazioni, vanno previsti appositi circuiti di controllo dei bit di segno (questi infatti sono direttamente interessati in caso di overflow nelle rappresentazioni in complemento a due, una delle più utilizzate per trattare operandi con segno). In altri casi si preferisce disporre di un’apposita circuiteria che implementi una logica di saturazione per meglio approssimare somme o sottrazioni il cui risultato esce al di fuori del range di rappresentazione dei dati.
Rappresentazione grafica di un algoritmo F.I.R.
La figura 20 mostra come vengono organizzati nella RAM i coefficienti del filtro e i campioni digitali in ingresso, x[n], per una tipica implementazione di un filtro F.I.R. I vari coefficienti sono puntati dal registro FSR2, mentre il flusso dei dati è indirizzato da FSR0: l’operazione di convoluzione, ovvero l’operazione MAC, consiste in una serie di N moltiplicazioni (dove N è l’ordine del filtro) e N-1 addizioni per il calcolo dell’uscita y[n]. I risultati intermedi dell’algoritmo sono memorizzati nei registri indicati da output_most, output_middle e output_least, i quali saranno rinfrescati dalla somma aggiornata.

Figura 3: Rappresentazione della routine F.I.R.
Dopo ogni moltiplicazione i puntatori vanno aggiornati in modo da indirizzare i nuovi operandi, in modo da realizzare questo schema: il primo coefficiente a[0] viene moltiplicato con l’ultimo sample, il secondo coefficiente con il penultimo e così via. In figura 21 si può vedere l’ordine in cui sono disposti i dati x[n] in arrivo: ogni nuovo sample viene inserito nella posizione inferiore di un buffer lineare di 4 elementi: in questo modo, quando l’I.S.R. relativa alla conversione A/D restituirà il controllo alla routine vera e propria di filtraggio, (e quindi sarà disponibile un nuovo sample in questa posizione), andranno aggiornati tutti i valori del buffer con un’operazione di shift.

Figura 4: Riempimento del buffer puntato da FSR0.




