
Una delle applicazioni elettroniche più importanti, utilizzate e complesse è quella dei filtri. Ecco come realizzare il filtraggio di segnali alle frequenze più varie utilizzando un dsPIC Microchip, al posto dei consueti componenti passivi o degli operazionali esterni.
TEORIA DEI FILTRI PASSIVI
I Filtri Passa Basso
Un filtro passa basso è costituito da un circuito elettronico che permette solo il passaggio di frequenze al di sotto di una data frequenza detta "di taglio". Può essere di tipo attivo o passivo a seconda del fatto che il massimo guadagno possa essere maggiore di uno nel primo caso, o inferiore a uno nel secondo. Si supponga di avere un segnale vocale X (larghezza di banda 30 Hz - 20 Khz ) e di doverlo trasmettere attraverso un canale trasmissivo qualsiasi (doppino telefonico, propagazione per onde e.m.). Usando un processo di modulazione qualsiasi il segnale viene traslato in banda e mandato al ricevitore, il quale dovrà demodulare il segnale per riportarlo in banda base. Ora durante il tragitto effettuato il segnale inviato ha subito delle distorsioni dovute a vari fattori e di conseguenza in ricezione ci ritroviamo un segnale affetto da rumore. Analizzando lo spettro del segnale sarà facile constatare l’introduzione di componenti di rumore aventi proprie frequenze. Attraverso un filtro particolare è possibile eliminare le componenti di rumore dal segnale, dunque, in questo senso, è possibile definire il filtro come un dispositivo in grado di tagliare le componenti di frequenza indesiderate ed attenuare il rumore. Un altro esempio di funzione in cui è utile applicare un filtro passa basso è il filtraggio EMC che si applica nello stadio di alimentazione di una board, al fine di lasciar passare la componente a 50Hz (cioè l’alimentazione 220V) ma non le componenti spurie, di disturbo, a frequenze più elevate. In questo caso esistono degli oggetti ben specifici, che costituiscono ottimi filtri per applicazioni specifiche, realizzati con induttanze e condensatori di precisione calibrati per le diverse esigenze. Il filtro passa basso passivo è uno tra i più semplici filtri da realizzare; esso ha la caratteristica di far passare tutte le componenti di frequenza comprese tra 0 Hz e ft Hz, dove ft è detta frequenza di taglio. Al di là di tale frequenza il filtro elimina le componenti del segnale. Questo filtro è detto passivo in quanto ha come guadagno 0 db (guadagno unitario). Dal punto di vista ideale, un filtro dovrebbe lasciar passare senza modifica le frequenze al di sotto di ft, mentre dovrebbe avere un effetto di eliminazione totale delle frequenze al di sopra di ft. Nella realtà, però, il filtro passa basso non riesce propriamente ad eliminare tutte le frequenze prossime a destra di ft, ma le attenua all'aumentare della frequenza. La caratteristica di questo filtro è quella di avere una funzione di trasferimento del tipo:
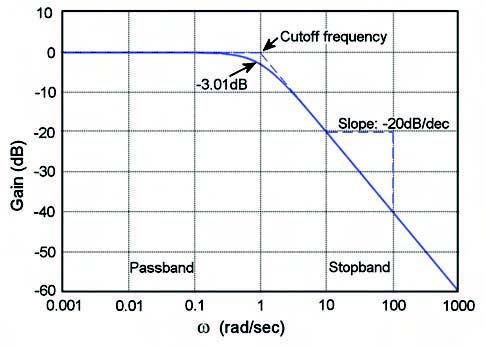
Come si vede si ha la presenza di un polo a denominatore, il quale riduce il modulo della fdt (funzione di trasferimento) di 20 decibel per decade (nei diagrammi di Bode). In figura 1 si presenta l’andamento in frequenza, chiamato altrimenti spettro, di un filtro passa basso, realizzato proprio in un diagramma di Bode.
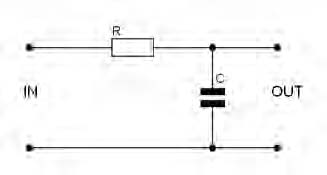
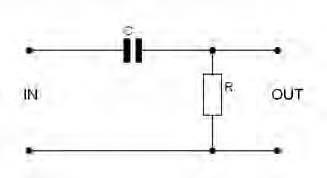
Si noti che le frequenze prossime a 0 vengono passate senza alcuna modifica, cioè sono amplificate di 0dB, mentre invece le frequenze al di sopra di ft sono attenuate in misura sempre maggiore al crescere della frequenza, con una attenuazione di 20 decibel ogni decade. Questo fattore raddoppia al crescere dell’ordine del filtro. L’ordine del filtro altro non è che il numero di poli che questo introduce nella funzione di trasferimento. Nel caso di implementazione di un filtro passivo, come si vedrà, l’ordine del filtro dipende dal numero di squadre RC in cascata. Passando dunque all’analisi implementativa di un filtro passivo di tipo passa basso del primo ordine, si può optare per una “squadra” RC, ossia per un resistore che dal segnale porta al capo positivo di un capacitore e poi all’uscita, come mostrato in figura 2.
Per realizzare filtri di ordine superiore, sarà sufficiente porre in cascata più filtri dello stesso tipo. Per rimanere aderenti ad un caso pratico, si supponga di dover filtrare un segnale spurio di frequenza pari a 2kHz, lasciando invece passare le componenti a 50Hz. Sarà necessario prender mano alla funzione di trasferimento di questo filtro nel dominio delle frequenze. Chiaramente si tratta di un semplice partitore:
Andando ad analizzare il dominio delle frequenze, si nota che il valore di f per cui il modulo di H(f) attenua di 3dB l’ingresso rispetto all’uscita vale f=RC.
Calcolo dei valori per un filtro passa bassoSi debba dimensionare un filtro per la frequenza di 2 kHz. Per prima cosa si sceglierà un valore commerciale di R, che per esempio può essere di 1 kOhm. Da questo si ricava: Una volta trovata questa equazione, il passaggio per il calcolo del valore di capacità è immediato: |
Per questo motivo, fissato un valore di commerciale di R, pari ad esempio a 10kOhm, si ricava il valore di capacità da inserire.
Altri Filtri
Dopo l’analisi effettuata sul filtro passa basso passivo, si passa a descrivere gli altri tipi di filtro, ossia il passa alto, il passa banda e l’elimina banda. Il passa alto è l’esatto duale filtro passa basso. Questo, infatti, non lascia passare le componenti a bassa frequenza, mentre lascia passare tutte le componenti spettrali superiori alla frequenza di taglio ft, con andamento variabile a seconda dell’ordine del filtro. La funzione di trasferimento di un filtro passa alto è la seguente (in figura 3 una sua implementazione):
Oltre al filtro passa alto e al passa basso, che hanno una unica frequenza di riferimento, esistono altre due tipologie di filtro, ossia il passa banda e l’elimina banda, che lasciano passare o eliminano le componenti spettrali di segnali che sono compresi o sono esterni a due date frequenze. Nel caso del passa banda, si ha una banda di frequenza in cui il segnale non viene attenuato. In figura 4 si identificano chiaramente alcuni parametri fondamentali per un filtro passa banda: la banda passante, compresa fra le frequenze ωs1 e ωs2 la attenuazione (Amax) della banda passante rispetto al valore ideale, che sarebbe pari a 0dB; la massima attenuazione di stop band Amin, che si desidera essere il più grande possibile.
Anche per il caso del filtro passa banda si riporta un esempio circuitale in figura 5.
TEORIA DEI FILTRI ATTIVI
I filtri analizzati hanno la comune caratteristica di essere realizzati con componenti passivi. Esistono però altri tipi di filtri, realizzati con componenti attivi, in particolare con amplificatori operazionali, in grado di ottenere risultati molti più raffinati in termini di precisione di frequenza di taglio, immunità alle variazioni termiche e guadagno in banda passante. I filtri attivi vengono realizzati con amplificatori operazionali e reti di reazione RC. Presentando indubbi vantaggi rispetto ai filtri passivi, anche dal punto di vista realizzativo, per semplicità circuitale e di progetto, costo, ingombro, prestazioni, essi predominano nel campo delle basse frequenze e in particolar modo nel settore audio. I limiti principali dipendono dalla necessità di disporre di un'alimentazione in continua e dalla larghezza di banda relativamente poco estesa degli operazionali comuni. Oggi questa limitazione, d’altra parte, diviene sempre meno significativa, dal momento che operazionali a basso costo, come ad esempio i Microchip MCP602x, arrivano a 10MHz di GBPW senza costi particolarmente gravosi. La progettazione dei filtri attivi viene condotta con un procedimento di sintesi che, partendo dalla curva di risposta in frequenza desiderata, definisce la posizione di poli e zeri di una funzione di trasferimento corrispondente e infine determina il circuito che la realizza. Questo processo, valido anche per i filtri passivi, risulta notevolmente agevolato dalle caratteristiche degli amplificatori operazionali, ossia guadagno ad anello aperto AOL ed impedenza di ingresso Ri idealmente infiniti e resistenza di uscita Ro = 0, che consentono di ottenere un guadagno di tensione e potenza in banda passante e che rendono non interagenti fra di loro eventuali celle filtranti in cascata. Come vedremo, proprio questa caratteristica rappresenta un salto tecnologico molto significativo rispetto alle celle passive. In linea generale, ad una curva approssimata, si può fare corrispondere una f.d.t. razionale fratta con n poli ed eventuali m(<n) zeri, scomponibile in un prodotto di f.d.t. di grado inferiore (secondo e primo grado). Il numero n dei poli della f.d.t. definisce l'ordine del filtro. Per meglio esemplificare questi concetti teorici, si prende ora in esame la tipologia di filtraggio più semplice, cioè il passa basso.
I Filtri Passa Basso
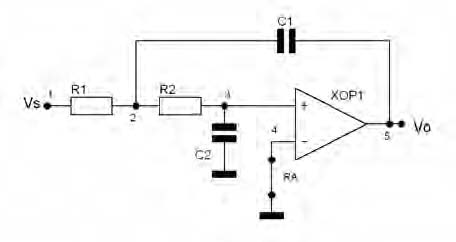
Come per i filtri passivi, anche nel caso degli attivi la tipologia più semplice di filtro è quella di tipo passa basso. Si prende in analisi la più semplice tipologia di filtro attivo, denominata Sallen & Key, dal nome degli inventori di questa cella. Questa tipologia di filtro è caratterizzata dalla modularità, ossia è possibile porre in cascata numerose celle simili per aumentare l’ordine del filtro. In figura 6, un esempio circuitale di cella di Sallen Key.
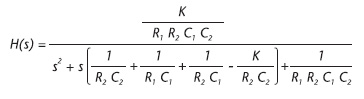
Questa cella presenta una funzione di trasferimento del tipo:
La funzione di trasferimento è di tipo passa basso, poiché al crescere di s, che rappresenta il termine di frequenza, il modulo di H(s) decresce.
Altri filtri attivi
Anche per le altre tipologie di filtraggio, ossia passa alto, passa banda ed elimina banda, la tecnologia attiva offre numerose possibilità. Come per il caso del passa basso, l’elemento con cui si effettuano le operazioni algebriche di somma è l’amplificatore operazionale. Un esempio potrebbe essere costituito dal componente MCP6021 di Microchip, che garantisce una GBPW (Prodotto fra Banda passante e guadagno, che in pratica definisce il livello prestazionale di un opAmp). In figura 7 un esempio di cella passa alto del secondo ordine.
DSPIC E FILTRAGGIO
Innanzitutto è bene ricordare quali motivi possono spingere ad optare per un filtro digitale. Innanzitutto un filtro di questo tipo è meno affetto dal rumore, in quanto la circuiteria non è discreta e non ci sono piste esposte che portano le informazioni filtrate. Anche il consumo di corrente è molto minore, dato che l’assorbimento del micro non varia e non ci sono resistori o altre correnti dovute ad operazionali esterni. Un’altra caratteristica che fa propendere per questi filtri è la dinamicità: con dsPIC sarà infatti possibile variare le caratteristiche del filtro anche a runtime, cosa evidentemente impossibile con filtri a discreti esterni. Un’ultima performance da tenere presente è la mancanza di drift delle caratteristiche con la temperatura e la assoluta mancanza di aging: come è ben noto i condensatori o i resistori con cui sono realizzati i filtri discreti sono soggetti a variazione delle loro caratteristiche in funzione della temperatura di lavoro e del tempo (in un elettrolitico, ad esempio, col passare del tempo l’essiccamento dell’elettrolita interno ne varia il valore). Esistono due tipologie di filtri digitali: i filtri a risposta all’impulso finiti (FIR) e i filtri con risposta all’impulso infinita (IIR). Tramite queste due tipologie di filtro possono essere ricavate tutte le risposte ottenibili dai filtri attivi e passivi già citati in precedenza: Passa Basso, Passa Alto, Passa Banda ed Elimina Banda o Notch. Per quanto concerne i filtri FIR, questi sono caratterizzati da una uscita che, all’istante n, è dipendente dalla combinazione lineare dell’ingresso all’istante n e da T campioni degli ingressi passati. La risposta del filtro ad un impulso è sempre e comunque limitata in valore e nel tempo, ragione questa per la quale questi filtri sono sempre e comunque convergenti. La formula nello specifico è la seguente:
In questa formula T rappresenta il numero di campioni degli ingressi precedenti che contribuiscono a generare l’uscita attuale, nel gergo taps. Chiaramente, maggiore è il numero dei taps richiesti, maggiore sarà la complessità del filtro. Gli elementi bk, invece, sono i coefficienti moltiplicativi dei campioni degli ingressi x[n-k]. Sono proprio questi elementi a determinare il peso, l’influenza che ogni campione degli ingressi precedenti ha sulla uscita attuale. Vi sono varie tecniche di filtraggio, di cui parleremo nel seguito, che consentono di calcolare al meglio questi coefficienti. Si supponga di lavorare con un numero di taps pari a 4. In questo caso la formula da utilizzare sarà la seguente:
Nei filtri IIR, diversamente dai filtri FIR, l’uscita all’istante n dipende dagli ingressi passati e dall’ingresso all’istante n, ma anche dalle uscite passate, fino all’istante n-1. Questo fatto può portare, com’è intuibile, a risonanze che, a fronte di un ingresso impulsivo, danno una uscita il cui valore non converge mai a 0 e può addirittura divergere in valore assoluto. La formulazione in serie di questi filtri è la seguente:
Gli ak sono i coefficienti di feed-back, ossia i coefficienti che combinano i campioni precedenti delle uscite con l’attuale, mentre i bk, come in precedenza, sono i coefficienti di feed-forward, che rendono l’uscita attuale dipendente dagli ingressi passati e dall’ingresso attuale. Quali possono essere i motivi che inducono a scegliere l’una o l’altra tipologia? Dal punto di vista della risposta, un filtro FIR è sicuramente più piatto di un IIR, cosa che lo rende più facile da rappresentare e da controllare. Per quanto riguarda il ritardo di gruppo, ossia la differenza di sfasamento che si ha al variare della frequenza, il FIR si comporta in modo massimamente piatto, cosa che invece non accade per l’IIR. Quest’ultimo, quindi, risulta facilmente distorto in frequenza. D’altro canto, però, un filtro IIR può essere fedele rappresentazione di un filtro analogico, mentre un FIR non può esserlo, proprio per la sua incapacità di esser dipendente dalle uscite passate. Inoltre, il numero di taps richiesti da un filtro FIR è, a parità di risposta richiesta, molto maggiore di un filtro IIR, così come il numero di operazioni matematiche richieste. Chiaramente questo fa sì che la RAM necessaria alla realizzazione di un filtro FIR sia maggiore di quella richiesta per un IIR. D’altro canto, però, è molto difficile avere un errore computazionale in un filtro FIR, mentre invece è facile avere degli overflow implementando un IIR. Dopo aver dunque trattato dal punto di vista teorica le strategie di filtraggio e i diversi vantaggi che si ottengono a seconda delle scelte fatte, si va ora ad implementare queste nozioni nella pratica, facendo uso del software dsPIC Filter Design.
DsPIC Digital Filter Design
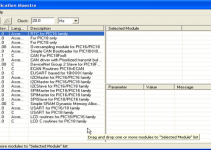
Come anticipato, dsPIC Digital Filter Design è lo strumento indispensabile per il progettista che abbia deciso di realizzare un filtro digitale facendo uso dei dsPIC Microchip. Questo strumento, come la stragrande maggioranza dei tool Microchip, è scaricabile gratuitamente da Internet all’indirizzo www.microchip.com. La versione gratuita ha un numero di TAPS limitati, che però risultano più che sufficienti a realizzare la maggior parte dei filtraggi in applicazioni industriali o consumer. Questo strumento consente di ottenere i coefficienti ak e bk per tutte le tipologie di filtro FIR e IIR discusse in precedenza. Si veda al riguardo la figura 8.
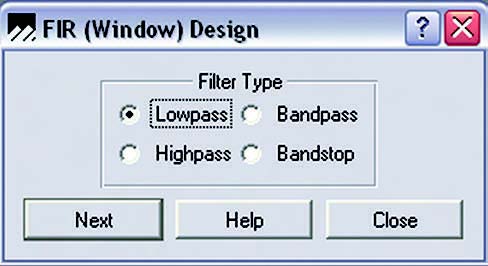
In pratica, all’apertura, il software chiede quale tipo di filtro si desideri realizzare (figura 9).
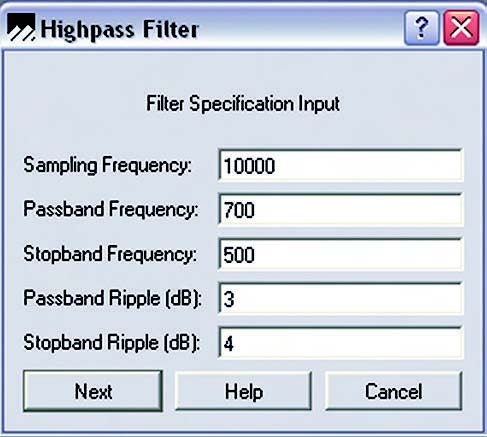
Come esempio si supponga di realizzare un filtraggio FIR di tipo passa alto alla frequenza di 500 Hertz (Stopband Frequency) e di richiedere che la banda passante inizi a 700 Hertz (Passband Frequency). Chiaramente, più stringente è la condizione che si richiede al filtro (più piccola è la differenza fra Stopband e Passband) più difficoltoso sarà generare il filtro, in quanto si richiede una pendenza molto elevata alla transizione fra le due frequenze. Altri parametri da inserire sono poi il ripple massimo richiesto in banda attenuata ed in banda passante. A titolo di esempio si veda la figura 10.
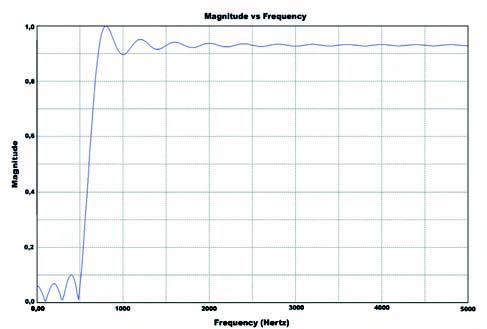
Una volta operata questa scelta, il software propone alcune delle tecniche più conosciute per la finestra di filtraggio, ossia per la vera e propria scelta della tecnica di filtraggio. Fra le più note vi sono la tecnica rettangolare, quella di Hamming, la Gaussiana e la Kaiser. Proprio quest’ultima, per l’esempio considerato, propone una soluzione di filtraggio efficiente con un numero di taps abbastanza contenuto (49 taps). Una volta scelta la tecnica di finestraggio, il software rivela tutta la sua potenza generando alcune forme d’onda, che caratterizzano il filtro. Ad esempio viene generata la caratteristica del filtro in frequenza, altrimenti nota come spettro, come si può vedere in figura 12.
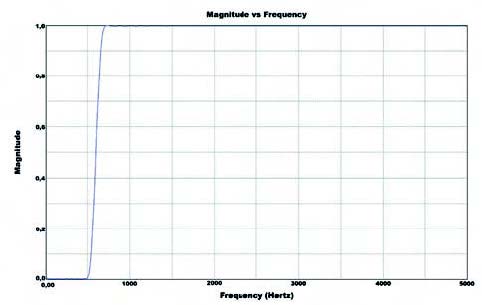
Com’è evidente, questo filtro ha una buona pendenza, ma un ripple residuo in banda passante ed un overshoot abbastanza rilevante della caratteristica. Scegliendo il filtraggio di Hamming, il risultato sarebbe quello di figura 13, migliore del precedente ma a scapito di un maggior numero di taps (165). Chiaramente il trade off sta fra la bontà richiesta e il peso computazionale che si può riservare al filtro.
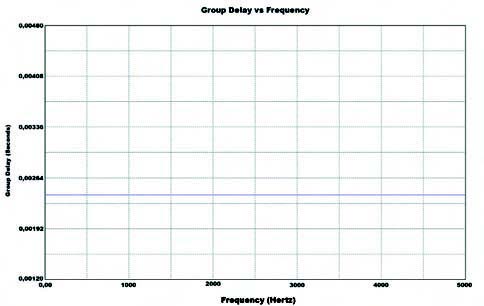
Il software è in grado anche di generare l’andamento in frequenza del ritardo di gruppo. Come detto, nei filtri FIR questo parametro risulta essere massimamente piatto. Il risultato è visibile in figura 14.
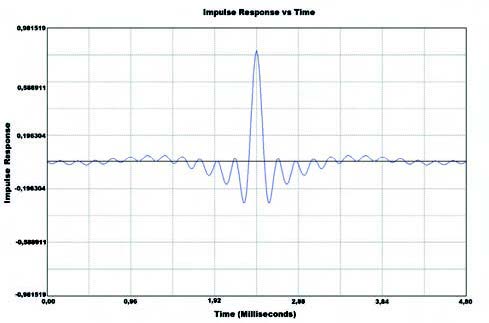
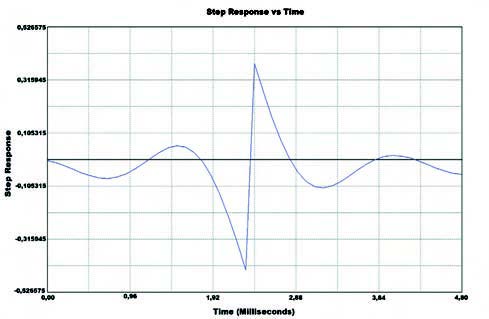
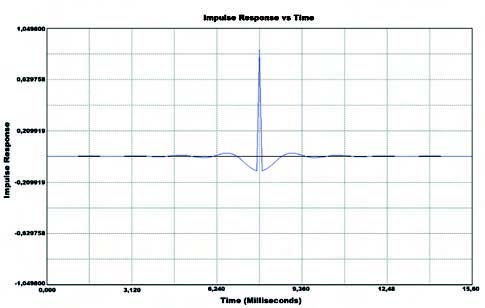
L’analisi fa riferimento al filtro di Kaiser con 49 taps preso in esame. Altre due caratteristiche davvero interessanti sono la risposta temporale del filtro ad un impulso e ad un gradino, visibili rispettivamente in figura 15 e 16.
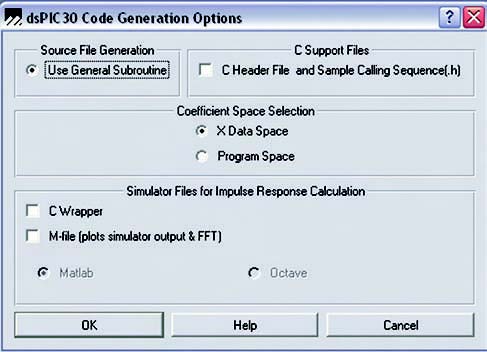
Per finire, il software è in grado di generare i coefficienti del filtro, che saranno poi da includere semplicemente nel progetto, al fine di ottenere il filtraggio progettato. In figura 17 è mostrata la finestra di impostazione della generazione dei parametri.
Nel caso dell’esempio, si sceglie di salvare i dati in RAM, nella X data space. Ecco nel seguito il risultato, sotto forma di codice generato, del filtro considerato nell’esempio. Risultano ben evidenti i 49 taps richiesti in precedenza e la loro allocazione in X Data Space. Il file generato è un Assembly, che può essere incluso in qualsiasi progetto basato su dsPIC Microchip. Nel file sono anche ricordate le diverse chiamate che sono necessarie per la generazione del filtro, come ad esempio la FIRFilterInit. Come visto, in pochi rapidi passaggi si è progettato un filtro per l’analisi evoluta di segnali analogici esterni, facendo uso di tutta la potenzialità di calcolo dei dsPIC, ossia la memoria, il core DSP, gli accumulatori a 40 bit ed il Modulo Circular Addressing, che consente di combinare in automatico i coefficienti e i campioni, consentendo di lasciare completamente libera da ogni calcolo la ALU.
Assembly del filtro Kaiser generato da dsPIC Digital Filter Design
; ..............................................................................
; File esempio.s
; ..............................................................................
.equ esempioNumTaps, 49
; ..............................................................................
; Allocate and initialize filter taps
.section .xdata
.align 128
esempioTaps:
.hword 0xFF6C,0xFEE0,0xFE72,0xFE34,0xFE34,0xFE78,0xFEFE,0xFFBA,0x0097
.hword 0x017C,0x0249,0x02DD,0x031A,0x02E8,0x023A,0x010C,0xFF69,0xFD66
.hword 0xFB24,0xF8CD,0xF68E,0xF495,0xF30B,0xF210,0x68B2,0xF210,0xF30B
.hword 0xF495,0xF68E,0xF8CD,0xFB24,0xFD66,0xFF69,0x010C,0x023A,0x02E8
.hword 0x031A,0x02DD,0x0249,0x017C,0x0097,0xFFBA,0xFEFE,0xFE78,0xFE34
.hword 0xFE34,0xFE72,0xFEE0,0xFF6C
; ..............................................................................
; Allocate delay line in (uninitialized) Y data space
.section .ybss, "b"
.align 128
esempioDelay:
.space esempioNumTaps*2
; ..............................................................................
; Allocate and intialize filter structure
.section .data
.global _esempioFilter
_esempioFilter:
.hword esempioNumTaps
.hword esempioTaps
.hword esempioTaps+esempioNumTaps*2-1
.hword 0xff00
.hword esempioDelay
.hword esempioDelay+esempioNumTaps*2-1
.hword esempioDelay
; ..............................................................................
; ..............................................................................
; Sample assembly language calling program
; The following declarations can be cut and pasted as needed into a program
; .extern_FIRFilterInit
; .extern_BlockFIRFilter
; .extern_esempioFilter
;
; .section .bss
;
; The input and output buffers can be made any desired size
; the value 40 is just an example - however, one must ensure
; that the output buffer is at least as long as the number of samples
; to be filtered (parameter 4)
;input: .space 40
;output: .space 40
; .text
;
;
; This code can be copied and pasted as needed into a program
;
;
; Set up pointers to access input samples, filter taps, delay line and
; output samples.
; mov #_esempioFilter, W0 ; Initalize W0 to filter structure
; call _FIRFilterInit ; call this function once
;
; The next 4 instructions are required prior to each subroutine call
; to _BlockFIRFilter
; mov #_esempioFilter, W0 ; Initalize W0 to filter structure
; mov #input, W1 ; Initalize W1 to input buffer
; mov #output, W2 ; Initalize W2 to output buffer
; mov #20, W3; Initialize W3 with number of required output samples
; call _BlockFIRFilter ; call as many times as needed


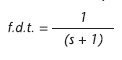
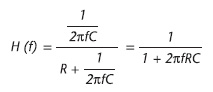

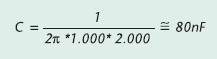
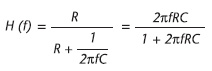



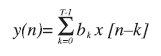

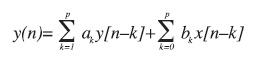



Articolo molto bello.
In pratica, una panoramica su come si “filtrava” nei tempi andati e qualche volta ancora oggi (filtri passivi e successivamente attivi), e come si filtra oggi (DSP).
Un contenuto significativo, oltre che dal punto di vista tecnico, anche da quello storico sulla bella materia che è l’Elettronica e su come essa si evolve nel tempo grazie alla tecnologia dei semiconduttori e ai processi di integrazione sempre più spinti..
Mi viene da fare, oltre i complimenti ad Emanuele, anche una considerazione (un po’ triste) su come, però, si rischi di fare un po’ la fine di certi studenti che hanno praticamente dimenticato (o mai imparato) a fare le radici quadrate perchè usano la calcolatrice da quando frequentano la prima elementare.
E qui mi riferisco a come ormai si progettano i filtri con gli ambienti di sviluppo dei DSP (abbastanza da schiacciabottoni).
Quest’articolo mostra come sia importante (e interessante) tenere sempre presente gli aspetti teorici nelle implementazioni che a volte, per come si effettuano oggi, potrebbero portarci ad essere un po’ come gli studenti che usano sempre la calcolatrice.
Molti tool in ambito di design servono per velocizzare la progettazione incrementando il time-to-market, non vuole essere un modo per nascondere alcune procedure. La teoria e’ importante e in questo articolo viene messa molto bene in evidenza. Senza sapere la teoria e’ impensabile usare i tool di design.