
I dispositivi digitali con i quali interagiamo ogni giorno sono tutti basati sulla logica, o aritmetica, binaria. Computer, smartphone, applicazioni software e app, microprocessori e tutti i componenti realizzati con la tecnologia digitale operano su singole unità di informazione note come bit. Cosa succederebbe se esistesse e utilizzasse una logica di calcolo non binaria, ma piuttosto ternaria?
Introduzione
Nei precedenti articoli abbiamo avuto modo di conoscere IOTA, la moneta decentralizzata nata espressamente per supportare le applicazioni di Internet of Things (IoT) attuali e future. Abbiamo inoltre imparato ad apprezzarne le caratteristiche principali e, soprattutto, i vantaggi offerti da questa criptovaluta, come velocità, scalabilità e assenza di commissioni. Tuttavia, non tutti sono a conoscenza di alcuni aspetti che riguardano l'implementazione di IOTA e l'hardware che gli stessi creatori della moneta intendono realizzare (ci stiamo riferendo a JINN, il microprocessore in logica ternaria di cui parleremo tra poco).
La logica ternaria
Sappiamo come la logica binaria sia basata su due soli simboli (o stati logici): lo 0 e l'1, rappresentabili con un singolo bit. Questi stati logici vengono codificati elettricamente tramite due distinti livelli di tensione, utilizzando ad esempio la logica TTL o un altro standard simile. La logica ternaria, invece, utilizza tre simboli (0, 1 e 2) ed i relativi circuiti hardware che la implementano dovranno essere in grado di gestire tre stati elettrici distinti. Una variante più comoda e interessante della logica ternaria è tuttavia quella che utilizza i simboli 0, 1 e -1, rappresentabili tramite un singolo trit (un trit corrisponde a un bit nella logica binaria). Questa variante, nota come logica ternaria bilanciata, consente infatti di associare alle potenze di 3 dei coefficienti sia positivi che negativi: un determinato numero non è quindi sempre dato dalla somma di potenze di 3 (come avviene nella logica binaria, dove i coefficienti delle potenze di 2 possono valere soltanto 0 oppure 1), ma è possibile anche sottrarre delle potenze. Questo tipo di logica ternaria viene detta "bilanciata" in quanto utilizza coefficienti sia positivi che negativi ed i numeri ternari risultano pertanto "bilanciati" rispetto al punto centrale, rappresentato dallo 0. Facciamo subito un esempio per chiarirci le idee. Supponiamo di voler rappresentare il numero 357 in logica ternaria (d'ora in avanti faremo sempre riferimento alla versione bilanciata):
35710 = 1 x 35 + 1 x 34 + 1 x 33 + 1 x 32 - 1 x 31 + 0 x 30 = 1 1 1 1 ī 03b
dove il simbolo ī rappresenta il coefficiente -1.
Un'importante e utile proprietà della logica ternaria bilanciata è la seguente: per passare da un numero al suo opposto (cioè lo stesso numero cambiato di segno), è sufficiente convertire i coefficienti uguali a 1 in -1 e viceversa, mantenendo inalterati i coefficienti uguali a 0. Infatti:
-35710 = - 1 x 35 - 1 x 34 - 1 x 33 - 1 x 32 + 1 x 31 + 0 x 30 = ī ī ī ī 1 03b
Questa proprietà è molto importante, in quanto la sottrazione si riduce, dal punto di vista computazionale, alla somma (è sufficiente cambiare segno al sottraendo) e pertanto anche il risultante circuito elettronico risulta semplificato. Si osservi inoltre come, per la rappresentazione dei due numeri presi come esempio, siano stati utilizzati un totale di 6 trit. Il numero totale N di valori (positivi, negativi, più lo 0 centrale) rappresentabili con 6 trit è pari a:
N = 3(6-1) x 2 + 1 = 487
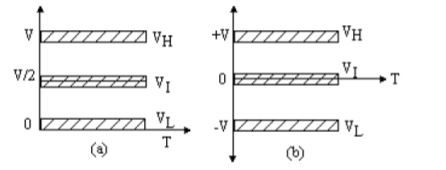
Dal punto di vista elettrico, esistono due possibilità per rappresentare i tre distinti livelli logici su cui si basa la logica ternaria. Entrambe le soluzioni sono indicate in Figura 1. La soluzione a, visibile a sinistra, utilizza tre valori di tensione compresi tra 0 e +V: il livello 0 rappresenta VL (stato logico basso), il livello V rappresenta VH (stato logico alto) e infine il livello V/2 rappresenta VI (stato logico intermedio). La soluzione b, visibile a destra in Figura 1, utilizza invece i livelli -V, 0 e +V per rappresentare gli stessi simboli.
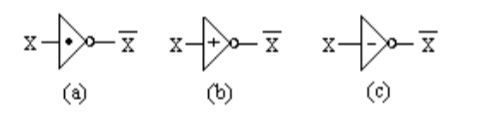
La maggior parte dei sistemi digitali si basa su poche operazioni di base, eseguite indipendentemente dalla complessità del sistema. Queste operazioni di base sono: AND, OR, NOT e il Flip Flop. Nel sistema logico ternario, queste operazioni sono eseguite da una porta ternaria (nota anche come porta T-Logic), l'elemento di base sul quale sono costruiti gli operatori T-AND, T-OR, T-NOT e Flip-Flap-Flop. Consideriamo come esempio l'elemento logico più semplice in assoluto: l'inverter (o NOT). Analogamente a quanto avviene nei circuiti digitali tradizionali, l'inverter ternario è un circuito che fornisce un'uscita invertita rispetto all'ingresso. Poichè però ora l'ingresso può assumere tre valori distinti, nella logica ternaria sono possibili tre tipi di operazioni, come indicato in Figura 2. Più precisamente, le operazioni sono: STI (semplice inverter ternario), PTI (inverter ternario positivo) e NTI (invertitore ternario negativo).
Al di là della sua rappresentazione grafica o circuitale, l'inverter ternario produce un'uscita positiva o negativa se l'ingresso è, rispettivamente, negativo oppure positivo e un'uscita con livello di tensione nullo se l'ingresso è pari a 0. Possiamo sintetizzare questo comportamento mettendo a confronto le tabelle di verità della porta invertente, riferite sia al sistema binario che a quello ternario. Si osservi a questo proposito la Figura 3, in cui la prima colonna indica l'ingresso (A), mentre la seconda colonna l'uscita dell'inverter (not A).
ATTENZIONE: quello che hai appena letto è solo un estratto, l'Articolo Tecnico completo è composto da ben 2252 parole ed è riservato agli ABBONATI. Con l'Abbonamento avrai anche accesso a tutti gli altri Articoli Tecnici che potrai leggere in formato PDF per un anno. ABBONATI ORA, è semplice e sicuro.






L’aritmetica ternaria in una nuova veste per la moneta dell’iot! Non so se un giorno ritorneremo al ternario… 🙂