
Le variabili implicate nell’equazione del radar (per approfondimenti vedi la seguente categoria) mediante la quale viene calcolata la massima distanza di intercettazione di un bersaglio, sono molto importanti nella interpretazione, caratterizzazione e verifica delle performance di un sistema di comunicazione radar. Nel range di misure dei segnali è fondamentale il test dei segnali impulsivi di trasmissione e di ricezione del radar ad impulsi mediante la misura della potenza, della frequenza, dei timing e dell’analisi spettrale. In quest’articolo viene descritto l’utilizzo dello strumento di misura Vector Signal Analyzers (VSAs) e di alcuni strumenti di misura a larga banda, signal analyzers e oscilloscopi, impiegati essenzialmente per le misure di frequenza e fase.
Introduzione
Gli strumenti fondamentali nei test di sistemi radar sono lo Spectrum Analyzer e il Vector Signal Analyzer (VSA). Il primo viene utilizzato dove occorre fare un’analisi spettrale del segnale, quindi nelle misure nel dominio della frequenza; a differenza dello Spectrum analyzer, il vector signal analyzer può effettuare anche misure di ampiezza e di fase nel dominio del tempo, della frequenza e della modulazione. Per meglio comprendere e conseguentemente meglio utilizzare lo strumento vector signal analyzer nelle misure dei segnali dei radar ad impulsi, viene descritta la modalità di funzionamento al suo interno. Per capire il principio di funzionamento di un VSA si può considerare che esso si basa su due concetti: uno originario della teoria delle comunicazioni (Fourier), l’altro dalla teoria del campionamento (Nyquist-Shannon), dando luogo al funzionamento del VSA basato sul calcolo della trasformata di Fourier (FFT). Viene realizzato il campionamento del segnale sotto test, i campioni vengono successivamente passati attraverso un convertitore analogico-digitale, quindi viene memorizzato un blocco di dati contenente un certo numero di campioni digitalizzati del segnale nel dominio del tempo; poi questi dati vengono elaborati mediante il calcolo con FFT ed infine viene reso disponibile il risultato nel dominio della frequenza, ovvero lo spettro di frequenze del segnale. Considerando che per la teoria di Nyquist la frequenza del segnale da sottoporre al campionamento può essere al massimo la metà della frequenza di campionamento, per cui se ad esempio si ha una frequenza di campionamento di 2.048 GHz, la massima frequenza misurabile potrà essere al massimo pari a 1 GHz.
Approfondendo l’argomento
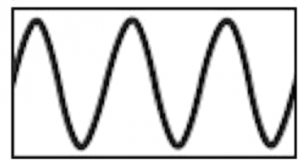
La correttezza di calcolo del segnale con FFT richiede la perfetta ripetitività del segnale in un determinato intervallo di tempo. Questo avviene quando si ha a che fare con segnali CW, impulsi, impulsivi modulati, i quali possono essere considerati ripetitivi sicuramente in un intervallo di tempo come il segnale riportato in figura 1. In questo caso il risultato del calcolo FFT di questa tipologia di segnali non dà luogo ad errori.
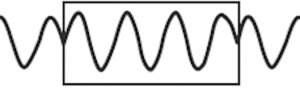
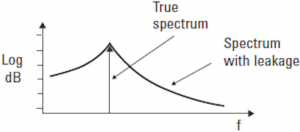
Se invece i segnali sottoposti al calcolo FFT presentano delle discontinuità o semplicemente non possono essere considerati ripetitivi all’interno di un determinato intervallo di tempo, come ad esempio segnali sweept, burst, chirped, allora in questi casi il calcolo con FFT da luogo ad errori. Ciò si traduce nella generazione di frequenze che non rappresentano correttamente lo spettro del segnale che risulta così deformato dall’inserimento di queste indesiderate componenti aggiuntive di frequenze. Questo fenomeno viene definito con il termine “leakage”.In figura 2 un esempio di segnale non ripetitivo o discontinuo nel dominio del tempo, mentre in figura 3 il risultato nel dominio della frequenza del calcolo FFT di un segnale non ripetitivo.
.
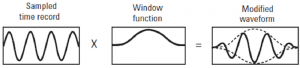
La soluzione per evitare che le discontinuità del segnale possano provocare effetti di leakage, è quella di creare una funzione che forzi al livello zero gli estremi del segnale rilevato all’interno di un intervallo di tempo. Questa funzione è stata definita “Window function”. Nella figura 4 si può osservare che il segnale campionato in un intervallo di tempo sottoposto alla Window funcion risulta modificato con gli estremi forzati a zero con conseguente eliminazione di discontinuità, quindi il segnale viene forzato ad essere di tipo ripetitivo.
Il segnale trattato con la Window funcion presenta una forma d’onda diversa da quella nel dominio del tempo originaria non trattata dalla Window function. Ma questa forma d’onda finale risulta sufficientemente compatibile con la definizione di ripetitività del segnale, conseguentemente sono irrilevanti gli effetti di leakage e il risultato nel dominio della frequenza ha un andamento spettrale conforme con ottima approssimazione ad un segnale di tipo ripetitivo nel dominio del tempo. Nella figura 5 è riportato [...]
ATTENZIONE: quello che hai appena letto è solo un estratto, l'Articolo Tecnico completo è composto da ben 3392 parole ed è riservato agli ABBONATI. Con l'Abbonamento avrai anche accesso a tutti gli altri Articoli Tecnici che potrai leggere in formato PDF per un anno. ABBONATI ORA, è semplice e sicuro.








Quando si lavora con segnali ad alta frequenza è estremamente importante conoscere bene le misure e avere a disposizione gli strumenti necessari. Anche la Rohde&Schwarz dispone di interessanti strumenti per competere nel mercato.
Complimenti per l’articolo, la vorrei contattare in privato per alcune domande ma non trovo il profilo linkedin. Grazie.