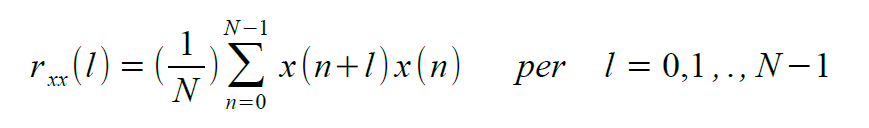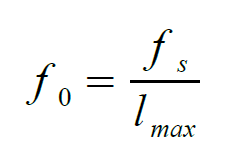
Questo articolo nasce dalla curiosità di riuscire a sviluppare un'applicazione di elaborazione numerica su un hardware limitato dal punto di vista delle risorse. La scheda Arduino Nano 33 BLE Sense, tra i vari sensori disponibili, presenta un microfono MEMS integrato ideale per l'acquisizione audio. Partendo da questa scheda è stata creata un'applicazione in grado di rilevare il pitch, la frequenza fondamentale, della voce umana. La particolarità dell'applicazione, che la distingue da altre implementazioni simili, sta nel fatto che il rilevamento del pitch non avviene nel dominio del tempo, ma per mezzo della funzione di autocorrelazione.
Introduzione
Il comportamento acustico dei suoni emessi quando parliamo è periodico a causa della vibrazione delle corde vocali. La frequenza di oscillazione (frequenza fondamentale), relativa ad ogni suono emesso, è nota come pitch o altezza e dipende dalle caratteristiche fisiche dell'apparato vocale. Ad esempio, la frequenza fondamentale dell'onda sonora relativa alla lettera 'a' varierà da persona a persona, ma resterà comunque all'interno di un intervallo limitato di frequenze. La metodologia utilizzata per determinare l'altezza di un segnale vocale discreto, che descriveremo nell'articolo, è la funzione di autocorrelazione. La funzione di autocorrelazione, è uno strumento utile per l'analisi dei segnali. In generale, la correlazione tra due variabili significa che se si conosce il valore di una, si hanno delle informazioni sull'altra.
Funzione di autocorrelazione
I segnali rappresentano spesso misurazioni di quantità che variano nel tempo. Ad esempio, i segnali sonori rappresentano misure di tensione (o corrente), che corrispondono alle variazioni della pressione atmosferica che percepiamo come suono. Misure come questa presentano quasi sempre una correlazione seriale, cioè una correlazione tra ogni elemento e il successivo (o il precedente). Per calcolare la correlazione seriale, possiamo spostare un segnale e quindi calcolare la correlazione della versione spostata con l'originale. L'autocorrelazione dei segnali periodici permette di stimare l'altezza (frequenza fondamentale) in un determinato momento. La FFT potrebbe sembrare la soluzione migliore, ma su sequenze brevi la risoluzione in frequenza della trasformata tende ad essere scadente. Potremmo ottenere una migliore risoluzione in frequenza prendendo un segmento più lungo (sempre che ciò sia possibile), ma poiché l'intonazione può subire variazioni nel tempo, è possibile che la stima sia affetta da "sfocatura di movimento". Possiamo invece stimare l'altezza in modo più accurato usando la funzione di autocorrelazione. Se x(n) è una sequenza di valori definita su N valori discreti, allora la funzione di autocorrelazione rxx(l) viene calcolata come:
Anche la funzione di autocorrelazione sarà una sequenza definita su N valori discreti. La sequenza x(n) ci aspettiamo sia la versione campionata di un segnale analogico s(t) con frequenza di campionamento fs. In Figura 1 viene riportato il grafico di un segnale sinusoidale e della funzione di autocorrelazione ad esso associata.
Come si può notare, se un segnale è periodico allora:
- L'autocorrelazione avrà un picco all'inizio, quando il ritardo l è uguale a 0. Questo perché il segnale e la copia ritardata sono perfettamente sovrapposti.
- Man mano che il ritardo aumenta, il valore dell'autocorrelazione diminuisce fino ad un minimo che corrisponde alla sovrapposizione del segnale con la sua copia in controfase.
- Quindi, l'autocorrelazione ricomincia ad aumentare fino ad incontrare un nuovo massimo relativo in corrispondenza della nuova sovrapposizione in fase. Il nuovo massimo relativo non ha valore 1 perché, rispetto al valore iniziale, quando i segnali erano perfettamente sovrapposti, essendo la sequenza finita, non tutti i campioni contribuiscono alla sommatoria man mano che il ritardo aumenta.
- Ogni nuovo massimo relativo si avrà ogni volta che il ritardo diventa multiplo del periodo della sinusoide. Quindi la distanza che intercorre tra 0 e il ritardo lmax relativo al primo massimo è proporzionale al periodo della sinusoide.
Da queste osservazioni possiamo ricavare, in maniera euristica, la relazione che lega i valori della funzione di autocorrelazione e la frequenza di campionamento fs. In particolare, abbiamo che la frequenza fondamentale f0 del segnale sarà uguale a fs diviso il ritardo lmax.
Sfrutteremo quindi questa proprietà nella nostra applicazione, ma prima introduciamo il dispositivo con cui andremo a operare.
Arduino Nano 33 BLE Sense
Sul sito web di Elettronica Open Source, la scheda Arduino Nano 33 BLE Sense (Figura 2) è stata utilizzata in molti progetti e quindi rimando il lettore che volesse sapere di più, ai link degli articoli dove la scheda viene descritta in profondità.
In questo articolo, ci focalizzeremo invece sugli aspetti audio della scheda, ovvero sul microfono MEMS MP34DT05 di STM. Si tratta di un microfono MEMS digitale ultracompatto, a basso consumo e omnidirezionale; costruito con un elemento di rilevamento capacitivo e un'interfaccia IC. L'elemento di rilevamento è in grado di rilevare le onde acustiche, ed è realizzato utilizzando un processo specializzato di microlavorazione del silicio dedicato alla produzione di sensori audio. L'interfaccia IC è prodotta utilizzando un processo CMOS che consente di progettare un circuito dedicato in grado di fornire esternamente un segnale digitale in formato PDM. La sigla PDM è l'acronimo che sta per modulazione a densità di impulsi. Questo formato è differente dal classico PCM, comunque non è necessario, ai fini dell'articolo, studiare in profondità questo tipo di modulazione. Ci basta sapere che esiste una libreria denominata PDM.h che ci consente di utilizzare i dati provenienti dal microfono della scheda. La libreria verrà descritta nel capitolo sulla descrizione dello sketch.
Sketch
Per quanto riguarda il rilevamento accurato della frequenza, ci sono molti ottimi esempi di progetti che cercano di risolvere questo problema. Quasi tutti però, usano delle tecniche nel dominio del tempo come Zero-Crossing, Peak Detection, Slope Detection, ecc.. Il nostro approccio, invece, calcola in tempo reale la funzione di autocorrelazione e quindi la frequenza fondamentale, del segnale acquisito. Suddividiamo lo sketch e andiamo a descriverlo pezzo per pezzo.
#include <PDM.h>
L'unica libreria che ci serve è la libreria PDM.h che ci consente di utilizzare il microfono presente sulla scheda Arduino.
static const char channels = 1; static const int frequency = 16000;
Definiamo quindi due parametri che sono il numero di canali audio (1 per mono e 2 per stereo) e la frequenza di campionamento in Hz.
// Buffer to read samples into, each sample is 16-bits short sampleBuffer[512]; // Number of audio samples read volatile int samplesRead=0;
Per poter leggere i dati provenienti dal microfono costruiamo un buffer da 512 byte, e lo denominiamo sampleBuffer. Essendo che ogni campione è stato quantizzato con 16 bit (2 byte), allora il buffer potrà contenere al massimo 256 campioni. La variabile samplesRead servirà per tener conto del numero di campioni letti.
ATTENZIONE: quello che hai appena letto è solo un estratto, l'Articolo Tecnico completo è composto da ben 2268 parole ed è riservato agli ABBONATI. Con l'Abbonamento avrai anche accesso a tutti gli altri Articoli Tecnici che potrai leggere in formato PDF per un anno. ABBONATI ORA, è semplice e sicuro.