
Continua il corso dedicato agli Aeromobili a Pilotaggio Remoto (APR). Siamo partiti illustrandone la tecnologia, i principi di funzionamento, lo stato dell'arte e la storia. Ci focalizzeremo, ora, sui simulatori di scenari, impiegati per testare il comportamento del singolo o di una flotta di velivoli prima dei test sul campo, analizzando quanto messo a disposizione dall'ambiente di calcolo numerico Matlab®, per poi citare e descrivere le peculiarità degli ambienti più diffusi (sia open che closed source). Inoltre, saranno presentati i sistemi di riferimento necessari per definire nello spazio lo stato del drone. Per concludere, analizzeremo cos'è un sistema di riconoscimento e la loro importanza sugli APR, introdurremo l'idea di visione artificiale ed object detection. Si consiglia vivamente di seguire cronologicamente le lezioni che seguiranno, senza fretta ed impazienza nel terminare subito il corso, ma con la consapevolezza di maturare i concetti presentati gradatamente nel tempo.
Introduzione
Per la simulazione di un contesto quanto più simile alla realtà, sul quale poi testare algoritmi per la detection (rilevamento) ed il tracking (inseguimento), è necessario disporre di un ambiente di realtà virtuale. Questi nascono come sistemi di simulazione 3D allo scopo di osservare l'interazione di complessi modelli dinamici con l'ambiente circostante. Si pongono dunque come ultimo strumento di analisi, a valle delle simulazione ottenute in ambienti di calcolo numerico come Simulink (in modo del tutto equivalente utilizzando script Matlab), prima delle prove che saranno condotte sul sistema fisico. In gergo tecnico questo tipo di verifica è nota con l'acronimo SIL (Software-in-the-loop).
Questa è solo una delle tante applicazioni sviluppate negli ultimi anni, si prenda ad esempio quanto descritto in questo articolo.
In pratica, secondo tale metodologia SIL, il software di controllo da verificare viene fatto interagire direttamente con l'emulazione del sistema, a cui è destinato, per poterlo sollecitare come se fosse in condizioni operative. In questo modo è possibile effettuare una prima verifica, alienandosi in parte da quelli che saranno i prototipi fisici.
Il vantaggio di questo approccio è dato dalla possibilità di disporre di ambienti virtuali per il test utilizzando hardware standard (ad esempio un PC), evitando il ricorso a costosi sistemi di simulazione fisici come i banchi necessari per l'HIL (Hardware-in-the-loop) o a prototipi funzionanti.
La libreria per la virtualizzazione, inoltre, consente l'esportazione di frames (fotogrammi) durante le simulazioni, impiegabili come input, ad esempio, per processi di image processing per chiudere possibili loop di controllo.
Nel seguito descriveremo il sintetizzatore di scenari in Matlab, passando attraverso un esempio già strutturato di possibile impiego, vedremo come modificarli (sostituzione modello 3D, aggiunta di osservatori esterni, raccolta dei dati provenienti dai sensori virtuali, etc.), le alternative open e closed source presenti in letteratura, i sistemi di riferimento ed un breve accenno ai formalismi matematici necessari per descrivere il comportamento di un multi-rotore in un ambiente di realtà virtuale.
Infine, analizzeremo cos'è un sistema di riconoscimento e la loro importanza nei droni, riprendendo il concetto di visual servoing (asservimento visivo, discusso nel primo appuntamento). Introdurremo l'idea di visione artificiale ed object detection, i principali algoritmi basati sulle features, le problematiche relative al riconoscimento e quelle derivanti dall'architettura, concludendo con i problemi di alto e basso livello illustrandone le possibili soluzioni.
L'ambiente di realtà virtuale in Matlab
Al fine di ottimizzare i tempi di sviluppo, sfruttando un oggetto già realizzato a cui è stato conferita una specifica dinamica, è possibile utilizzare uno dei tanti esempi già strutturati, piuttosto che costruirne uno ex novo, utilizzando l'apposito editor.
In passato ci siamo già occupati di questa tipologia di applicazione, si veda, ad esempio, quanto descritto in un nostro articolo.
In quest'ottica, nell'ambito del corso, si è scelto di impiegare uno dei tanti esempi che coinvolgono la dinamica dei veicoli, in particolar modo quello sulla Skoda Octavia [L'esempio preso in considerazione è vr_octavia_2cars nel quale vengono simulati sia i movimenti longitudinali che quelli laterali del veicolo]: l'auto percorre (Figura 1) un tracciato relativamente complesso, lungo il quale è possibile osservare le forze che agiscono sui pneumatici e sulla carrozzeria, l'attivazione del sistema di frenata, il funzionamento della ECU (Engine Control Unit), etc. Tale scenario costituisce un esempio calzante dei benefici che si ottengono nella visualizzazione del complesso sistema dinamico nell'ambiente di realtà virtuale.
Allo scenario opportunamente modificato, agendo sul modello 3D (.wrl), si è aggiunto un osservatore esterno (il drone) che è in grado di muoversi in piena libertà (x, y, z, yaw, pitch e roll) all'interno dell'ambiente, osservando l'auto lungo il percorso, simulando così l'intero processo: dalla cattura delle immagini attraverso la camera on-board, alla loro elaborazione - analizzato nel seguito -, sino all'attuazione della legge di controllo - obiettivo finale del corso - che determina la nuova posa (posizione ed orientamento) dell'APR in modo che l'oggetto rimanga nel suo campo visivo.
In Figura 2 è riportato lo schema che riassume il funzionamento del sistema nel suo complesso.
Descrizione dello scenario
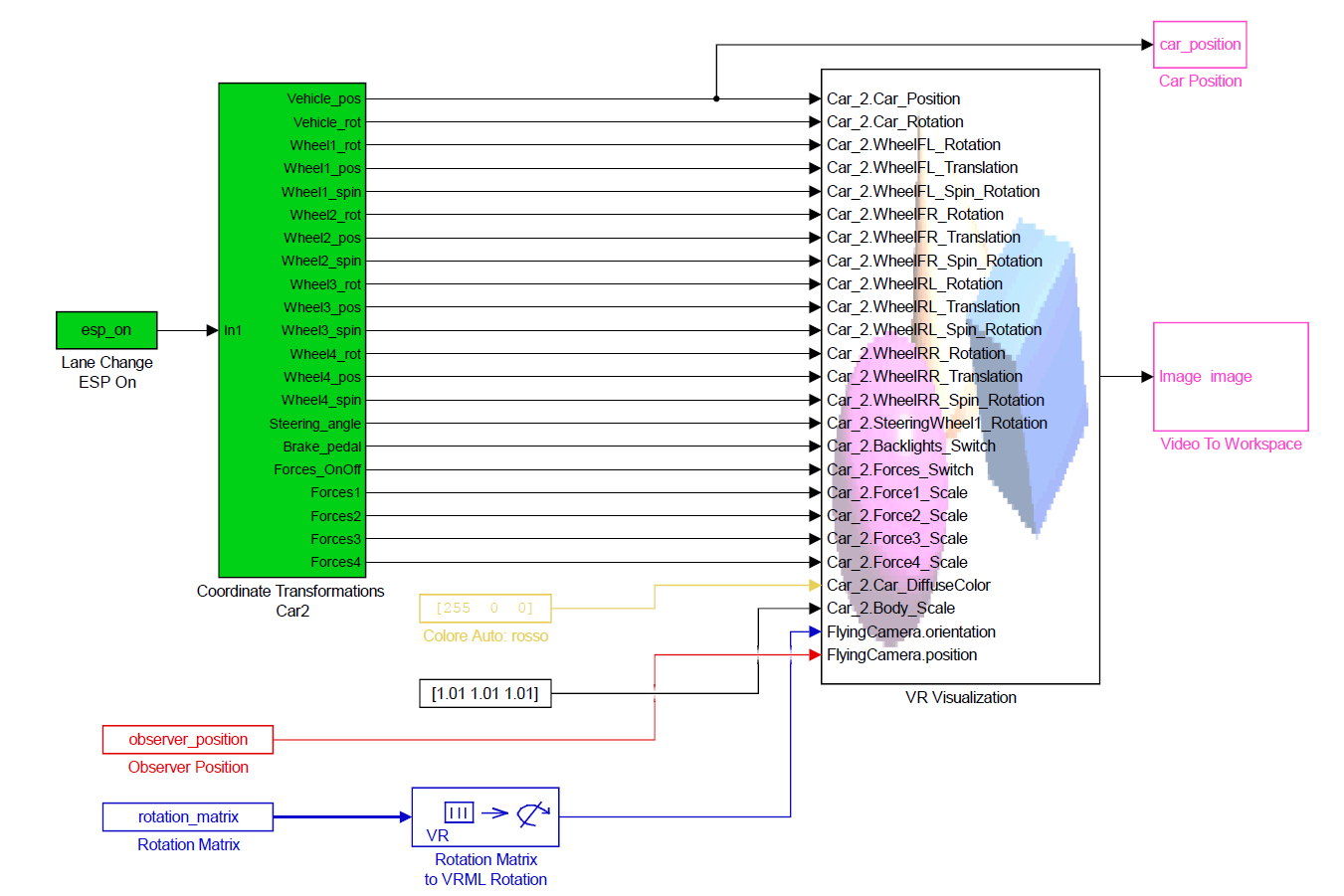
Lo scopo di questo paragrafo è descrivere lo schema Simulink (Figura 3) attraverso il quale è stato simulato lo scenario virtuale. Ogni sua parte è analizzata nel dettaglio per meglio comprendere i meccanismi che ne regolano il funzionamento.
La prima parte (in verde) si occupa di simulare la dinamica del veicolo sulla base delle informazioni contenute all'interno della serie temporale esp_on. Ad ogni frame, per tutta la durata della simulazione (pari a 33 secondi), viene calcolato l'angolo di sterzata, l'intensità della frenata, la velocità e la posizione dell'auto, le accelerazioni longitudinali e laterali, la forza che agisce su ogni pneumatico e sul corpo della vettura, etc. I risultati dell'elaborazione vengono poi trasferiti al blocco VR Visualization che farà muovere la macchina all'interno dello scenario.
Al contrario, la variabile observer_position (in rosso) indica la posizione dell'aeromobile (x, y, e z) fornita dal sistema di controllo; mentre rotation_matrix (in blu) ingloba al suo interno la matrice di rotazione globale (eq. 1) che, attraverso la formula di Rodrigues (eq. 2), consente di ricavare il quaternione (trattato nel seguito) necessario ad individuare l'orientamento del velivolo.
Entrambe le variabili sono ridefinite ad ogni passo durante la simulazione tenendo conto delle differenze che intercorrono tra il sistema di riferimento inerziale e quello virtuale (Figura 4), per poi essere trasmesse anch'esse al blocco VR Visualization.

Figura 4: La figura illustra il sistema di riferimento inerziale OFI (a sinistra) e quello virtuale OFVR (a destra).
I versi di crescenza degli angoli di Eulero (yaw, pitch e roll, chiariti nel paragrafo successivo), che definisco nello spazio l'orientamento del velivolo, seguono la regola della mano destra. Tale informazione è di estrema importanza perché determina i guadagni del regolatore (il sistema di controllo che varia la posa del velivolo di modo da non perdere di vista l'auto. Argomento dell'ultima lezione del mini corso). Inoltre, è bene precisare che l'auto, nella sua posizione iniziale, ha baricentro coincidente con il centro del sistema di riferimento inerziale.
Lo schema infine, ad ogni rendering, salva nel workspace di Matlab (in magenta) la posizione dell'auto ed un fotogramma dello scenario osservato dal punto di vista dellaeromobile, che sarà poi elaborato dall'algoritmo di detection (anch'esso illustrato nel seguito).
Il passo di integrazione, conseguentemente il numero di frames acquisiti dallo scenario durante la simulazione, è fisso ed è settato nella fase di inizializzazione.
Generatori di scenari: le alternative in letteratura
Nella robotica - contesto più ampio ma di cui fa parte questo lavoro - l'importanza degli ambienti di simulazione è in costante aumento. Rispetto al mondo reale, la simulazione fornisce molti vantaggi: nessuna limitazione nel numero di dispositivi, assenza di imprecisione in sensori ed attuatori, possibilità di debug e nessun rischio di danneggiare il robot reale (cosa assolutamente da non sottovalutare), e così via.
L'obiettivo di questo paragrafo è presentare i due ambienti più diffusi in letteratura: Gazebo e V-REP. Entrambi sfruttano le potenzialità messe a disposizione da ROS (Real-time Operating System): un sistema operativo real-time completo per lo sviluppo di applicazioni per robot e di alcuni software per l'interfacciamento con l'hardware.
V-REP
V-REP (Virtual Robot Experimentation Platform) è un simulatore sviluppato dalla Coppelia Robotics con lo scopo di simulare sistemi d'automazione industriale.
Nato nell'Agosto del 2012, è disponibile in quattro licenze: Player (gratuito), Pro Edu (gratuito per l'istruzione), Eval Pro (gratuito per usi non commerciali) e Pro (per uso commerciale); è noto come simulatore ibrido in quanto combina cinematica e dinamica con il fine di ottenere le migliori prestazioni negli scenari simulati.
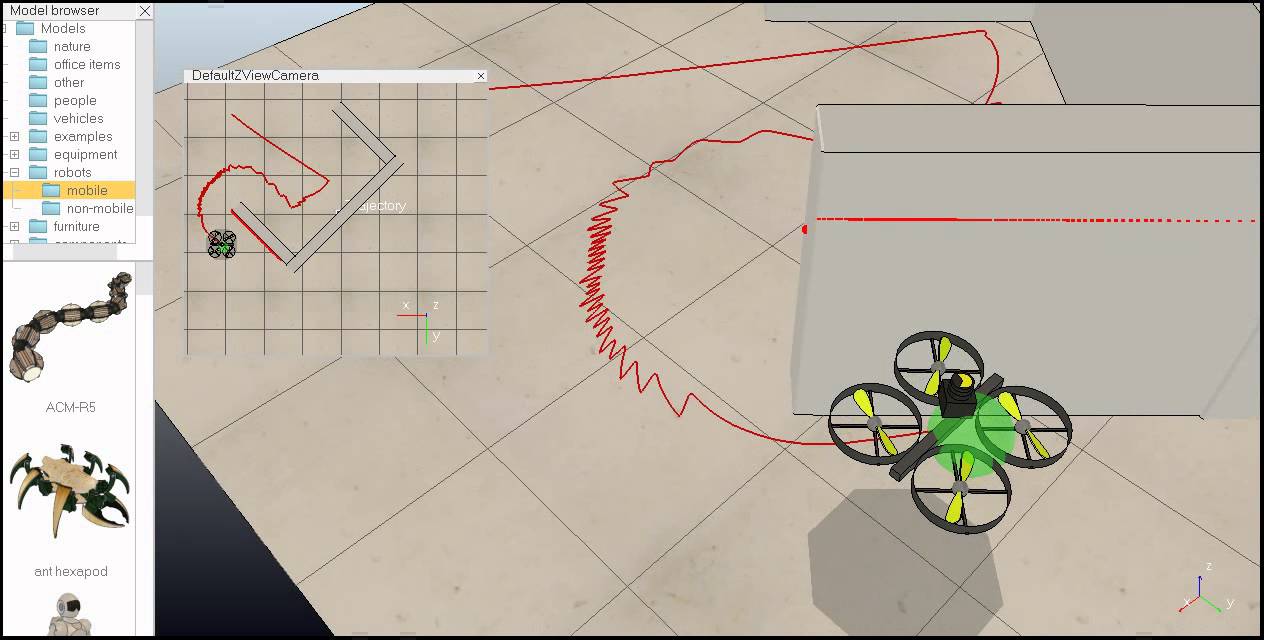
L'ambiente di sviluppo integrato (Figura 5) è basato su di un sistema di controllo distribuito: ciascun modello può essere controllato attraverso uno script incorporato, un plugin, un nodo ROS o un'API chiama da un client remoto. I controllori possono essere implementati in C/C++, Python, Matlab - da qui la possibilità di utilizzare il simulatore in modo del tutto equivalente all'ambiente proposto -, Lua ed Urbi. La disponibilità per sistemi operativi Windows, Linux e MacOS completa il quadro già ricco di per sé. Nel caso poi si sfrutti l'integrazione con ROS il trasferimento del controllo da un robot simulato ad un robot reale è immediato.
La documentazione è molto buona, copre tutti gli aspetti del simulatore, per di più la presenza di un forum consente agli utenti di porre le proprie domande, segnalare eventuali bug e richiedere nuove funzionalità, in pieno accordo al paradigma dell'open innovation. Infine, il simulatore è dotato di molteplici modelli pronti all'uso: persone, robot, umanoidi, robot industriali, facilitando così il compito dello sviluppatore che non deve ogni volta reinventare la ruota; dispone di molte funzionalità avanzate, come il rilevamento delle collisioni e la misura delle distanze minimi fra oggetti in tempo reale.
Gazebo
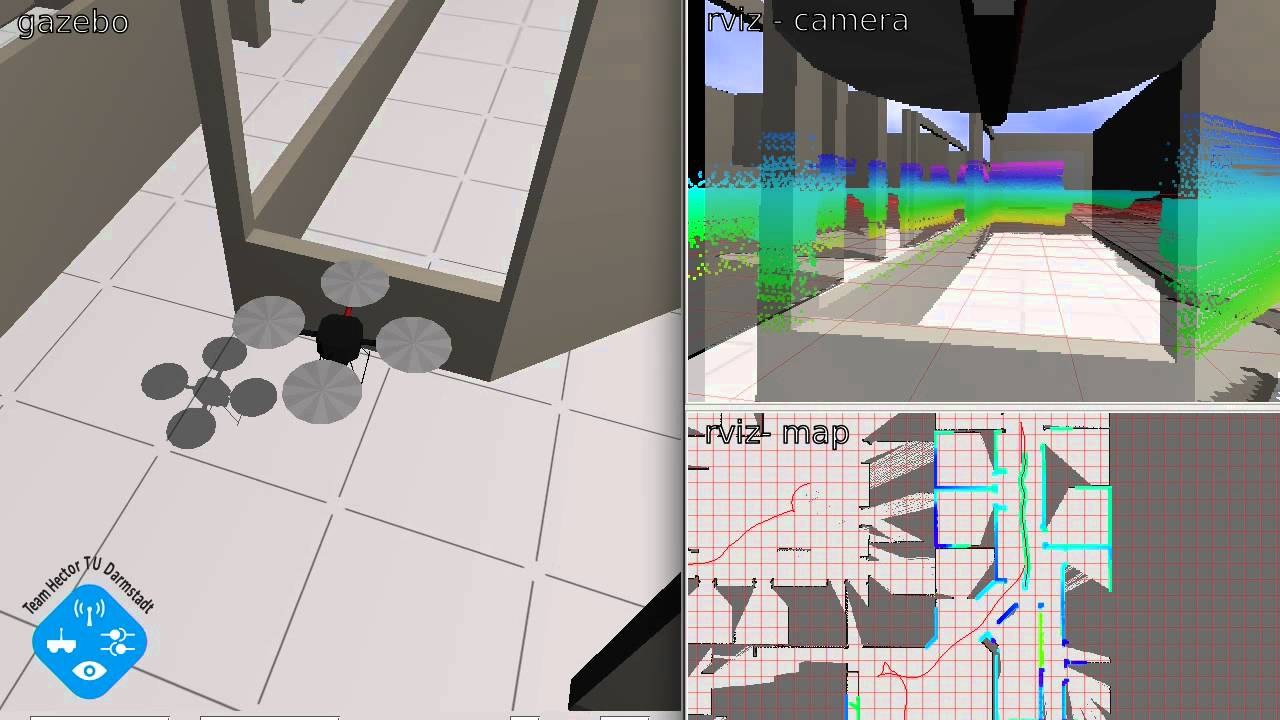
Gazebo (Figura 6) è un simulatore 3D open source che ha la capacità di simulatore gruppi di robot, sensori ed oggetti vari. Il progetto nato nel 2002 presso la University of Sourthern California, si pone l'intento di aiutare i ricercatori che lavorano con veicoli robotici in ambienti esterni (outdoor) ma è in grado anche di gestire ambienti interni (indoor).
Il simulatore è in grado di gestire vari tipi di oggetti, da semplici forme come cubi o sfere a modelli complessi come edifici o animali. Ogni soggetto ha le proprie caratteristiche: massa, velocità, frizione, proprietà fisiche che rendono la simulazione quanto più simile alla realtà. Inoltre, è disponibile un database di robot gestito dalla comunity, al quale tutti possono accedere, ed utilizzare per gli scopi più vari.
La documentazione di buon livello e la presenza di diversi tutorial, infine, aiuta chi si avvicina per la prima volta al simulatore. L'utilizzo dello strumento Gazebo Answer (in modo del tutto equivalente a quanto avviene per V-REP) consente agli utenti di pubblicare le proprie domande relative ai problemi o dubbi sull'utilizzo del simulatore. Grazie all'aiuto dei membri più esperti della comunità, e degli sviluppatori stessi di Gazebo, le domande vengono risposte in tempi brevi ed in modo adeguato permettendo ai nuovi utenti di migliorare le proprie capacità e conoscenze.
Sistemi di riferimento
Al fine di esprimere lo stato di un velivolo, e le relative equazioni dinamiche, è necessario definire un sistema di riferimento. Diversi sono quelli impiegati nell'ambito della meccanica del volo, e per la descrizione delle equazioni che ne modellano la dinamica:
- inerziale o ECI (Earth-centred inertial): con origine geocentrica, è orientato rispetto alle stesse fisse. L'asse Zi, coincidente con quello di rotazione terrestre, passa per il polo nord geografico; l'asse Xi è orientato secondo la direzione dell'equinozio di primavera e l'asse Yi, invece, è orientato in modo da rendere la terna levogira (o sinistrosa): terna di vettori di uno spazio affine applicati in uno stesso punto di origine O linearmente indipendenti, cioè non complanari;
- terrestre o ECEF (Earth-centered Earth-fixed): l'origine e l'asse Ze sono coincidenti, come nel sistema precedente, mentre l'asse Xe passa per il meridiano di Greenwich e l'asse Ye è tale da rendere la terna levogira. Assumendo trascurabile il modo di rivoluzione terrestre, questo sistema di assi non risulta inerziale solo a causa del moto di rotazione. Sebbene la terna ECEF non sia parziale, per i velivoli privi di pilota esistono le condizioni affinché sia considerata tale. Infatti, nell'ipotesi tempi di funzionamento molto brevi, il moto di rotazione può considerarsi trascurabile.
- verticale-locale o NED (North-East-Down): è assunto con l'origine fissata al baricentro del velivolo e l'asse Zv orientato verso il basso secondo la direzione della verticale locale. Gli assi Xv e Yv sono tali da individuare un piano normale alla Zv, con Xv orientato verso il Nord geografico, e Yv orientato verso Est in modo da rendere la terna levogira. Segue il velivolo nel moto intorno alla Terra, mantenendo invariato il suo orientamento;
- assi corpo con origine nel baricentro del velivolo, l'asse Xb coincidente con il suo asse longitudinale e diretto secondo la direzione di volo, l'asse Zb è contenuto nel suo piano di simmetria longitudinale e diretto verso il basso nelle condizioni di volo orizzontale, mentre l'asse Yb è tale da rendere la terna levogira;
- assi vento con origine nel baricentro, definisce l'asse Xw coincidente con direzione e verso della velocità relativa, che comprende l'eventuale contributo del vento, e l'asse Zw ortogonale e giacente nel piano di simmetria (Xb, Yb) del velivolo;
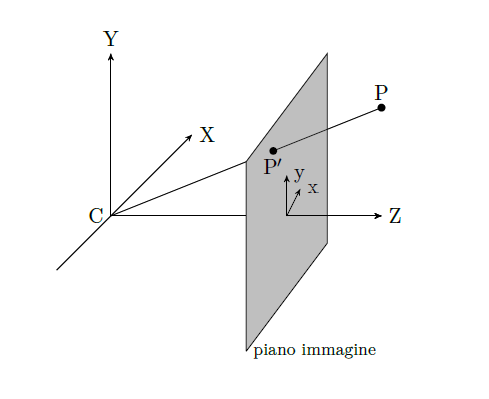
- assi camera (Figura 7) ha le stesse caratteristiche del sistema assi corpo necessario a descrivere in modo corretto il problema del riconoscimento ed inseguimento obiettivi. Esso è centrato nel baricentro della telecamera (per semplicità si suppone che il baricentro della telecamera e quello del velivolo coincidano).
Angoli di Eulero
Date due generiche terne di riferimento ortogonali, orientate nello spazio in modo qualsiasi, è sempre possibile allineare una terna con l'altra attraverso rotazioni successive.
Esistono diverse sequenze di rotazioni con cui è possibile ottenere l'allineamento delle terne, e specificando una di essere si descrive l'orientamento di una terna rispetto all'altra. In particolare, quando si considerano gli assi verticali-locali e gli assi corpo, si usa descrivere l'orientamento della seconda rispetto alla prima mediante la sequenza di angoli di Eulero: φ (roll), θ (pitch) e ψ (yaw). In questo modo è possibile descrivere l'assetto di un velivolo indicando il suo orientamento rispetto agli assi verticali-locali.
Gli angoli di Eulero rappresentano tre rotazioni successive da eseguire intorno agli assi di una terna inizialmente allineata con gli assi verticali-locali per allinearla agli assi corpo. La prima rotazione avviene intorno all'asse Zv di un angolo pari a ψ (l'angolo di imbardata, yaw angle), ottenendo una terna T', il cui asse X' è allineato con la proiezioni dell'asse Xb sul piano orizzontale individuato dagli assi Xv Yv. La successiva rotazione avviene intorno all'asse Y' di un angolo pari a θ (l'angolo di beccheggio, pitch angle), ottenendo una terna T'', il cui asse X'' risulta definitivamente allineato con l'asse Xb. L'ultima rotazione avviene intorno all'asse X'' di un angolo pari a φ (angolo di rollio, roll angle) che allinea completamente le due terne.
La rotazione globale, rispetto ad una terna fissa di riferimento, è caratterizzata dalla matrice Cb/r (matrice dei coseni direttori) che denota la trasformazione completa dal sistema di riferimento, nel nostro caso verticale-locale, al sistema assi-corpo. Abbreviando la scrittura delle funzioni seno e coseno rispettivamente con s e c, si ottiene:
Una valida alternativa agli angoli di Eulero nella descrizione dell'assetto del velivolo nei sistemi di calcolo, per l'assenza di punti di singolarità e vantaggi da un punto di vista computazionale, è fornita dai quaternioni. Quadruple di numeri reali considerati in un preciso ordine, possono essere rappresentati come un numero complesso generalizzato a quattro componenti:
con i2=j2=k2=ijk=-1, ij=k, jk=i, ki=j=-ik e costituiscono un tentativo di generalizzare i numeri complessi nel piano a tre dimensioni. Maggiori dettagli e proprietà al riguardo si rimandano al lettore più curioso.
Utilizzando la formula di Rodrigues è possibile rappresentare la matrice di rotazione globale Cb/r (eq. 1) in termini di una rotazione asse-angolo, dove r=(r1, r2, r3) esprime gli assi e θ l'angolo.
Visione artificiale
Il corrispettivo informatico della visione naturale è chiamato visione artificiale e rappresenta il meccanismo tramite il quale una macchina ottiene la possibilità di "vedere". Tramite le immagini digitali, anche un computer può sfruttare dei meccanismi simili alla vista: qualunque macchina, per poter elaborare un insieme di dati, ha bisogno che essi siano riportati ad un valore numerico, a dei bit. Grazie a modelli di colore, ad esempio il modello RGB (Red Green Blue), ogni immagine può essere rappresentata come una combinazione di termini numerici; nel modello RGB, tali valori indicano quanto ogni componente di rosso, verde e blu è presente in un determinato punto dell'immagine (il pixel).
La Figura 8 mostra la proprietà di additività del modello RGB. Combinando i tre colori di partenza è possibile crearne di nuovi, a loro volta, riutilizzabili allo stesso scopo. In ogni miscelazione, i colori possono essere pesati diversamente dando così più risalto ad un termine piuttosto che ad un altro, mentre la loro somma (se egualmente pesati) porta ad ottenere il bianco (per dualità, l'assenza di tutti i termini porta al nero). Un'immagine digitale, quindi, se gestita in questo modo, è facilmente rappresentabile come somma pesata dei tre livelli di colore. La Figura 9 mostra come la semplice immagine di un fiore è in realtà il frutto della proprietà di additività applicata a tre immagini, ognuna relativa ad un livello del modello RGB.
Il campo della visione artificiale (o computer vision) è ampio, tanti sono gli studi in corso d'opera. Sono, infatti, numerose le problematiche da affrontare. Le principali difficoltà riguardano la variabilità dei colori e la luminosità nella scena, gli oggetti complessi difficili da elaborare, e quelli solo parzialmente visibili (occultati da altre figure).
La possibilità di immettere conoscenza in un sistema artificiale attraverso procedimenti che riproducono i meccanismi sensoriali umani è noto come problema della percezione, ed è di primaria importanza nella costruzione di sistemi intelligenti. Alcune di queste difficoltà (in particolare quelle relative all'illuminazione) sono generalmente attenuate in ambienti chiusi (indoor), ancora di più quando le fonti di luce sono artificiali, ed è per questo motivo che molti studi ed esperimenti di computer vision vengono effettuati in uffici o laboratori.
Il meccanismo che regola il funzionamento della visione artificiale è abbastanza semplice: attraverso l'ausilio di una videocamera si scatta una foto dell'ambiente (sia esso reale o virtuale), l'immagine viene poi convertita in una matrice di pixel, nient'altro che una griglia bidimensionale di valori abbastanza grande da coprire le dimensioni dell'intero fotogramma. Supponendo che l'immagine sia a colori, vengono formate tre matrici (una per ogni colore primario additivo) ed ognuno dei loro elementi assume un valore pari alla quantità del rispettivo colore in quel determinato punto dell'immagine. Generalmente questi valori sono compresi tra 0 (assenza di colore) e 255 (massimo valore di colore possibile). Una volta digitalizzata l'immagine, si può procedere con l'elaborazione per estrarre le informazioni sulla scena.
[...]
ATTENZIONE: quello che hai appena letto è solo un estratto, l'Articolo Tecnico completo è composto da ben 7272 parole ed è riservato agli ABBONATI. Con l'Abbonamento avrai anche accesso a tutti gli altri Articoli Tecnici che potrai leggere in formato PDF per un anno. ABBONATI ORA, è semplice e sicuro.




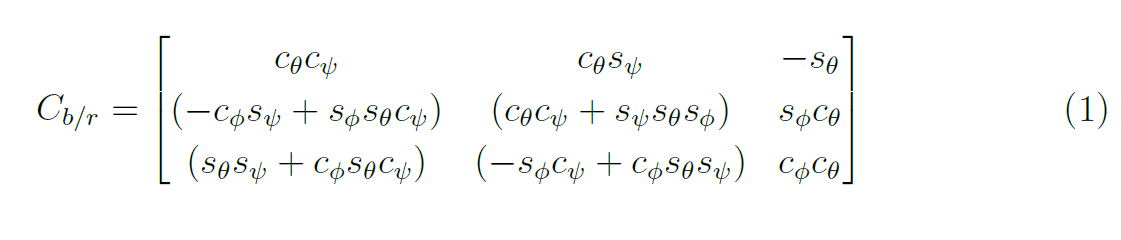
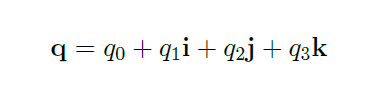
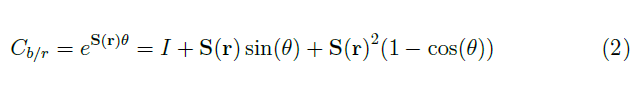







In questi casi Matlab si dimostra decisamente all’altezza per eseguire simulazioni e modelli volti a definire un corretto sistema.
Articolo molto interessante, gli argomenti trattati sono stati davvero tanti. Personalmente mi interesserebbe approfondire la parte di simulazione, in particolare l’interazione tra il modello e lo scenario. Sai se è possibile utilizzare qualche editor di scenario (magari free) per rappresentare ad esempio le strade di una particolare città o area geografica? Ben approfondito anche l’argomento dei sistemi di riferimento, in particolare la trasformazione tra coordinate body (corpo nell’articolo) e navigation (inerziale) e viceversa, una chiara applicazione del calcolo matriciale, molto utilizzata in avionica.
Come tool open-source ti consiglio Blender, anche se non è conosciuto per l’essere tra i più semplici. Tieni sempre a mente che MATLAB è un software commerciale dunque difficilmente troverai qualche editor tanto utile quanto quello che mette a disposizione la piattaforma. Strumento, invece, più potente ma anche più complesso è GAZEBO che ha tra le sue l’essere open-source.
Secondo me Matlab è il migliore, non so se software simili tipo Octave fanno le stesse cose…