
Il Raspberry Pi 3 dispone di un processore decisamente più veloce e potente dei precedenti modelli. Per il suo basso consumo e per le prestazioni della sua CPU si può iniziare a pensare ad utilizzarlo anche per la ricerca matematica. L'articolo che segue tratta della creazione di un software per la ricerca di numeri primi estremamente grandi (composti anche da migliaia di cifre).
I numeri primi
La particolarità risiede nel fatto che quando un numero primo viene trovato, si illumina una lampada di potenza ad esso collegata e viene emesso anche un avviso acustico. Il perché? Tra i matematici, la scoperta di numeri primi molto grandi, costituisce sempre un evento molto importante e gioioso.
Si studiano già dalle scuole elementari e medie. Si tratta di valori che si possono solo dividere per 1 e per se stessi. Trovare un numero primo piccolo "n" è molto semplice, è sufficiente "scandagliare" tutti i divisori compresi tra n+1 e sqrt(n) per trovare, eventualmente, un suo divisore. Occorrerebbero miliardi di anni per la sua determinazione. Lo stesso criterio non può essere, ovviamente, adottato per la ricerca di numeri primi composti da decine di migliaia di cifre. Tra i matematici, come detto nell'introduzione, esiste una sorta di sfida per chi riesce a scovare il numero primo più grande possibile. Essi sono molto rari, come delle pietre preziose, man mano che si fanno più grandi. Non esiste ancora una formula matematica per la loro determinazione e il problema di tali numeri è uno dei più importanti casi irrisolti della matematica e della teoria dei numeri. Nella pratica essi sono utilizzati nella crittografia dei dati. Alla data del presente articolo la classifica dei top-10 numeri primi è la seguente:
| # | Numero primo | Cifre | Anno scoperta |
| 1 | 274.207.281-1 | 22.338.618 | 2016 |
| 2 | 257.885.161-1 | 17.425.170 | 2013 |
| 3 | 243.112.609-1 | 12.978.189 | 2008 |
| 4 | 242.643.801-1 | 12.837.064 | 2009 |
| 5 | 237.156.667-1 | 11.185.272 | 2008 |
| 6 | 232.582.657-1 | 9.808.358 | 2006 |
| 7 | 10.223*231.172.165+1 | 9.383.761 | 2016 |
| 8 | 230.402.457-1 | 9.152.052 | 2005 |
| 9 | 225.964.951-1 | 7.816.230 | 2005 |
| 10 | 224.036.583-1 | 7.235.733 | 2004 |
Uno dei più importanti siti di ricerca è questo, gestito e mantenuto dal Professor Chris K. Caldwell. Anche io ero, anni fa, un attivo ricercatore (vedi figura 1), ma ho dovuto interrompere poiché i PC, accesi 24 ore al giorno, consumavano tanta corrente elettrica, con un costo in bolletta non proprio indifferente.
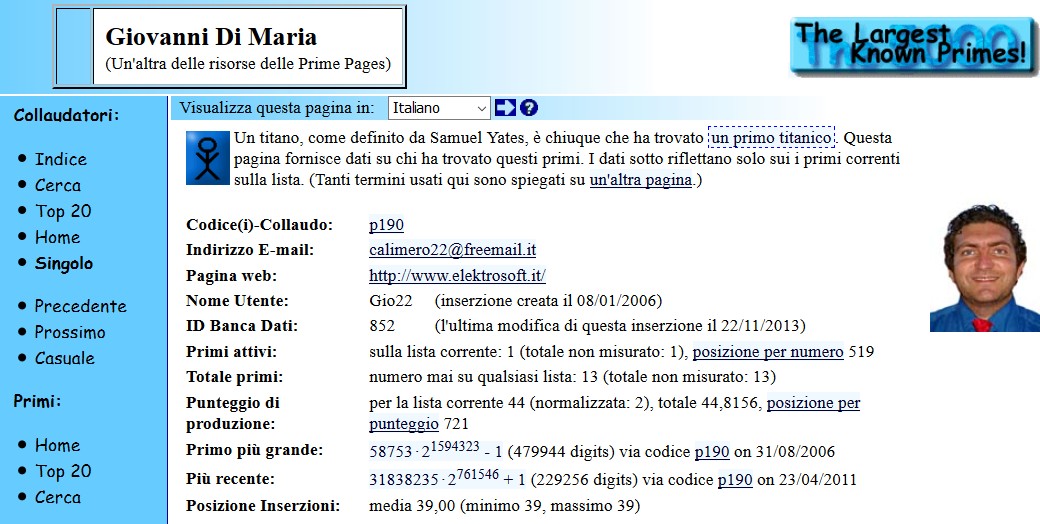
Figura 1: la ricerca di numeri primi.
Di seguito un mio numero primo molto grande, scoperto nel 2006 e composto da ben 479944 cifre (vedi figura 2). Al momento della sua determinazione esso occupava la posizione 39 della classifica mondiale, un risultato davvero notevole. Adesso, a distanza di undici anni, esso è "sceso" verso il 2000° posto, per via delle nuove scoperte con PC molto potenti. Può essere osservato a questo link. La sua formula canonica è la seguente:
58753* 21594323-1
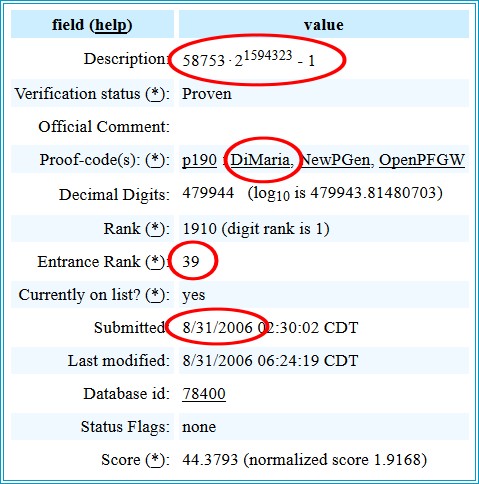
Figura 2: Il numero primo da me scoperto.
Raspberry Pi 3 e GMP
Come ci può aiutare il Raspberry Pi 3 a trovare numeri primi? Una delle possibili soluzioni è quella di scrivere un apposito programma, in linguaggio C con l'ausilio delle librerie matematiche GMP, esaminate in questo articolo. Il software dovrebbe chiedere all'utente di inserire, tramite tastiera, un grosso esponente. Da quel punto, la ricerca può iniziare, incrementando il numero di volta in volta.
La particolarità di tale software è anche quella di accendere una lampada collegata al Raspberry e di produrre un tono acustico in caso venga scoperto un numero primo. Abbiamo detto che si tratta di un evento molto importante, per i matematici, ed è giusto che tale evenienza sia festeggiata con le giuste attenzioni.
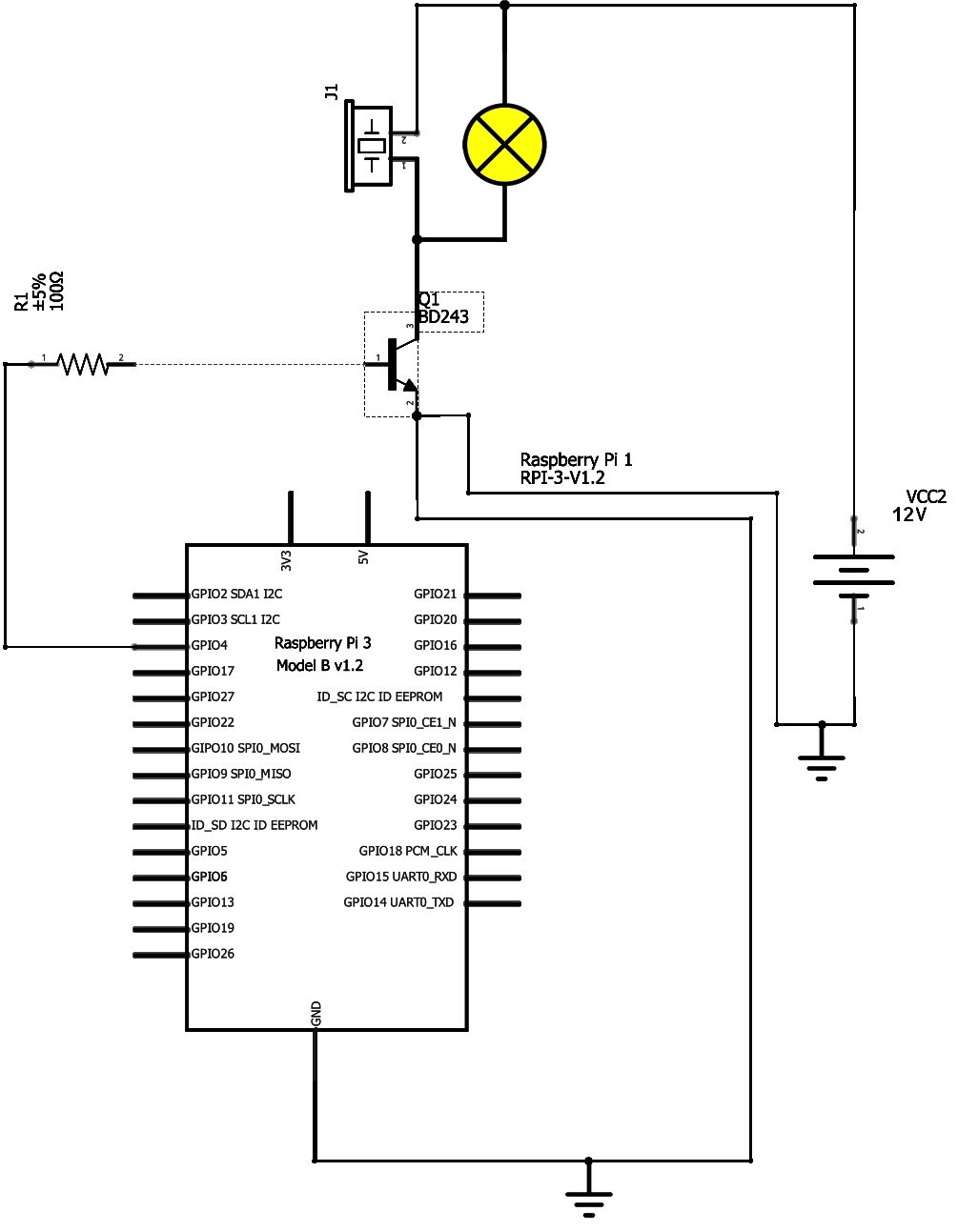
Schema elettrico
Lo schema elettrico risulta alquanto semplice ed è visibile in figura 3. La porta GPIO4, configurata come uscita dal software, pilota la base del transistor di potenza NPN BD243. Esso, quando si trova in stato di conduzione, riesce a fare scorrere una corrente sufficiente per illuminare la lampada di potenza ed attivare il buzzer. Entrambi i carichi funzionano a 12V.
Il cablaggio del circuito, invece, è raffigurato in figura 4.
Il codice
Per l'utilizzo delle librerie matematiche GMP occorre, ovviamente, averle installato preliminarmente. Si digiti con un editor il listato di cui sotto, in linguaggio C, e si proceda alla compilazione con il comando da console:
sudo gcc -Wall primi.c libgmp.a
Se tutto il lavoro è esente da errore il compilatore produce il file binario "a.out", che si manda in esecuzione con il comando:
sudo ./a.out
Commentiamo, adesso, le righe principali del programma.
- La porta GPIO4 del Raspberry Pi 3 è trattata come uscita, come spiegato nel nostro corso di cui a questo articolo;
- Il programma chiede, tramite tre funzioni "scanf", di inserire i valori di k, n, q;
- All'interno del ciclo infinito, il programma ricostruisce l'intero numero, la cui espansione potrebbe risultare alquanto elevata;
- Se il test di primalità, o di pseudoprimalità, è verificato, lo schermo avvisa con un opportuno messaggio e, contestualmente, si illumina la lampada di potenza e si ode una nota acustica sul buzzer;
- Il programma è a ciclo infinito e per interromperlo occorre premere la sequenza dei tasti CTRL-C.
Si ricorda che il programma esaminato cerca i numeri primi nella forma:
k*2n+q
con k, n, q arbitrari. La primalità è controllata grazie all'utilizzo della funzione "mpz_probab_prime", eseguendo 5 test probabilistici di Miller-Rabin. Aumentando tale parametro la verifica risulta più attendibile ma lenta.
#include <stdio.h>
#include "gmp.h"
int main()
{
mpz_t p;
unsigned long k,n,q;
int test;
int tasto;
FILE *handle;
/*------Crea porta GPIO4------*/
handle=fopen("/sys/class/gpio/export","w");
fprintf(handle,"4");
fclose(handle);
/*-----GPIO4 in uscita------*/
handle=fopen("/sys/class/gpio/gpio4/direction","w");
fprintf(handle,"out");
fclose(handle);
/*------Sèegne Lampada-----*/
handle=fopen("/sys/class/gpio/gpio4/value","w");
fprintf(handle,"0");
fclose(handle);
/*---------Messaggi e inserimento valori da tastiera-----*/
printf("\n\n\n\n\n\n\n\n\n\n");
printf("Questo programma cerca NUMERI PRIMI grandi\n");
printf("nella forma k*2^n+q \n\n");
printf("Inserire il valore di k: ");
scanf("%ld",&k);
printf("Inserire il valore di n: ");
scanf("%ld",&n);
printf("Inserire il valore di q: ");
scanf("%ld",&q);
/*-----------------Inizializza------------------*/
mpz_init(p);
/*------------Ricostruisce k*2^n+q-------------*/
q=q-1; /* Decrementa q per comodita'*/
while(1) {
q=q+1;
mpz_ui_pow_ui(p,2,n); /* Calcola 2^n */
mpz_mul_ui(p,p,k); /* Il risultato per k */
mpz_add_ui(p,p,q); /* Il risultato piu' q */
/*-------Inizia ricerca----------*/
printf("Testing %ld*2^%ld+%ld.......\n",k,n,q);
test=mpz_probab_prime_p(p,5);
/*----------Se p e' un probabile numero primo------*/
if(test>0) {
/*------Accende Lampada-----*/
handle=fopen("/sys/class/gpio/gpio4/value","w");
fprintf(handle,"1");
fclose(handle);
/*---------------------Messaggi a video-------*/
printf("=====================================================\n");
printf("ATTENZIONE: %ld*2^%ld+%ld e' probabilmente PRIMO \n",k,n,q);
printf("=====================================================\n");
printf("Digitare 0 e <INVIO> per continuare\n");
scanf("%d",&tasto);
/*------Sèegne Lampada-----*/
handle=fopen("/sys/class/gpio/gpio4/value","w");
fprintf(handle,"0");
fclose(handle);
}
}
return 0;
}
Esempio di utilizzo
Avviando il programma, come detto prima, l'operatore è invitato ad immettere i valori arbitrari di k, n, q, come mostrato in figura 5. Inizialmente non conviene esagerare nella grandezza dei numeri, specialmente per l'esponente "n". Si provi, ad esempio, inserendo i seguenti parametri:
- per k inserire 100;
- per n inserire 10000;
- per q inserire 1.
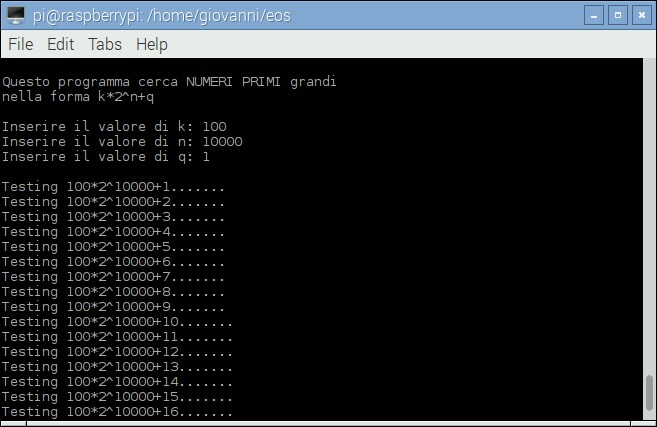
Figura 5: Utilizzo del programma.
Immediatamente il programma inizia a scandagliare, secondo le direttive imposte, i numeri candidati. Per alcuni valori, la ricerca sarà più lenta. Dopo alcuni minuti il programma, finalmente, trova un numero primo, come mostrato in figura 6, e la lampada e il buzzer vengono attivati. Per continuare la ricerca è sufficiente digitare un numero e premere invio. I carichi del transistor saranno immediatamente disattivati.
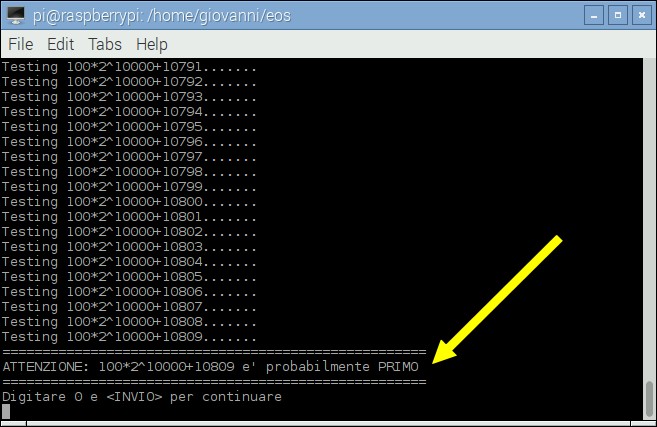
Figura 6: Il programma ha trovato un probabile numero primo.
L'espansione del numero 100*210000+10809 è la seguente, ben 3013 cifre e non si sa neppure leggerlo:
199506311688075838488374216268358508382349683 1886192454852008949852943883022194663191996168 40361945978993311294232091242715564913494137811 17593785932096323957855730046793794526765246551 2660598955205500869181933115425086084606181046 855090748660896248880904898948380092539416332 5785062156830947390255691238806522509664387444 10467598716269854532228685381616943157756296407 6283688076073222853509164147618395638145896946 3899410840960536267821064621427333394036525565 64953060314268023496940033593431665145929777327 96657756061725820314079941981796073782456837622 8003730288548725190083446458145465055792960141 48339216157345881392570953797691192778008269577 3567444412306201875783632550272832378927071037 38028663930314281332414016241956716905740614196 54342324638801248856147305207431992259611796250 1309928602417083408076059323201612684922884962 5584131284406153673895148711425631511108974551420 33138202029316409575964647560104058458415660720 449628670165150619206310041864222759086709005746 064178569519114560550682512504060075198422618980 592371180544447880729063952425483392219827074044 7316237676084661303377870603980341319713349365462 2700563169937455508241780972810983291314403571877 524768509857276937926433221599399876886660808368 8378380276432827751722736575727447841122943897338 1086160742325329197481312019760417828196569747589 816453125843413595986278413012818540628347664908 869052104758088261582396198577012240704433058307 586903931960460340497315658320867210591330090375 28234155397453943977152574552905102123109473216107 534748257407752739863482984983407569379556466386 21874569499279016572103701364433135817214311791398 222983845847334440270964182851005072927748364550 5786345011008529878123894739286995408343461588070 43959118985815145779177143619698728131459483783202 08147498217185801138907122825090582681743622057747 59214176537156877256149045829049924610286300815355 8330813010198767585623434353895540917562340084488 7526162643568648833519463720377293240094456246923 25435040067802727383775537640672689863624103749141 09667185570507590981002467898801782719259533812824 2195402830275940844895501467666838969799688624163 63133763939033734558014076367418777110553842257394 99110186468219696581651485130494222369947714763069 155468217682876200362777257723781365331611196811280 7926694818872012986436607685516398605346022978715 57517947385246369446923087894265948217008051120322 36549628816903573912136833839359175641873385051097 027161391543959099159815465441733631165693603112224 99379699992267817323580231118626445752991357581750 0819983923628461524988108896023224436217377161808 635701546848405862232979285387562348655644053696 2622018963571028812361567512543338303270029097668 650568557157505516727518899194129711337690149916181 31517154400772865057318955745092033018530484711381 831540732405331903846208403642176370391155063978 90007428536721962809034779745333204683687958685 8023795221862912008074281955131794815762444829851 846150970488802727472157468813159475040973211508 049819045580341682694978714131606321068639151168 177430479259670948409
Grande gioia si prova quando un numero primo particolarmente grande viene trovato. La figura 7 mostra la lampada accesa proprio in questa evenienza.

Figura 7: La segnalazione luminosa e sonora per la scoperta di un numero primo.
Dopo qualche ora di ricerca, il programma è riuscito a scovare i seguenti numeri primi:
| Numero primo | Cifre |
| 100*210000+10809 | 3013 |
| 100*210000+19203 | 3013 |
| 100*210000+22447 | 3013 |
| 100*210000+28387 | 3013 |
| 100*210000+29091 | 3013 |
Conclusioni
Al di là dell'esempio concreto trattato, l'articolo ha voluto mettere in evidenza la possibilità di interfacciare qualunque tipologia di periferica esterna al Raspberry, con un proprio programma personalizzato, in modo da poter attivare un qualsiasi carico quando certe condizioni lo impongono. Buona sperimentazione a tutti.






Ci sono alcuni istituti di ricerca che per moltiplicare la potenza dei Raspberry hanno ben pensato di collegarne tanti tra loro in matrici. Quello che si ottiene è un computer estremamente potente, economico e dal consumo relativamente basso.
Collegare tanti Raspberry di sicuro aumenta le performance ma bisogna valutare i consumi in confronto con altre soluzioni. Ormai il Raspberry trova spazio in molte soluzioni, a cominciare dai sistemi DAQ/controllo negli esperimenti scientifici, passando per varie applicazioni industriali. Negli esperimenti più complessi, gli istituti di ricerca preferiscono però utilizzare altre soluzioni sia per una questione di esperienza già acquisita, ma anche perchè la mole di dati è notevole così come l’elaborazione e l’analisi.
Un esempio di utilizzo di una moltitudine Rapsberry Pi è stato quello di aumentare la potenza di calcolo al fine del guadagno di bitcoin. Ad oggi però penso quella strada non sia più percorribile….