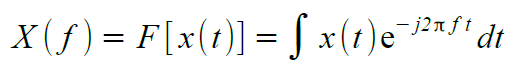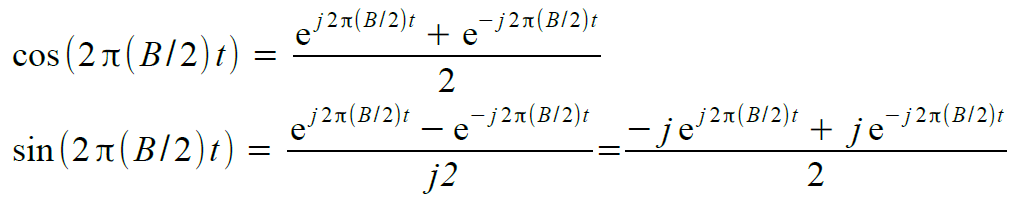Un sistema basato su Software-Defined Radio (SDR) è un sistema di comunicazione radio che utilizza un software per la modulazione e la demodulazione dei segnali radio. Utilizzare una SDR vuol dire implementare via software ciò che prima era fatto in hardware, con una serie notevole di vantaggi. In questo articolo, andremo a descrivere la progettazione di uno schema di comunicazione SC-SSB con il Metodo di Weaver, implementato mediante il framework SDR GNU Radio.
Introduzione
Il framework GNU Radio è stato introdotto e descritto in precedenti articoli pubblicati sul sito web di Elettronica Open Source. In questo articolo, invece, ci focalizzeremo su cosa sia il Metodo Weaver e su come implementarlo mediante il framework SDR.
Storicamente, la modulazione AM è stato il primo metodo di comunicazione radiofonica per voce/musica, e anche se facile da implementare in hardware, presenta una serie di svantaggi rispetto ad altre modulazioni. In particolare, per comunicazioni ad alta frequenza:
- La maggior parte della potenza del segnale trasmesso è contenuta all'interno della portante (che è trasmessa continuamente, anche in assenza di segnale audio), rendendo AM energeticamente molto inefficiente.
- La larghezza spettrale della forma d'onda AM è il doppio della larghezza di banda audio, ed è quindi un uso inefficace dello spettro radio ad alta frequenza.
- Nella comunicazione a lunga distanza può verificarsi perdita di intelligibilità del segnale.
La modulazione con portante soppressa e banda laterale singola (SC-SSB) è una variante della modulazione d'ampiezza (AM) ed è ampiamente utilizzata nelle comunicazioni radiofoniche ad alta frequenza, come quelle marittime, e nella comunicazione vocale radioamatoriale. L'introduzione di tale variante ha comportato l'eliminazione della portante e di una delle due bande laterali dalla trasmissione AM, lasciando solo la banda laterale superiore (USB) o inferiore (LSB). Si noti che in questo modo sono stati risolti i due punti critici della trasmissione AM, ovvero: non c'è più potenza trasmessa dalla portante e la potenza trasmessa in assenza di segnale è zero, la larghezza di banda è la metà di quella di un segnale AM.
I metodi per generare un segnale SSB sono generalmente due: il metodo del filtraggio e il metodo dello spostamento di fase. Il metodo dello spostamento di fase è probabilmente il più utilizzato, ma il suo principale svantaggio è che la rete di sfasamento deve essere in grado di realizzare uno sfasamento costante di π/2 radianti (90°) su tutta la larghezza di banda. Il design di tale rete può essere difficile da realizzare, e il verificarsi di errori nello sfasamento può portare a soppressione incompleta della banda laterale indesiderata.
Il Metodo Weaver (noto anche come Terzo Metodo) presenta numerosi vantaggi rispetto ai classici due, anche se può risultare più complesso da capire. Con l'avvento dei DSP (Digital Signal Processing) e degli SDR (Software Defined Radio) il metodo Weaver viene oggi sempre più utilizzato nelle comunicazioni radio mobili, anche se non è ancora generalmente ben compreso dagli hobbisti. Il metodo Weaver elimina la necessità della rete di sfasamento e la sostituisce con una coppia di filtri passa-basso identici e con specifiche di progettazione modeste.
Nozioni preliminari
Prima di parlare del topic dell'articolo, ci servono alcune nozioni di base di teoria dei segnali.
Se un segnale x(t) assume valori in funzione della variabile temporale t, allora il suo contenuto in frequenza X(f) è dato dalla trasformata di Fourier del segnale nel tempo come:
La trasformata di Fourier di una costante A risulta pari ad una delta di Dirac alla frequenza 0 Hz e con area integrale di valore A.
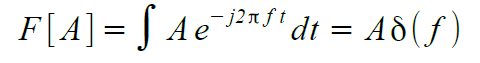Per analogia con la trasformata di una costante, allora la trasformata di un esponenziale complesso sarà una delta di Dirac alla frequenza f0.
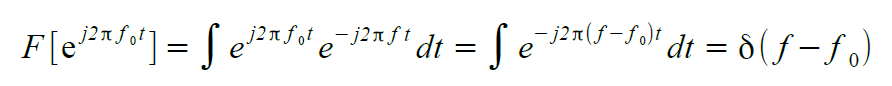Se un segnale x(t) viene moltiplicato per un esponenziale complesso a frequenza f0, allora la trasformata di Fourier di questo prodotto si traduce nella traslazione di X(f) dalla frequenza 0 Hz alla frequenza f0.
I segnali reali presentano una trasformata di Fourier simmetrica rispetto alla frequenza 0 Hz.
Nella modulazione a doppia banda laterale (DSB) di un segnale reale x(t), l'asse di simmetria dello spettro si sposta dalla frequenza 0 Hz alle frequenze -fc e +fc (dove fc è la frequenza della portante), e gli intervalli di frequenze ai lati di ogni asse sono chiamati bande laterali.
La modulazione a banda laterale singola (SSB) elimina una banda laterale di ciascun asse, pur preservando il segnale.
Architettura modulatore Weaver
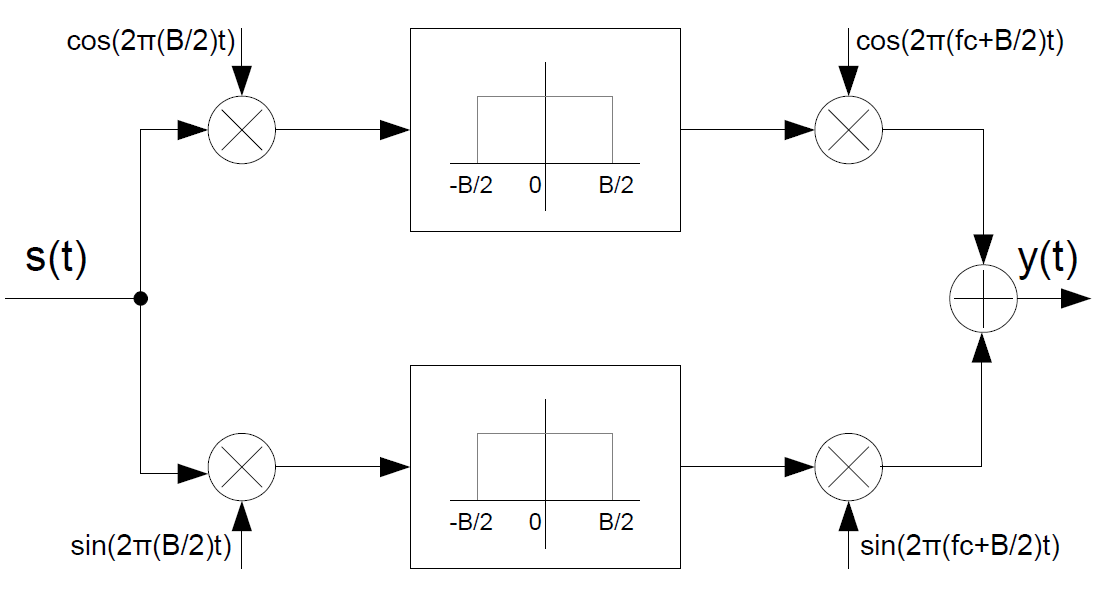
L'architettura del modulatore Weaver per generare un segnale SSB a portante soppressa viene riportata in Figura 1:
Figura 1: Schema a blocchi del modulatore Weaver
Dove s(t) rappresenta il segnale che trasporta il messaggio, y(t) l'uscita modulata, fc la frequenza della portante e B la banda monolatera di s(t).
Come si vede dalla Figura 1 il segnale s(t) viaggia su due cammini paralleli, necessari per la generazione dei segnali "in fase" e "in quadratura".
Nel cammino in alto (in fase), s(t) viene moltiplicato per il cos(2π(B/2)t) mentre nel cammino in basso (in quadratura) viene moltiplicato per il sin((2π(B/2)t). Dalle Formule di Eulero sappiamo che:
A causa delle prime due moltiplicazioni nel modulatore, il segnale s(t) subisce quindi due traslazioni su entrambi i cammini. Una copia viene traslata alla frequenza -B/2 e una alla frequenza B/2. Tutte le copie hanno ampiezza dimezzata rispetto allo spettro del segnale d'origine.
La Figura 2 illustra quello che avviene allo spettro del segnale s(t) dopo le moltiplicazioni sui due cammini:
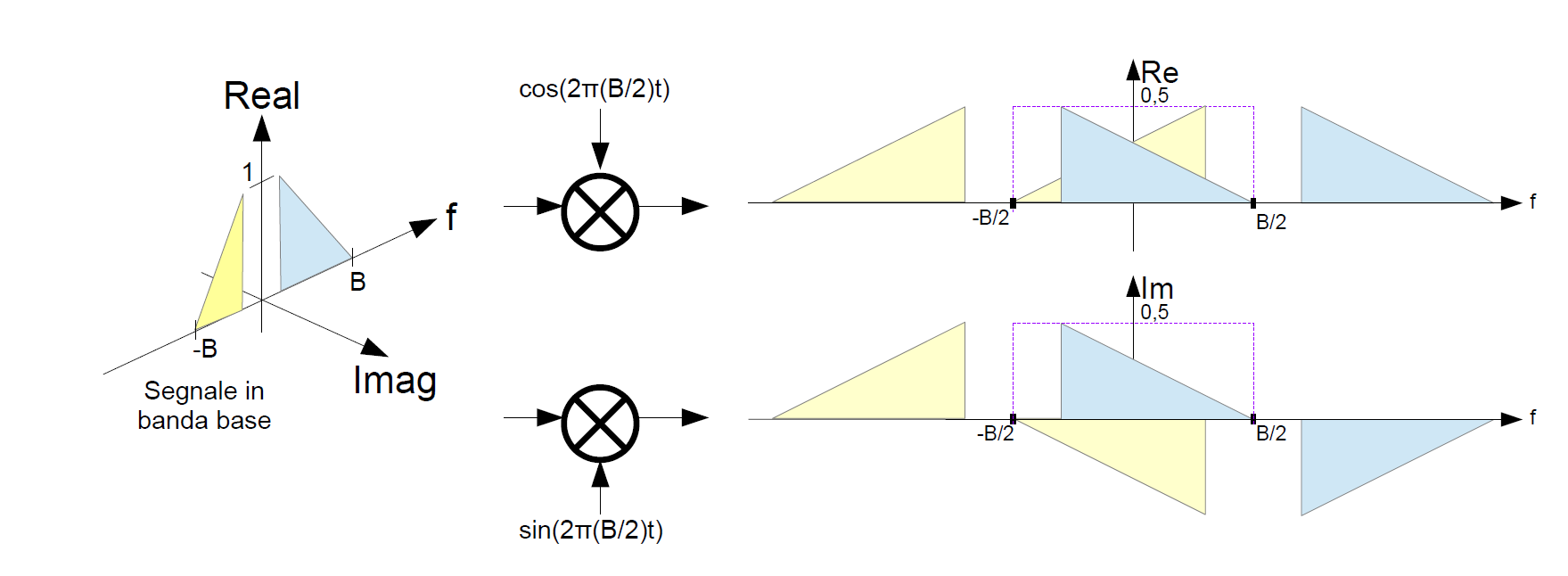
Figura 2: Lo spettro del segnale in banda base presenta solo componenti reali. Il prodotto con la funzione seno trasla le componenti sul piano immaginario. Il riquadro viola rappresenta le frequenze selezionate dal filtro passo basso presente dopo i primi due mixer
Lo spettro di un segnale presenta generalmente una componente reale ed una immaginaria, che abbiamo rappresentato in Figura 2 come due piani ortogonali tra loro.
Il nostro segnale essendo reale presenta uno spettro con una componente reale, simmetrica rispetto alla frequenza 0 Hz. Dopo la moltiplicazione con il coseno, lo spettro viene traslato nell'intorno delle frequenze +B/2 e -B/2. Mentre, dopo la moltiplicazione con il seno il segnale subisce la stessa traslazione ma nel piano immaginario a causa dell'unità immaginaria j che moltiplica gli esponenziali complessi (vedi Formule di Eulero). Inoltre, la replica traslata a +B/2 subisce un ribaltamento di fase a causa del segno meno (vedi Formule di Eulero).
Nella Figura 2 è presente un riquadro tratteggiato di colore viola, che rappresenta le frequenze selezionate dai filtri passa basso presenti all'uscita dei primi due mixer. Tali filtri servono a selezionare le componenti spettrali ubicate nell'intervallo che va da -B/2 a +B/2 e ad eliminare tutte le altre.
A questo punto, i due segnali in uscita dai filtri subiscono una seconda moltiplicazione come riportato in Figura 3.
ATTENZIONE: quello che hai appena letto è solo un estratto, l'Articolo Tecnico completo è composto da ben 2503 parole ed è riservato agli ABBONATI. Con l'Abbonamento avrai anche accesso a tutti gli altri Articoli Tecnici che potrai leggere in formato PDF per un anno. ABBONATI ORA, è semplice e sicuro.
