
Dopo aver visto la routine che esegue la crittografia secondo l’algoritmo Rolling Code nell’articolo "Routine di Encryption della codifica RollingCode", è giunto il momento di descrivere, nell’ultimo dei cinque articoli, la routine che esegue la decrittografia.
Il funzionamento di questa routine è molto simile a quello della routine di crittografia ma con delle differenti operazioni sui bit tali da realizzare l’algoritmo di decrittografia.
Anche questa routine di può essere rappresentata da uno schema che racchiude e rappresenta gli step che l’algoritmo deve eseguire la topologia della figura è differente da quella usata nell’articolo "Routine di Encryption della codifica RollingCode", ma comunque chiara ed utile al nostro scopo):
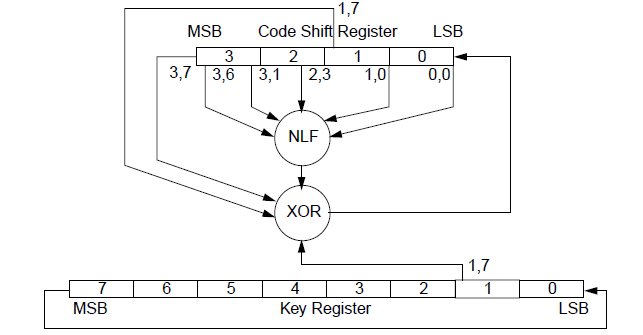
Anche per questo algoritmo, prima di passare alla spiegazione nel dettaglio, vediamo quali sono gli “attori” che entrano in gioco: partendo dall’alto in basso delle figura incontriamo una word a 32 bit che corrisponde al valore che dovrà essere decriptato; più in basso abbiamo la NLF (già citata nell’articolo "Routine di Encryption della codifica RollingCode"), ossia la “Non Linear Function”, la quale genera ad ogni ciclo un bit il cui valore dipende da cinque bit di ingresso opportunamente selezionati; sotto la NLF troviamo un’operazione di OR eseguita tra una serie di bit (tra cui anche quello generato dalla NLF) e ancora più sotto il registro a 64 bit che contiene la chiave per la crittografia, ricavata attraverso i passaggi visti e descritti nell’articolo "Algoritmo di crittografia della codifica RollingCode".
Ora che abbiamo chiaro quali sono i dati che sono necessari per eseguire la decrittografia, possiamo procedere con la spiegazione per punti dell’algoritmo:
1. Come prima cosa devono essere prelevati i bit 0, 8, 19, 25 e 30 dal codice a 32 bit criptato, per andare a costruire una word formata da 5 bit.
2. La word a 5 bit precedentemente ricavata, deve essere sottoposta in ingresso alla NLF la quale fornirà in uscita un solo bit che sarà funzione dei valori dati in ingresso.
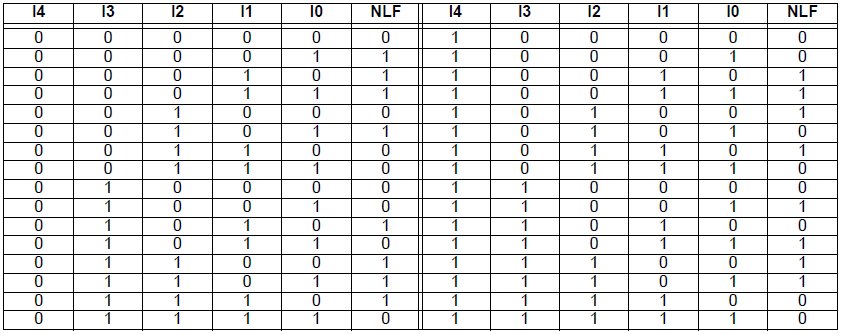
le colonne “I4”, “I3”, “I2”, “I1” e “I0” corrispondono rispettivamente ai bit 30, 25, 19, 8 e 0 del codice criptato, mentre “NLF” rappresenta il bit di uscita della funzione.
Riprendendo l’esempio precedente avremo che dalla word “
3. Ora che si ha a disposizione il bit dalla “NLF” occorre sottoporlo ad una operazione di OR con il bit 31 della parola criptata e con il bit 15 della chiave di crittografia, in modo da ottenere un ulteriore bit risultato dell’operazione.
4. Dopo aver ricavato il bit di uscita dall’operazione di OR, deve essere eseguito uno shift di un bit verso sinistra (verso il bit più significativo) della parola criptata.
5. Una volta eseguito lo shift, deve essere eseguita un’operazione di sostituzione del bit 0 della parola appena shiftata, con il bit risultato dell’operazione di OR ricavato nel passo “
6. Un’ultima operazione da eseguire è quella di eseguire una rotazione verso sinistra (verso il bit più significativo) della chiave usata per la crittografia.
7. I punti dall’ “
Alla fine dei 66 cicli sulla parola a 32 bit che è presente il valore decriptato e pronto ad essere utilizzato.
Lettura consigliata: Introduzione alla codifica RollingCode







