Se c’è una cosa che facciamo di continuo è contare, certe volte senza neanche rendercene conto. Contare è spesso e volentieri così difficile e noioso che non ci va di farlo di persona, e ci rivolgiamo a qualche sistema che lo faccia per noi. Ma ci sono così tante cose da contare negli ambiti più disparati che è difficile pensare di poter fare tutto con lo stesso dispositivo. Oggi vi parleremo di come si possano contare i giri di una ruota senza intervenire direttamente su di essa e di come la tecnologia di oggi possa venirvi in soccorso.
FACCIAMO DUE CONTI
Contare è una delle prime cose che ci insegnano quando siamo piccoli. Si parte dai numeri e si parte con le caramelle, ed è un qualcosa che ha subito un riscontro pratico: adesso finalmente possiamo controllare che il fratellino non ci rubi quelle gommose che ci piacciono tanto! Poi si passa alle fette di torta, che è un modo perfetto per spiegare le frazioni (oltre che per cercare di prendersi il pezzo più grosso). Poi ancora tocca a cose più particolari, come pi greco o la radice di due, quando ti distruggono una delle certezze della vita facendoti capire che in realtà ci sono cose che non si possono contare.
Si procede per un po’ così, e di pari passo ti insegnano metodi sempre più raffinati per farlo. Si parte con le tabelline (uff…), si prosegue con le espressioni e si sfocia nelle equazioni. Per quelli che hanno la sciagurata idea di proseguire su questa strada, ci si addentra nel calcolo di infiniti e infinitesimi, con qualche deviazione su terreni un po’ più singolari come il conteggio di quante frazioni esistano, o di quanti siano i punti su una retta, cose di questo genere. Il percorso si fa sempre più erto e irto di difficoltà e dimensioni, che da una diventano due e tre e talvolta n. Il concetto, ti spiegano, in fin dei conti è sempre quello, solo esteso a casi più generali. Ti fanno capire come la matematica sia solo un modo per applicare un concetto a quanti più casi possibile. I matematici sono pigri, non dimentichiamocelo mai!
Ma se sei arrivato a lavorare su volumi e superfici e spazi a n dimensioni, probabilmente non hai nemmeno voglia di farlo. Vuoi le applicazioni, non le formule; vuoi la pratica, e non la teoria. Per tua fortuna di lì a poco iniziano a farti vedere come realizzare circuiti per contare. Parti da dei semplici circuiti contatori e poi scopri come puoi utilizzare un microcontrollore per lo stesso scopo, sprecando un’infinità di risorse in più ma risparmiando anche un’infinità di tempo, fatica e capelli.
Contare degli eventi nel mondo digitale è facile: bastano dei flip-flop. Contare degli eventi nel mondo analogico è un po’ più complicato: ci servono almeno dei comparatori ed eventualmente qualche meccanismo per impostare le soglie. Nel complesso, si tratta di qualche componente e un po’ di fili, e alla fine dei conti è fattibile, se potete mettere mano alla ruota. Ma se non potete? O se potreste ma non è il caso di farlo?
RUOTE CHE GIRANO
Immaginiamo di voler contare i giri di una ruota. Se avete accesso alla ruota, è piuttosto semplice e lo potete fare in tanti modi diversi. Avete mai montato il contachilometri su una bicicletta? Tipo quello nella Figura 1. Dovete installare tre affarini, uno sulla ruota, uno sulla forcella e uno sul manubrio. Sulla forcella c’è il trasmettitore, ad esempio un fotodiodo. Sulla ruota c’è il ricevitore. Per esempio potreste mettere un fototransistor, ma sulla ruota di una bicicletta non è il caso di aggrovigliare dei fili, quindi magari mettete sulla ruota uno specchietto e il fototransistor sulla forcella, accanto al fotodiodo. Quando lo specchietto passa davanti al fotodiodo, il fototransistor legge un impulso e il microcontrollore nel terzo affarino sul manubrio conterà un giro. Note le dimensioni della ruota, si possono ricavare i chilometri percorsi.
Con i sensori ottici si possono fare anche cose più sofisticate, ad esempio capire a che punto della rotazione si trova la ruota. Ricordate i mouse a pallina? Quelli che ogni tanto dovevate smontare e pulire perché sennò non si muovevano più? Bene, quelli al loro interno avevano due encoder ottici. Un encoder ottico è una ruota con una serie di spazi che fanno passare la luce e con una serie di aree chiuse che la bloccano. Una cosa psichedelica come quella nella Figura 2. A seconda della posizione della ruota, il ricevitore non legge banalmente 1 (il sensore è davanti al trasmettitore) o 0 (il sensore è chissà dove), ma un numero binario che ci dice a che punto della rotazione siamo arrivati. Ad esempio, un encoder a tre bit divide il cerchio in otto settori, e la posizione avrà quindi un’accuratezza di 360/8 = 45 gradi. Muovendo il mouse a destra e a sinistra si fa ruotare la pallina, che a sua volta fa girare un asse collegato alla ruota dell’encoder. Il microcontrollore nel mouse legge gli encoder e ricava lo spostamento in orizzontale e/o in verticale avvenuto dall’ultima lettura, e il gioco è fatto.
I sensori ottici sono molto comodi per queste cose, ma non è detto che si possano sempre usare. Immaginate che la vostra ruota si trovi dentro un tubo, per esempio un tubo che trasporta gas o acqua. La ruota, in quel caso, lavora da sensore per la misura del volume di gas o acqua trasportati o consumati. Quanto più gas o acqua circolano, tanti più giri compirà la ruota. Potreste ovviamente installare dei sensori ottici su queste ruote, ma dovreste bucare il tubo per far passare i fili, e se anche decideste di utilizzare un sistema wireless, comunque dovreste garantire che il sensore e il trasmettitore siano in grado di resistere all’acqua o al gas che circolano nel tubo. È sicuramente fattibile, ma quanto è difficile! Come i matematici, anche gli ingegneri sono pigri: non ci piacciono le complicazioni inutili.
TUTTO E’ POSSIBILE CON I SENSORI INDUTTIVI
Torniamo alla faccenda della ruota della bicicletta, e immaginiamo di sostituire il sensore ottico con un sensore di prossimità induttivo. Si tratta di una cosa sensata, se ci pensate: il giochetto con lo specchietto funziona, ma è comunque un po’ problematico. Si deve allineare per bene lo specchio, altrimenti la luce emessa non lo raggiungerà, o quella riflessa non raggiungerà il ricevitore, e del resto basta uno scossone un po’ forte per disallinearlo. Sostanzialmente, dopo un po’ di buche è possibile che il contachilometri non conti più. Un sensore di prossimità induttivo, invece, misura la perturbazione del campo magnetico generato da un induttore quando ci si fa passare in mezzo un pezzetto di materiale ferromagnetico. Quanto più il pezzetto di materiale ferromagnetico è vicino all’induttore, tanto più perturbato sarà il campo. Piazzando una soglia ad un livello opportuno, si può far scattare il contatore solo ed esclusivamente quando il ricevitore passa davanti al trasmettitore. I sensori induttivi sono immuni alle interferenze (scattano solo se ci sono materiali ferromagnetici nelle vicinanze), allo sporco e agli scossoni, e sono anche piuttosto robusti: l’ideale per un contachilometri! Ancora, i sensori induttivi sono totalmente insensibili a qualsiasi materiale nei paraggi che non sia ferromagnetico. Plastica, legno, cemento, anche l’acciaio inox sono totalmente trasparenti per sensori del genere.
Un sensore di questo tipo però è binario: o la lettura è sopra soglia, o non lo è. O il ricevitore è davanti al trasmettitore, o non lo è. Così su due piedi non possiamo prendere questo sistema e renderlo l’equivalente induttivo dell’encoder ottico. Non abbiamo modo cioè di sapere anche a che punto della rotazione ci troviamo. Per fare questo, dobbiamo (purtroppo o per fortuna, come preferite) complicarci un po’ la vita.
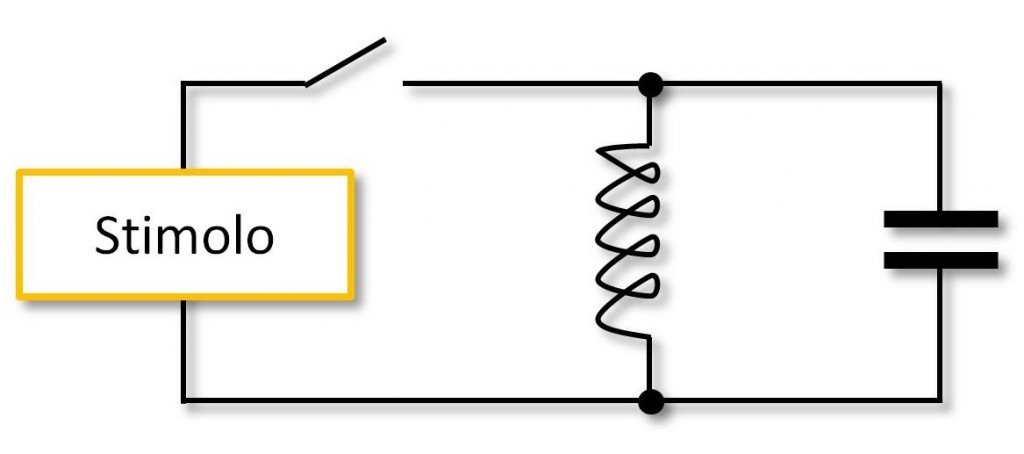
Aggiungiamo un condensatore in parallelo all’induttore, come nella Figura 3. Abbiamo il più classico dei circuiti risonanti, quello in cui, una volta stimolati, induttore e condensatore si rimpallano l’energia all’infinito, e il circuito oscillerà per i secoli dei secoli amen. È anche uno dei circuiti più odiati dagli studenti di ingegneria di tutto il mondo, perché è quello con il quale di solito ti fanno conoscere (e risolvere) le equazioni differenziali del secondo ordine, in tutte le salse possibili: con attenuazione e senza, con stimolo iniziale e senza. Dell’infinità di conti che ti hanno fatto fare (sempre conti!) di massima quello che resta è che la frequenza di oscillazione è, nel caso ideale:
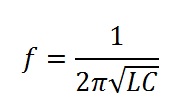 e che nel caso reale queste oscillazioni non vanno avanti in eterno, ma pian piano si attenuano, perché le resistenze interne dei componenti (soprattutto la resistenza dovuta ai fili con cui sono stati realizzati gli avvolgimenti dell’induttore) dissipano potenza. Le perdite di solito vengono quantificate mediante il fattore Q dell’induttore:
e che nel caso reale queste oscillazioni non vanno avanti in eterno, ma pian piano si attenuano, perché le resistenze interne dei componenti (soprattutto la resistenza dovuta ai fili con cui sono stati realizzati gli avvolgimenti dell’induttore) dissipano potenza. Le perdite di solito vengono quantificate mediante il fattore Q dell’induttore:
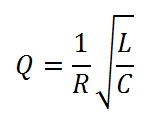 Quanto più sono basse le perdite (quanto più è bassa la R nella formula), tanto più è “buono” l’induttore, ossia tanto più vicino all’idealità sarà l’induttore, e tanto più a lungo il circuito oscillerà prima di smorzarsi.
Quanto più sono basse le perdite (quanto più è bassa la R nella formula), tanto più è “buono” l’induttore, ossia tanto più vicino all’idealità sarà l’induttore, e tanto più a lungo il circuito oscillerà prima di smorzarsi.
Ok, e quindi? Il sensore induttivo è in grado di rilevare il materiale ferromagnetico fondamentalmente perché quest’ultimo assorbe parte del campo magnetico generato dall’induttore. Più il ricevitore è vicino al trasmettitore, più campo assorbirà. Quindi, se facciamo girare la nostra ruota vicino ad un circuito risonante, le perdite del circuito aumenteranno man mano che il ricevitore si avvicina al trasmettitore,e diminuiranno man mano che si allontana. Quindi, man mano che il ricevitore si avvicina al trasmettitore, il fattore di qualità scende, e l’oscillazione si smorza prima. Quindi, se riuscissimo a misurare il numero di oscillazioni che compie il circuito e se ripetessimo questa misura più velocemente di quanto la ruota giri, potremmo sapere, a seconda del conteggio ottenuto, a che punto della rotazione ci troviamo.
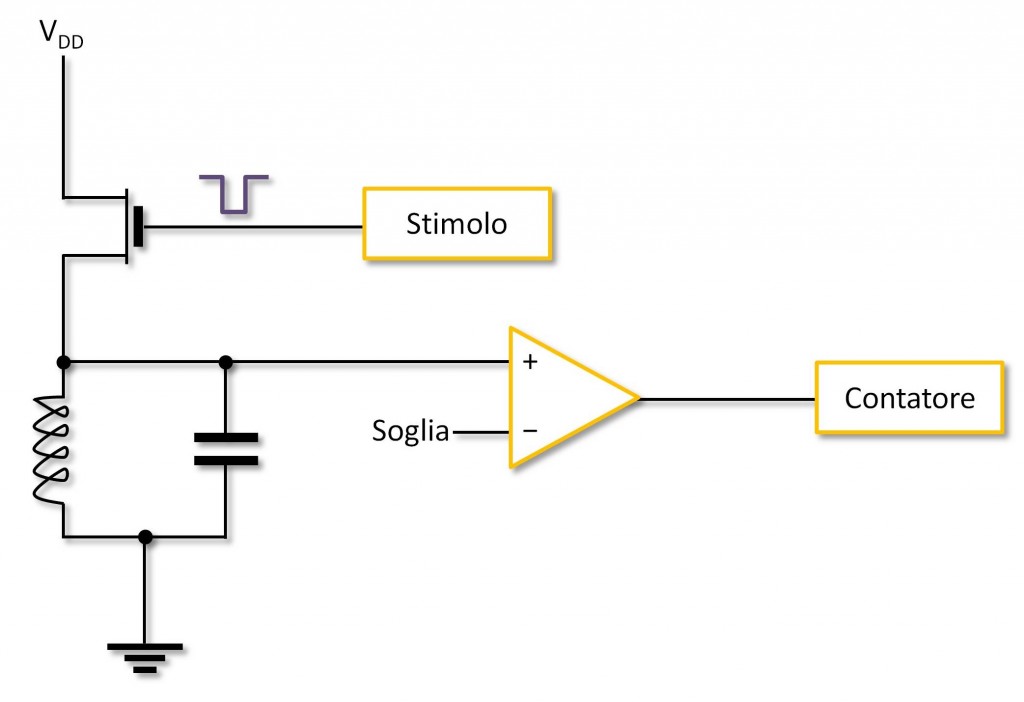
Uhm... Non sembra una cosa tanto semplice. Ci servono parecchie cose. “Contare le oscillazioni prima che queste si siano smorzate oltre un certo tot” equivale a contare i picchi della sinusoide generata dal risonatore che superano una certa soglia. Ci serve quindi un comparatore con soglia, che generi un impulso ogni volta che la soglia viene superata; ci serve un accumulatore, che venga incrementato di uno ogni volta che viene generato un impulso; e ci serve un sistema per eccitare il circuito risonante. Il circuito risuona ad una particolare frequenza, e solo a quella se il Q è sufficientemente alto, e lo si eccita pilotandolo con una sinusoide a quella particolare frequenza. Tuttavia, la frequenza di questa sinusoide cambia con i componenti che scegliamo di utilizzare, il che significa che utilizzare un oscillatore sinusoidale come stimolo non è granché come idea, a meno che non sia un VCO, ossia un oscillatore a cui possiamo cambiare la frequenza mediante un controllo in tensione. Un VCO non è un circuito propriamente semplice da progettare (anche se potete ovviamente trovarne in commercio alcuni già pronti), e il controllo in tensione comunque prevede una conversione D/A ed eventualmente altra circuiteria di condizionamento. No, molto più semplice è eccitare il circuito mediante un impulso rettangolare. Come la trasformata di Fourier c’insegna, lo spettro di un impulso rettangolare ha banda infinita, il che significa che un impulso rettangolare è in grado di eccitare tutte le frequenze contemporaneamente. Sarà poi la selettività del circuito risonante (ecco perché ci serve un Q bello alto, oltre che per il problema delle perdite) a far sì che si oscilli ad una e una sola particolare frequenza. Alla fine della festa, ci serve un circuito come quello della Figura 4.
Dunque adesso dobbiamo metterci a progettare tutta questa robaccia? Fortunatamente no! La Silicon Labs produce dei microcontrollori a 32 bit, della famiglia SiM3L1xx, che al loro interno contengono un modulo dedicato, l’Advanced Capture Counter (ACC), che tra le altre cose può essere utilizzato esattamente per un’applicazione di questo tipo. L’ACC contiene sia il generatore di stimolo, che l’accumulatore, che la circuiteria per la misura.
[...]
ATTENZIONE: quello che hai appena letto è solo un estratto, l'Articolo Tecnico completo è composto da ben 2811 parole ed è riservato agli ABBONATI. Con l'Abbonamento avrai anche accesso a tutti gli altri Articoli Tecnici che potrai leggere in formato PDF per un anno. ABBONATI ORA, è semplice e sicuro.