Dopo aver parlato, nei due precedenti articoli, della trasformata di Fourier e della trasformata Z, non potevamo non occuparci di un'altra importantissima trasformata ampiamente utilizzata in ambito scientifico e tecnologico: quella di Laplace. Benché venga chiamata così in onore di Pierre Simon Laplace (in quanto la utilizzò nei suoi studi riguardanti la teoria della probabilità), essa in realtà venne sviluppata da Eulero. Tra le sue numerose applicazioni, vi sono: la risoluzione di equazioni integro-differenziali, l’analisi dei circuiti e l'elaborazione dei segnali. In questo articolo, mostreremo in che modo con la trasformata di Laplace sia possibile, ad esempio, studiare gli effetti dei carichi sulle travi e determinare il comportamento di un circuito elettrico. Vedremo inoltre come essa, grazie al software MATLAB, possa essere calcolata facilmente anche da chi non possiede elevate competenze matematiche.

1 Definizione

Sia f(t) una funzione a valori reali o complessi definita (almeno) sul semiasse reale non negativo (t ≥ 0). Si dice che f è trasformabile secondo Laplace (o L-trasformabile) se esiste un numero complesso s tale che la funzione (di t) e^-stf(t) sia sommabile su [0, +∞), ossia tale che:

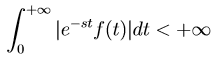ovvero, se ci riferiamo all'integrabilità secondo Lebesgue, tale che: e^-stf(t) ∈ L¹([0, +∞)). In tal caso, l'integrale

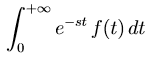è ben definito e prende il nome di integrale di Laplace. Se e^-stf(t) è sommabile su [0, +∞) per un certo valore complesso s₀, allora lo è per ogni s ∈ C tale che Re(s) > Re(s₀); infatti:

|e^-stf(t)| = |e^{-[Re(s) + iIm(s)]t}f(t)| = |e^-Re(s)t||e^{- iIm(s)t}||f(t)| = e^-Re(s)t|f(t)| ≤ e^-Re(s₀)t|f(t)| = |e^-s₀tf(t)|

e pertanto e^-stf(t), essendo maggiorata in modulo da una funzione sommabile su [0, +∞), è anch'essa sommabile su [0, +∞).

Da ciò si evince che l'insieme dei valori di s che rendono sommabile e^-stf(t) su [0, +∞), se non è vuoto, è costituito da tutti i numeri complessi la cui parte reale è maggiore di un valore che viene indicato con σ[f] e prende il nome di ascissa di convergenza di f. I punti corrispondenti a tali numeri complessi sono ovviamente quelli del semipiano destro individuato dalla retta x = σ[f], detti rispettivamente semipiano di convergenza e retta di convergenza.

L'integrale di Laplace di una funzione L-trasformabile f(t) è dunque una funzione definita in {s ∈ C | Re(s) > σ[f]}; essa viene chiamata trasformata di Laplace e si indica con

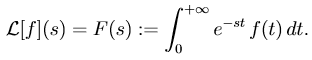È evidente che la trasformata di Laplace rientra nella categoria delle trasformate integrali. Il suo nucleo integrale è ovviamente e^-st.

1.1 La trasformata bilatera di Laplace

Se f(t) è definita su tutto R ed è tale che e^-stf(t) ∈ L¹(R) per certi valori di s, è possibile definire la trasformata bilatera di Laplace di f(t):

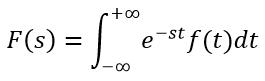Per determinare il dominio di F(s) (ovvero il sottoinsieme di C che rende sommabile e^-stf(t) su R), consideriamo le seguenti funzioni definite solo per t > 0:

e indichiamo con F₊(s) e F_-(s) le loro rispettive trasformate di Laplace (unilatere). Si ha:

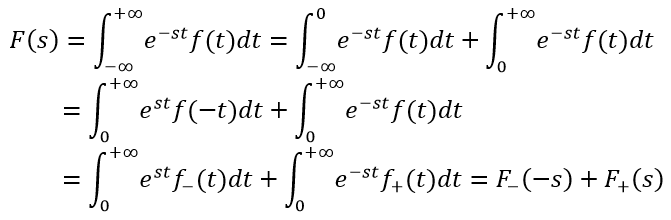Pertanto, il dominio di F(s) è l'intersezione dei domini di F₊(s) e F_-(-s):

{s ∈ C | Re(s) > σ[f₊]}∩{s ∈ C | Re(-s) > σ[f_-]} = {s ∈ C | Re(s) > σ[f₊]}∩{s ∈ C | Re(s) < -σ[f_-]} = {s ∈ C | σ[f₊] < Re(s) < -σ[f_-]}

e quindi la trasformata bilatera di f esiste soltanto se [...]

ATTENZIONE: quello che hai appena letto è solo un estratto, l'Articolo Tecnico completo è composto da ben 2570 parole ed è riservato agli ABBONATI. Con l'Abbonamento avrai anche accesso a tutti gli altri Articoli Tecnici che potrai leggere in formato PDF per un anno. ABBONATI ORA, è semplice e sicuro.

Ti potrebbe interessare anche:

Costruiamo un robottino in LEGO – Applicazioni

Elettronica di potenza ed Intelligenza Artificiale: un matrimonio perfetto

Firmware 2.0 #15 – Open Source IoT/Blockchain

Firmware 2.0 #44: Medical/Wearable

Scopriamo la piattaforma SensorTile.box: programmare con ST BLE Sensor

Firmware 2.0 #06 – Industry 4.0/Smart Projects