
Per poter effettivamente valutare le radiazioni dei campi, così come evidenziato nelle Figure dell'articolo Le radiazioni delle antenne, bisogna distinguere due momenti di studio: quello su campi vicini e quello su campi lontani. Questo si rende necessario perché le due situazioni presentano una differenza sostanziale che consiste, essenzialmente, nel fatto che in prossimità della sorgente irradiante, cioè in condizioni di campo vicino, il campo elettrico ed il campo magnetico assumono rapporti variabili con la distanza; ad una certa distanza, invece, cioè in condizioni di campo lontano, il rapporto tra campo elettrico e campo magnetico rimane costante.
Per studiare la radiazione di campi vicini, possiamo pensare alle antenne delle Stazioni Radio Base come vettori di dipoli risonanti a mezz’onda, ovvero antenne realizzate a partire da un conduttore lungo λ e ripiegato in modo tale da dare luogo ad un’antenna lunga λ/2. La corrente nei due tratti di conduttore è la stessa. Per calcolare l’intensità di potenza media, consideriamo un sistema di riferimento in coordinate cilindriche (come nelle figure precedenti, il sistema di riferimento è O(ρ,φ,z)) e scriviamo:
Pd=12L-LL12ReEzρ,zHϕ*ρ,zdz
che altro non è che il modulo del Vettore di Poynting, misurato in [W/m2], ed in cui E ed H sono, rispettivamente, le componenti che corrispondono ai valori massimi dei campi elettrico e magnetico.
La potenza media può essere espressa, anche, dalla:
Pd= N Prad2πρ2L
in cui N indica il numero di canali, ovvero delle portanti modulate.
In prima approssimazione, la potenza media può essere espressa come:
Pdρ, ϕ<γ;L=N Prad2πρ2L1+ρρ02
ρ0=γπGAL
in cui ρ è la distanza alla quale ci troviamo dall’antenna, 2L è la lunghezza dell’antenna stessa, GA il suo guadagno ed il fattore γ rappresenta la semi-apertura del riflettore.
Qualora il valore limite dell’esposizione alla densità di potenza fosse noto a partire dall’espressione della distanza critica per l’esposizione alla radiazione GSM, esso potrebbe essere determinato direttamente dalla relazione precedente. Infatti risulta che:
ρ2=12ρ0ρ02+NPradPd1γ2L2-ρ0
Considerando, poi, il modello della radiazione realizzata nel piano orizzontale si ha:
Pdρ, ϕ<γ;L=N Prad2πρ2L1+ρρ02e-ln2ϕϕ2
ρ0=γ8πGAL
in cui il termine 2φ rappresenta i -3 dB dell’ampiezza orizzontale del raggio.
La densità media di potenza, ed il valore quadratico medio (ovvero, il valore efficace), del campo elettrico sono dipendenti tra loro a mezzo della impedenza di spazio libero. Infatti si scrive:
Pd=E2Z0
Passiamo, quindi, alla valutazione dei campi lontani. Vista la premessa di cui sopra, utilizzeremo i principi dell’ottica geometrica per determinare l’ampiezza del campo. Il campo elettrico ha due componenti: una incidente
Ein=E0(ϕ,ϑ)re-jβr
ed una riflessa
Er=ΓR(ϕ,ϑ)E0(ϕ',ϑ')r'e-jβr
in cui ΓR non è altro che il coefficiente di riflessione corrispondente ed E0 l’ampiezza dell’onda incidente definita come:
E0ϕ,ϑ=30NPradG(ϕ,ϑ)
dove G(ϕ,ϑ) è il modello di radiazione per la particolare antenna oggetto dello studio.
Dalla composizione delle due componenti ricaviamo l’entità del campo elettrico totale, cioè si ha:
Etot=Ein+Er
Sfruttando, ora, il concetto di potenza equivalente irradiata isotropicamente (EIRP) possiamo esprimere il campo totale come:
Etotr,θ,φ=Z0Htotr,θ,φ=230NPradG(ϕ,ϑ)r=230N EIRPr
in cui il fattore 2 è introdotto per tenere in conto del caso in cui si abbia perfetta riflessione del fronte d’onda piana al suolo.
È possibile, in alternativa a questo approccio, valutare il campo elettrico irradiato da un’antenna BTS in base al calcolo della densità di potenza. Infatti, si può scrivere:
Pd=PtGt4πr2=EIRP4πr2
Se assumiamo, inoltre, di voler valutare la medesima quantità in una regione, questa volta, di campo vicino, si può considerare una doppia riflessione della densità di potenza entrante. Prendendo, quindi, in considerazione tutti i fenomeni di riflessione, si ha:
Pd=PtGtπr2=PGπr2=EIRPπr2
ovvero ne risulta un incremento qualitativo di 4 volte. In particolare, approssimando la forza di campo a livello del suolo e la relativa densità di potenza ottenuta supponendo l’incremento massimo nelle riflessioni pari al 65%, la potenza media viene scalata di un fattore 2,7225 (1,652) e si ha:
Pd=2.7225 EIRP4πr2=0.68EIRPπr2
Questa equazione può essere utilizzata per studiare sia antenne omnidirezionali sia vettori direzionali. Di contro, l’uso di questa equazione fornisce una sovrastima del campo in un punto generico. Pertanto, per ottenere valori più accurati ed attendibili del campo, qualora si conosca il modello di radiazione d’antenna, esso può essere inserito e se ne può tenere conto nei calcoli. Se si conosce, dunque, il guadagno numerico, si ha:
Pd=2.7225 EIRP4πr2=0.68EIRPπr2Fϕ,ϑ
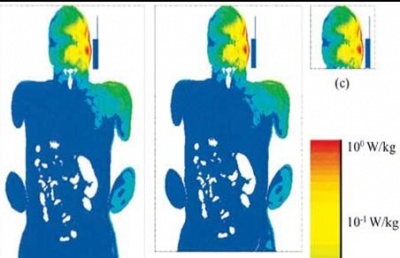
Come già detto, l’incremento della richiesta di copertura, dovuto all’aumento del numero delle utenze, ha portato all’installazione di nuove antenne BTS con conseguente aumento della preoccupazione, da parte degli utenti, in merito alla possibilità di danni alla salute, soprattutto per chi vive in prossimità dei siti utilizzati per l’installazione.
Al fine di garantire le condizioni di sicurezza, che verranno definite in termini numerici nel prossimo paragrafo, intorno all'antenna viene sempre definita un'area, detta zona di rispetto, che può essere rappresentata in maniera schematica con un parallelepipedo le cui dimensioni sono dell'ordine di pochi metri. All'interno di tale zona viene impedito l'accesso della popolazione mentre al di fuori di essa si è sicuramente in condizione di pieno rispetto della normativa.
Essendo, quindi, le dimensioni di tale zona molto ridotte, anche nel caso in cui l'antenna sia sul tetto di una abitazione, il campo a cui si è esposti all'interno (in caso di condominio anche l'appartamento dell'ultimo piano) e nelle abitazioni vicine è sicuramente molto inferiore al limite di sicurezza. Questo anche a causa della legge per cui decresce l'intensità di campo allontanandosi dall'antenna.
La distanza di sicurezza da un’antenna, definita proprio in funzione della zona di rispetto, e da ora indicata come dmin, può essere ricavata dall’espressione della densità di potenza; infatti si ha:
Pd=N Pt10Gt-L104πr2
dove Gt è il guadagno d’antenna espresso in decibel, Pt è la massima potenza trasmessa, il termine L rappresenta, come già detto, le perdite ohmiche, ed N è il numero dei trasmettitori; la distanza di sicurezza da un sistema di antenna è espressa da:
dmin=N Pt10Gt-L104Pdmax
in cui Pd rappresenta la massima densità di potenza che è permessa nell’aria, misurata in W/m3, dagli standard di sicurezza per l’intervallo di frequenze in esame.
L'indice completo degli articoli relativi alla tesi di laurea sulla interazioni e sugli effetti delle radiazioni sul corpo umano, è disponibile qui





Questo rimane valido in teoria nella pratica visto che per decenni ho visto come si faceva a trasmettere in Per la radiodiffusione.
Impianti di antenna non si strutturano mai con una sola antenna ma di solito con quattro antenne una sopra l’altro in modo da ridurre il fascio il più possibile,
Con l’obiettivo di passare con un cono di diffusione di 45° a 12.5° e quello più comune.
per questo di solito si mettono quattro di polli accodati tra di loro in altezza.
È chi posso garantire che il campo elettrico può cambiare moltissimo.
La cosa interessante è che sotto il palo di trasmissione visto che le guide donde erano perfettamente stagno elettromagnetica mente, e chi trasmettitori anche se erano completamente smontati aperti e fugavano dappertutto come comizio già spiegato in un altro post, rimanevano chiusi sottoterra con una schermatura dovuto sia al doppio reticolo dell’intelaiatura di cemento armato sia dal metro di terra soprastante.
quindi torniamo a sotto l’antenna spesso il segnale era piuttosto zero, è si faceva grandi difficoltà a sintonizzare una radio. e dentro l’analizzatore di spettri la cosa più strana cosa sotto l’attore era quasi in calma piatto ma se camminavamo per 1 km e gli facevamo le misure e dirige l’esito di spettri cresceva una stecca di rumore in circa il 40 dB.
Nella realtà dei fatti con le antenne è molto difficile fare calcoli preventivi, esperienza ventennale visto che al momento del posizionamento che ritrovi tutti i calcoli tuoi sballati, i fenomeni molto strani uno dei fenomeni più interessanti invertendo i cari tra le diverse antenne messe uno sopra l’altro si può ottenere un campo magnetico nulla giocando con le fasi delle antenne e tuttavia dal rilevatore del amplificatore finale ( si consuma e chi spedisce in aria 1 Kw RMS.
Ma la cosa che mi stupisce sempre è il fatto che si parla moltissimo della banda che si trovanella zona non ionizzanti dove non si è dimostrato ancora nulla per certezza di studi si accavallano uno sopra l’altro che si dimezzano vicenda, riguarda la Banda ionizzanti qui nessuno se ne preoccupa, sapendo benissimo che provocano con certezza i tumori.
Infine non si parla mai di campi magnetici continui che anche quelli con tantissimi studi sono stati dimostrati Che provocano i tumori con certezza, ma il fatto sicuramente che l’unico luogo dove si possono trovare tali campi magnetici sia proprio l’ospedale con una risonanza magnetica si possono ottenere campi che va 1T a 5T senza nessun problema, in questi due ultimi casi nessuno apre bocca