La recente introduzione di potenti e versatili strumenti per lo sviluppo di applicazioni deep learning ha semplificato notevolmente l’implementazione dei layer convoluzionali all’interno dei modelli di rete neurale. Tuttavia, il concetto di convoluzione può risultare per molti oscuro o poco chiaro: l’obiettivo dell’articolo è quello di fare chiarezza su questo argomento, mostrando come un approccio step by step possa aiutare alla comprensione di questa importante classe di reti neurali, caratterizzata da fascino, potenza ed estensibilità.
Introduzione
Le reti neurali convoluzionali, indicate in letteratura con gli acronimi CNN (Convolutional Neural Network) o ConvNet, rappresentano senza alcun dubbio una delle più importanti categorie di reti neurali utilizzate nel deep learning. Le ConvNet sono ad esempio utilizzate in applicazioni di riconoscimento delle immagini, analisi e riconoscimento del segnale audio, interpretazione della scrittura e classificazione di oggetti. Tuttavia, la comprensione del concetto di convoluzione, soprattutto inizialmente, può risultare leggermente frustrante, con termini come filtri, kernel e canali che si susseguono in rapida sequenza. In realtà la convoluzione è un connubio di fascino e potenza con applicazioni nel campo del riconoscimento di oggetti, volti, segnali stradali e sistemi per la visione artificiale nei robot e nelle auto a guida autonoma. In Figura 1 possiamo ad esempio osservare come una ConvNet sia in grado di identificare e riconoscere tramite classificazione varie tipologie di cartelli stradali, mentre in Figura 2 essa sia in grado di analizzare le scene relative a un evento sportivo, suggerendo un’informazione molto accurata riguardo gli oggetti riconosciuti (un guantone da baseball e due giocatori, in questo caso).
In precedenti articoli abbiamo già introdotto alcuni concetti fondamentali relativi alle reti neurali e in particolare il modello di neurone artificiale, o percettrone (perceptron). Abbiamo già visto in cosa consistano gli hidden layer (layer di percettroni posti tra il layer di ingresso e quello di uscita della rete neurale) e i fully connected layer (layer di percettroni interamente connessi tra loro). Per la comprensione dei nuovi concetti che introdurremo nel corso dell'articolo sono sufficienti conoscenze basilari di algebra.
L’architettura LeNet
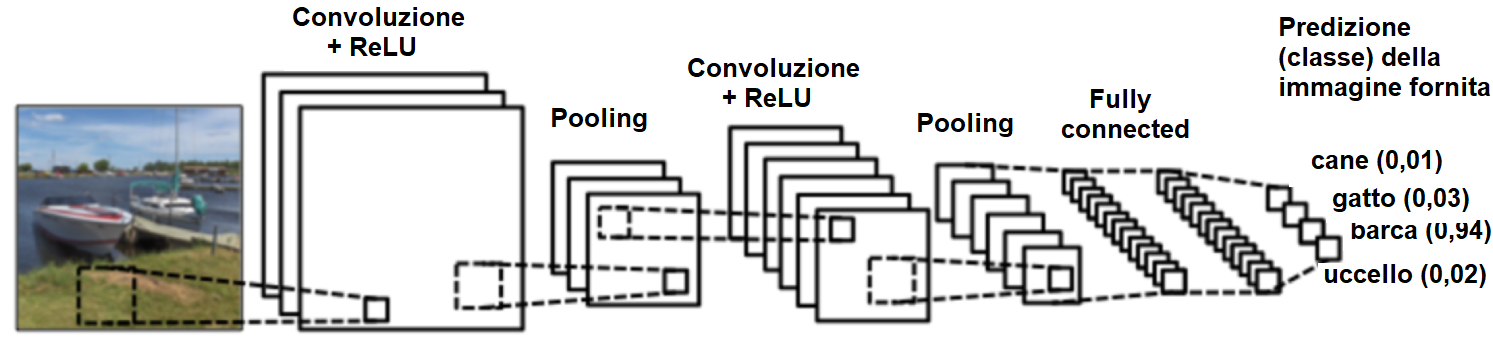
Parlando di ConvNet, non si può prescindere dal fare un cenno all’architettura LeNet, non fosse altro per motivi di carattere storico. LeNet è infatti una delle prime reti neurali convoluzionali, introdotta negli anni ’90 da Yann LeCun e inizialmente applicata al riconoscimento dei caratteri (cifre decimali e codici di avviamento postale, per l’esattezza). L’architettura LeNet rappresenta una pietra miliare nel campo dell’intelligenza artificiale, avendo contribuito significativamente alla diffusione e al successo del deep learning. Le più recenti architetture attualmente utilizzate nel riconoscimento di immagini possono essere considerate un’evoluzione dell’architettura LeNet e in esse si possono ancora riconoscere i componenti principali del modello originale. In Figura 3 possiamo osservare una ConvNet basata sull’architettura LeNet, utilizzata per classificare l'immagine fornita in ingresso in quattro categorie: cane, gatto, barca oppure uccello. Alimentando la rete neurale con l’immagine di una barca (si osservi la parte più a sinistra di Figura 3) la rete esegue correttamente il riconoscimento, assegnando, tra tutte le possibili categorie, la probabilità più elevata (pari 0,94, quindi molto vicina al valore massimo 1 corrispondente all’assoluta certezza) all’oggetto barca. Come vedremo tra poco, la somma di tutte le probabilità ottenute nel layer di uscita deve essere pari a uno.
Per comprendere il funzionamento delle ConvNet dovremo anzitutto assimilare i seguenti concetti, riscontrabili in ogni rete neurale di questo tipo (inclusa quella di Figura 3):
- convoluzione
- non linearità, indicata in letteratura con il termine ReLU
- pooling o sotto campionamento
- classificazione (a sua volta legata al concetto di layer completamente connesso, o fully connected layer).
Rappresentazione delle immagini
Sappiamo che ogni immagine, di qualunque tipo essa sia, può essere sempre ricondotta a una matrice di pixel (in Figura 4 possiamo osservare il particolare ingrandito di un’immagine, con evidenziati i singoli pixel). Nel caso particolare di immagine a colori, possiamo poi parlare di canale, dove per canale si intende un componente di base dell’immagine. I tre canali che compongono l’immagine (rosso, verde e blu) non sono altro che tre matrici bidimensionali sovrapposte, in cui ogni pixel è rappresentato tramite un byte (valori compresi tra 0 e 255). Nel caso invece di immagine in bianco e nero avremo un solo canale e quindi una sola matrice bidimensionale in cui ogni singolo pixel può assumere i valori compresi tra 0 (corrispondente al nero) e 255 (corrispondente al bianco). Per semplicità, nel corso dell’articolo faremo riferimento esclusivamente ad immagini in bianco e nero.
Convoluzione
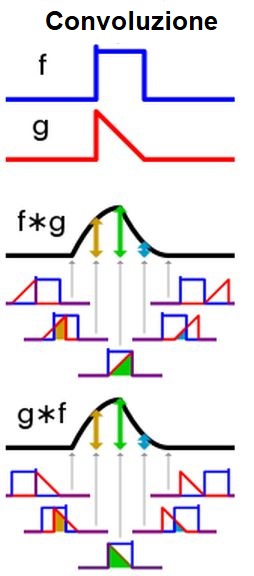
Con il termine convoluzione si intende un operatore matematico che esegue l’integrale del prodotto tra due funzioni, una delle quali viene capovolta di 180° rispetto all’asse verticale prima di eseguire il prodotto. Come visibile in Figura 5, riferita al caso di due funzioni f(t) e g(t), la prima cosa da fare è ruotare orizzontalmente di 180° il segnale g. Successivamente, si lascia scorrere il segnale g capovolto sul segnale f, moltiplicando e sommando i valori così ottenuti. L’ordine dei segnali non influisce sul risultato della convoluzione, cioè conv(a,b) è identicamente uguale a conv(b,a). Il segnale di colore blu in Figura 5 rappresenta il segnale in ingresso, mentre il segnale di colore rosso (g(t)) viene anche detto kernel o filtro. L’operazione di convoluzione è largamente impiegata negli algoritmi di elaborazione dei segnali: filtraggio del segnale audio in una dimensione, filtraggio delle immagini in due dimensioni (il caso che approfondiremo ora) e ricerca di particolari pattern all’interno dei segnali sono solo alcuni esempi di possibili applicazioni.
In Figura 6 possiamo osservare il risultato della convoluzione tra un impulso rettangolo (f) e uno triangolare (g). Si noti l’invarianza del risultato rispetto all’ordine dei due segnali.
Applicata alle reti neurali ConvNet, la convoluzione ha il compito di estrarre le “feature”, in sostanza delle specifiche caratteristiche, dall’immagine in ingresso. Questo è il motivo per cui, come indicato in Figura 3, il layer convoluzionale è il primo in ogni rete con architettura ConvNet. La convoluzione presenta l’importante proprietà di [...]
ATTENZIONE: quello che hai appena letto è solo un estratto, l'Articolo Tecnico completo è composto da ben 2905 parole ed è riservato agli ABBONATI. Con l'Abbonamento avrai anche accesso a tutti gli altri Articoli Tecnici che potrai leggere in formato PDF per un anno. ABBONATI ORA, è semplice e sicuro.