Nulla si crea e nulla si distrugge; in effetti, per trasferire contenuti di tipo multimediale si fa riferimento a politiche di compressione al fine di ottimizzare l’enorme carico di lavoro richiesto dall’applicazione in gioco.
Audio e grafica: due campi abbastanza variegati con caratteristiche proprie ma che hanno un aspetto comune, ovvero l’esigenza di utilizzare sistemi di codifica che permettono di trasportare il contenuto informativo a prescindere dalla particolare applicazione in gioco. Sembra proprio una contraddizione, ovvero come si fa a restringere le informazioni senza per questo perdere nulla sul proprio contenuto informativo? Un’idea che, a prima vista, può sembrare azzardata ma che, poi, si è rivelata vincente. In effetti, per chi s occupa di trattamento dell’informazioni l’idea non è proprio azzardata: occorre solo trasformare la rappresentazione dei dati da un insieme di simboli ad un altro.
L’odierna tecnologia si basa su due interessanti schemi di compressione, ossia la codifica Huffman e la compressione LZW o Lempel and Ziv. Occorre precisare che Huffman e LZW sono tecniche di compressione definite di tipo "lossless", ossia nel processo di compressione non si perdono dati, che si contrappone a quelli di tipo lossy dove la compressione si verifica a fronte della perdita di dati “meno importanti”. Huffman e LZW sono due algoritmi lossless utilizzati in molte applicazioni e sono anche molto versatili tanto che il grado di compressione non è direttamente legato al contenuto dell’immagine ed essendo di tipo lossless, non c’è perdita di qualità. Di solito in campo grafico si utilizza il JPEG che appartiene all’insieme degli algoritmi lossy specializzato per le immagini e ha la particolarità di funzionare su immagini con molti sfumati (fotografie o paesaggi) e quando l’immagine ha un forte contrasto o passaggi bruschi di colore. È importante ricordare che gli algoritmi di compressione sono, al solito, raggruppati in due grandi famiglie: compressione statistica e compressione mediante sostituzione di testo o con dizionario. Nel primo caso ci troviamo nella situazione di dover prima esaminare il flusso da comprimere; in effetti, è necessario fare verifiche di tipo statistico sul formato dell’input per ottenere poi una buona compressione. Per esempio in un file di testo da comprimere si studia la frequenza relativa di ciascun carattere per associare poi al carattere presente più volte nel testo, il codice più corto, viceversa a caratteri presenti con frequenza bassa ci troviamo con una la parola più lunga. Di questo tipo di classe fanno parte codifiche come quella di Huffman. Al contrario, la compressione mediante sostituzione del testo si basa sull’idea di rimpiazzare, in un file, occorrenze di stringhe ripetute con puntatori a precedenti copie. In genere, la lunghezza di un puntatore è più piccola della lunghezza della stringa rimpiazzata. Da ciò risulta, che maggiori sono le ripetizioni di occorrenze di stringhe nel file da comprimere, maggiore è il grado di compressione raggiunta. Quindi, una delle attività dell’algoritmo di compressione è quella di trovare le stringhe che si ripetono. Questa particolare attività si svolge inserendo il file in un buffer di dati, chiamato dizionario. La velocità dell’algoritmo dipende poi dalla struttura dati utilizzata per implementare il dizionario, dall’algoritmo utilizzato per trovare i match tra le stringhe del file prese in considerazione e le stringhe presenti nel dizionario.
La compressione
Di solito ci si avvicina alla compressione utilizzando strumenti di tipo statistico sul segnale in ingresso. In effetti, sul flusso da trattare si ricorre a diversi passi: da una trasformazione lineare fino alla codifica entropica passando per la quantizzazione. Con la fase di trasformazione lineare il segnale in ingresso è decomposto nelle sue componenti di frequenza ricorrendo ad una trasformazione lineare. Questo particolare processo si preoccupa di decorrelare il segnale in modo che il valore di ogni coefficiente trasformato sia statisticamente indipendente dal valore degli altri coefficienti, oltre alla compressione dell’energia, in maniera tale che la maggior parte dell’energia del segnale si concentri in una piccola porzione dei coefficienti trasformati. Con la quantizzazione dai coefficienti del segnale si “tagliano” i bit meno significativi, in maniera uniforme o adattativa rispetto alla frequenza di ogni singola componente del segnale. La quantizzazione è il passo fondamentale nella compressione lossy: è un passo che consente di eliminare le informazioni meno importanti al fine di ottenere una maggiore compressione. Per questo motivo, nella compressione lossless, questo passo è omesso. Infine, per la codifica entropica i coefficienti quantizzati sono codificati in base a proprietà statistiche del segnale, secondo un modello noto a priori o in base a informazioni raccolte durante una fase di pre-processing, in modo tale da ridurre la ridondanza nella rappresentazione del segnale. Con la codifica Entropica si ricorre, quando è necessario, al controllo del fattore di compressione. In effetti, si ricorre a questa particolarità solo quando la dimensione dei dati compressi è fissata a priori, indipendentemente del processo di codifica. Di certo, insieme alla grafica, uno dei campi di maggiore importanza nel signal processing è la compressione audio anche per via dei recenti progressi tecnologici. In effetti, comprimere un segnale audio permette di minimizzare la quantità di risorse necessarie per la codifica, aumentando così le velocità di trasmissione dell’informazione e riducendo i costi e l’utilizzo di banda. Da un punto di vista tecnico, la compressione audio deve trovare il giusto compromesso tra il bitrate, il processing delay e la qualità del segnale. La qualità del segnale è di solito ricavata attraverso opportuni test soggettivi, ITU-R BS.1116 e BS.1254, oppure oggettivi, ITU-R BS.1387. Tra le varie tipologie di segnali audio, quelli di maggiore interesse nell’ambito della compressione audio sono quelli vocali e quelli musicali. Nel campo del segnale musicale si prende come riferimento il Compact Disk con codifica stereo, ossia due canali, con una frequenza di campionamento di 44.1 KHz e quantizzazione a 16 bit (1.4 Mbit/s). Viceversa, in ambito vocale il sistema di riferimento è il segnale telefonico di tipo digitale con una frequenza di campionamento di 8 KHz con quantizzazione a 8 bit (128 Kbit/s).
Gli algoritmi lossless
Rientrano in questa particolare categoria l’algoritmo di Huffman, LZ, LZ77, LZSS, LZ78 e LZW. La famiglia degli algoritmi di LZ, sebbene ha molte varianti, è basata essenzialmente sulla sostituzione di testo. Questa particolare famiglia ha il vantaggio di comprimere in modo semplice ed efficiente tipi di dati eterogenei, come testo, immagini o database. La caratteristica principale della famiglia LZ è che non richiede informazioni a priori sui dati, inoltre le statistiche sul file da comprimere sono acquisite implicitamente durante la fase di codifica. Il primo algoritmo di compressione di Lempel-Ziv è identificato come LZ77, ovvero Lempel-Ziv 77. In questo algoritmo il dizionario è creato a partire dalla sequenza precedentemente codificata. Per ottenere la codifica si esamina la sequenza in input tramite una finestra divisa in due parti. Una prima è una search buffer che contiene una parte della sequenza recentemente codificata, mentre l’altra window è una look-ahead buffer che contiene la prossima porzione della sequenza che deve essere codificata. L’algoritmo cerca, ad ogni passo nella sequenza di caratteri, una sottostringa che è già stata incontrata e se tale sequenza esiste è compressa mediante un puntatore alla precedente occorrenza. In questo modo, più il file contiene elementi ripetuti, più la compressione è efficace. In un file di testo, ad esempio, se si incontra una ripetizione di una parola, la seconda viene sostituita con l’indirizzo della prima. L’algoritmo LZSS, formulato da James Storer e Thomas Szymanski nel 1982, intende eliminare alcune incongruenze dell’algoritmo LZ77. In effetti, in base a diverse verifiche, l’algoritmo LZ77, nel caso in cui non vengono trovati match nella window, ritorna in output un carattere dopo ogni puntatore. Questa particolare gestione implica, in modo intrinseco, una certa ridondanza: ossia o sarà ridondante il puntatore nullo o il carattere che potrebbe essere incluso nel prossimo match. A questo proposito, l’algoritmo LZSS risolve questo problema in modo più efficiente: il puntatore è restituito solo se punta a un match più lungo del puntatore stesso, altrimenti saranno restituiti dei caratteri. Per questa ragione, siccome lo stream di uscita della compressione sarà costituito da caratteri e puntatori, sarà necessario ad ognuno un bit supplementare che ci permetterà di distinguere le tipologie. L’algoritmo LZ78 venne sviluppato a partire da LZ77 per eliminarne i problemi incontrati fino ad allora. In effetti, con la versione LZ77 il dizionario era definito da una window di lunghezza fissa riferita al testo precedentemente analizzato, con la variante LZ78 si è deciso di non utilizzare più, il concetto di windows. Non solo, in questa particolare variazione il dizionario diventa ora una collezione potenzialmente illimitata di frasi precedentemente analizzate: si inserisce le frasi in un dizionario e, quando viene trovata un occorrenza ripetuta, è restituito un token, ovvero un indice del dizionario al posto della frase stessa, e il carattere che segue la frase. Rispetto alla variante LZ77 in questa soluzione non c’è più necessità di passare la lunghezza della frase come parametro alla funzione di compressione perché risulta già conosciuta. Nell’algoritmo LZW sono restituiti, nella fase di codifica, solo i codici delle parole. Questo significa che il dizionario non può essere vuoto all’inizio di questa fase, ma dovrà contenere tutte le stringhe di un solo carattere dei dati in input. Poiché tutte le stringhe di un solo carattere sono già nel dizionario, ogni passo di codifica inizia con un prefisso di un carattere. Per questa ragione la prima stringa cercata nel dizionario disporrà di due caratteri: il carattere con il quale inizia il nuovo prefisso e l’ultimo carattere della precedente stringa. Questa scelta deriva dalla necessità di permettere all’algoritmo di decodifica di ricostruire il dizionario senza l’aiuto di caratteri espliciti nella sequenza codificata. Riassumendo, la codifica di Huffman, proposta nei primi anni ‘50, riduce il numero di bit usati per rappresentare caratteri frequenti ed aumenta quello dei caratteri non frequenti. La tecnica LZW, invece, usa i dati immessi per costruire un alfabeto espanso, basato sulle stringhe incontrate. Questi due differenti approcci lavorano entrambi riducendo le informazioni ridondanti nell’immissione delle informazioni.
Algoritmo di Huffman
Come si è giù più volte ribadito, il principio su cui si basa la compressione dei dati è l’eliminazione della ridondanza contenuta nell’informazione. L’obiettivo è rappresentare un segnale utilizzando il minor numero possibile di simboli, in accordo a determinati vincoli di qualità sul segnale ricostruito. L’algoritmo di Huffman analizza le frequenze dei simboli da comprimere, sostituendo un codice, tipicamente ad 8 bit, con una sequenza più corta di bit (minimo 1), in funzione della frequenza del dato da comprimere e alla base dell’algoritmo di Huffman c’è sempre un indagine di tipo statistico. L’algoritmo si basa su diversi passi. Per prima è necessario esaminare i dati da comprimere per verificare la frequenza dei vari caratteri e solo successivamente si crea un codice ottimo con un raggruppamento di simboli in ordine di occorrenza e si combinano i due simboli con occorrenza minore, creando un nuovo nodo (che avrà occorrenza pari alla somma delle occorrenze dei due) e mettendoli come figli. Il processo si ripete fino a quando non si ottiene un albero. Al termine è necessario sostituire le stringhe di bit che rappresentano i caratteri con i corrispettivi e si aggiunge come intestazione il codice calcolato. Il codice che si crea viene detto pre-fisso in quanto nessuna delle stringhe di bit risulta essere prefisso di un’altra (ad esempio 11 non è prefisso di 1001), in questo modo non è necessario inserire dei marcatori tra un codice e l’altro. La figura 1 mostra una rappresentazione grafica della compressione della stringa “CIAO_AMICI”.
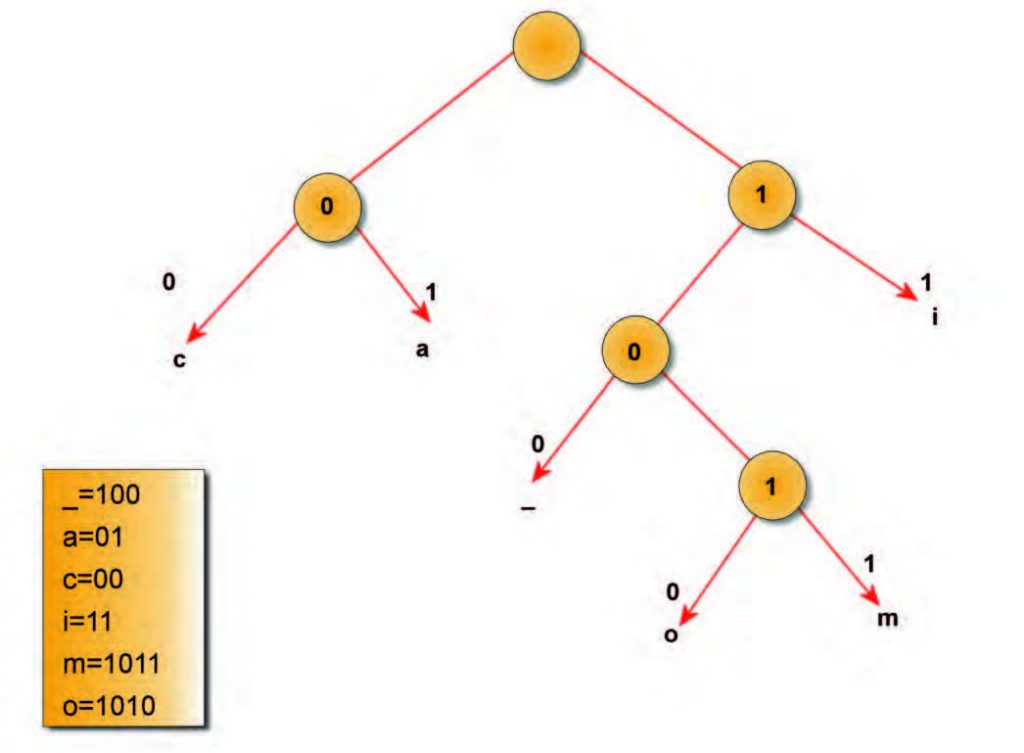
Figura 1: ciao amici.
Ogni lettera è rappresentata da 8 bits codificati rispettando la codifica Ascii e, per questo, le lettere dell'esempio saranno quindi codificate nel modo seguente:
A = 01000001
C = 01000011
I = 01001001
O = 01001111
M = 01001101
_ = 00100000
Il messaggio è quindi costituito da una stringa di 80 bit, 10 lettere per 8 bit, come:
01000011 01001001 01000001 01001111
00100000 01000001 01001101
01001001 01000011 01001001.
Una volta compressa la stringa si ottiene un messaggio pari a 0011011010100011011110011, lunghezza 25 bits, con un rapporto di compressione del 68,75%. La codifica Huffman è impiegata nei codec MPEG Layer-3 per comprimere ulteriormente la sequenza numerica ottenuta dopo la quantizzazione non lineare. Se volessimo codificare la stringa di valori digitali in figura 2, per prima cosa dobbiamo analizzare la frequenza delle parole ed associamo loro il corrispondente codice Huffman, tabella 1, ottenendo così la corrispondente sequenza codificata in Huffman in figura 3.

Tabella 1: corrispondente codice Huffman.

Figura 2: bit stream.

Figura 3: risultato finale.




