
I robot sono tra noi e questa è la realtà già da un pò di tempo a questa parte. Tuttavia, per chi è cresciuto con Terminator, i robot che sono tra noi sono un pò deludenti. A parte per il non essere alti e palestrati, non si muovono molto bene e non sono neanche particolarmente svegli. Ma perché? Del resto, vengono equipaggiati con CPU allo stato dell’arte e possono essere dotati di tutti i migliori sensori in circolazione. Tutto verissimo, ma vedere in Full-HD non significa riuscire anche a capire che cosa si sta guardando. Mettiamo dentro una rete neurale, vanno molto di moda al giorno d’oggi. Bene. Ma di nuovo, perché? Una rete neurale è un circuito che estrae da ciò che gli viene dato in ingresso una serie di caratteristiche, di features nell’inglese che fa tanto figo, e le confronta con quelle che ha estratto in passato da altri input che ha esaminato. A seconda di cosa estrae e di come lo fa, la rete neurale può essere in grado o meno di estrarre informazioni da ciò che esamina. E questo, in effetti, è ciò che facciamo anche noi quotidianamente, senza neanche rendercene conto. Siamo in grado di riconoscere un televisore indipendentemente da marca e modello perché si tratta di un oggetto rettangolare, piatto, con un basamento e con un’immagine che si muove sullo schermo. “Rettangolare”, “piatto”, “presenza di basamento” e via dicendo sono features. E oggi vi parleremo dello strumento alla base di qualsiasi estrazione di features: il filtro.
POTENZA DEI FILTRAGGI
Sì, lo so cosa state pensando. Sappiamo cosa sono i filtri. Ce ne hanno riempito la testa all’università. Prendi un segnale, tipo un segnale musicale, o uno vocale, gli fai la trasformata di Fourier, e poi lo moltiplichi punto a punto per un’altra funzione più o meno rettangolare (Figura 1).
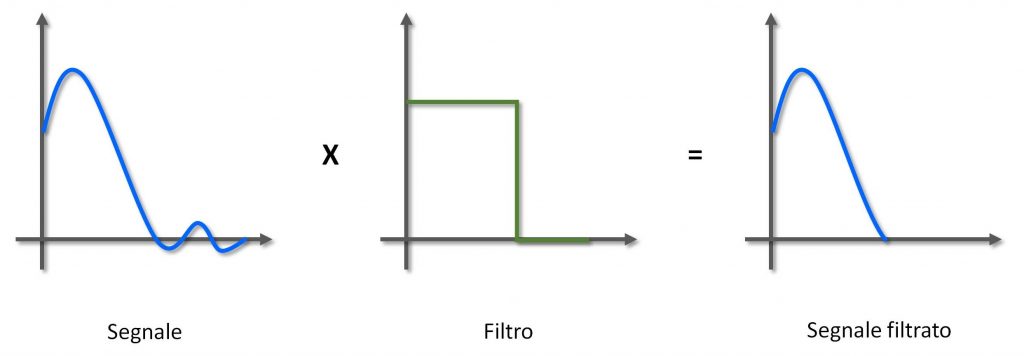
Figura 1: Filtraggio nel dominio della frequenza
Così facendo, possiamo per esempio togliere magicamente del rumore, oppure… boh… equalizzare? Sì, qualcosa del genere. Nulla di troppo entusiasmante in ogni caso. Posso condividere la scarsa eccitazione. E del resto, usciamo dal seminato: che se ne fa un robot di un filtro di denoising? Sì, migliora la qualità dell’audio, ma tutto lì. Cambiamo settore, allora. Domanda: possiamo fare la stessa cosa per un’immagine? Per chi si sta grattando perplesso la testa, un indizio: Photoshop ha una bella collezione di filtri. Quindi sì, un’immagine si può filtrare. Perché la si possa filtrare ce lo dice Photoshop stesso: per applicare tutta una serie di effetti molto carini. Ma perché questo possa essere utile nel nostro contesto non è tanto ovvio.
Per capire, invece, perché il filtraggio delle immagini sia qualcosa di fondamentale per la loro interpretazione, torniamo al denoising. Quando ci mostrano schemi come quelli nella Figura 1, lo fanno perché è più semplice. Sono due funzioni che moltiplichi punto a punto. Spesso, però, così facendo, si perde il senso di che cosa questo significhi. Ogni punto del grafico a sinistra nella Figura 1 rappresenta l’ampiezza di una componente ad una certa frequenza del segnale originale; è l’ampiezza di una sinusoide a quella particolare frequenza che “vive” nel segnale originale. Se quella componente la abbattiamo, eliminiamo quella sinusoide dal segnale originale.
Noi però viviamo nel dominio del tempo, non in quello della frequenza; noi sentiamo una canzone, non delle sinusoidi. Quindi, qual è l’effetto dell’eliminazione di quella sinusoide nel dominio del tempo? Eliminiamo una variazione paragonabile con quella sinusoide!
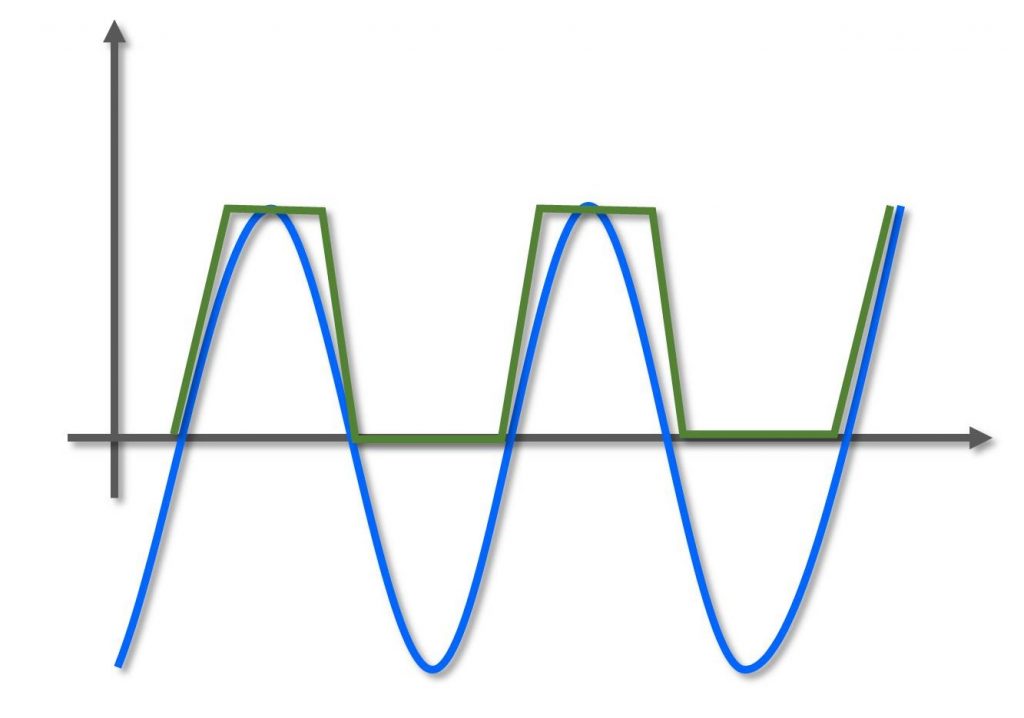
Figura 2: Approssimazione di un segnale con una sinusoide
Osservate la Figura 2. La trasformata di Fourier ci dice che il segnale originale lo possiamo scrivere come somma di tutte quelle sinusoidi che essa stessa estrae. Queste sinusoidi, provenendo dal nostro segnale, non possono essere qualsiasi: devono necessariamente richiamare qualche sua caratteristica. E in più, inevitabilmente, non ci basterà una sinusoide per approssimare correttamente il segnale, ma a seconda di come è fatto ce ne vorrà un numero più o meno grande. Ecco quindi che un segnale che varia rapidamente (ad esempio un’onda quadra con dei fronti molto ripidi) conterrà delle sinusoidi molto “veloci”, ossia a frequenza elevata; un segnale che varia lentamente, invece, conterrà principalmente sinusoidi “lente”, ossia a bassa frequenza. Ecco perché si dice che un segnale con fronti molto ripidi occupa una banda elevata: perché nel dominio della frequenza avrà componenti a frequenza molto alta. Ed ecco perché se eliminiamo queste frequenze il segnale perderà le sue variazioni rapide e finirà per “addolcirsi”.
Tutto questo è abbastanza semplice da spiegare se si ragiona nel dominio della frequenza; molto meno se si ragiona in quello del tempo. Come recita la filastrocca imparata a scuola, “la moltiplicazione in frequenza corrisponde alla convoluzione nel tempo, e viceversa”. Dunque, lo stesso risultato si può ottenere in due modi diversi, di cui il secondo in genere viene ignorato in quanto la convoluzione è un integrale, che, a seconda dei casi, può essere anche molto brutto e cattivo.

Figura 3: FFT di un'immagine
Questo, nel caso del filtraggio delle immagini, è un pò un problema. Si può fare la trasformata di Fourier di un’immagine? Sì, senza eccessivi problemi. L’integrale diventa doppio e un pò di cose al suo interno vanno generalizzate, ma non è impossibile. Che informazioni mi dà lo spettro? Questa è più difficile. La Figura 3 mostra lo spettro di un’immagine. Che vi dice? Non molto, in effetti. C’è parecchio contenuto in bassa frequenza, indubbiamente, e un pò di roba verticale e orizzontale (le righe sugli assi cartesiani della figura, che rappresentano sinusoidi disposte orizzontalmente e verticalmente). In questo caso, applicare un filtro passa-alto significa eliminare il “centro” della trasformata di Fourier, e l’effetto è quello mostrato nella terza immagine: si esaltano i bordi della figura. Applicare un filtro passa-basso significa, invece, eliminare tutto tranne il centro della trasformata, e così facendo si eliminano i bordi della figura, ottenendo un’immagine sfocata come nella quinta immagine. Ma andare oltre questi semplici esempi è abbastanza difficile. Purtroppo, quando si tratta di filtraggio di immagini, bisogna rassegnarsi: si deve usare la convoluzione.
QUESTA BISTRATTATA CONVOLUZIONE
Fortuna vuole che le immagini abbiano una particolarità: sono segnali discreti. Un’immagine non ha infiniti punti colorati, è fatta di pixel; di punti ce ne sono solo un pò. Quindi? Quindi questo significa niente integrale! Non ha senso usare un integrale, che è un oggetto che lavora su quantità infinitesime, su un qualcosa che quantità infinitesime non ne ha. E se ricordate che un integrale queste quantità infinitesime le somma, non vi stupirete se vi dico che la convoluzione per segnali discreti è questa qui:
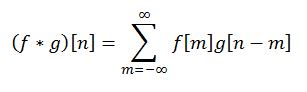
Ok, questa è la formula. Ma dal punto di vista operativo, che ci dice? Come si fa questa convoluzione? Allora, qui f è il segnale di partenza, g la risposta impulsiva del filtro (ossia come il filtro è fatto), n identifica un certo campione del segnale (come fosse l’indice i in un ciclo for quando si scorre un array) e m è un altro indice, che qui rappresenta il punto cruciale. La formula ci dice che, per calcolare un certo campione in uscita, dobbiamo esaminare tutti i campioni del segnale in ingresso (da meno infinito a più infinito), e moltiplicarli punto a punto per la risposta impulsiva del filtro rovesciata.
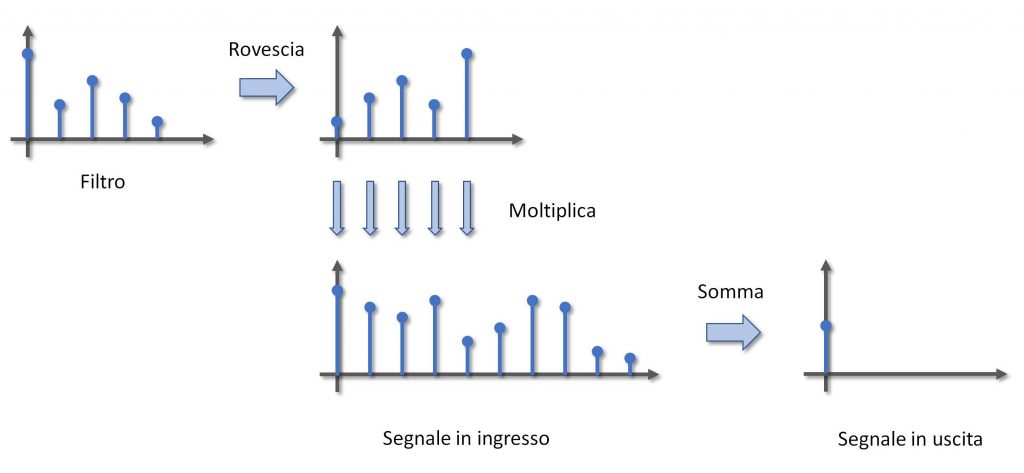
Figura 4: Calcolo della convoluzione in 1D
Sì, non è molto chiaro. Innanzitutto, perché il filtro è rovesciato? Bè, basta fare un esempio. Supponiamo che sia n = 0. Il segnale viene moltiplicato per g[-m]. Questo significa che f[1] viene moltiplicato per g[-1], f[2] per g[-2] e così via. È lo stesso che prendere f[1] e moltiplicarlo per g[1] dopo aver rovesciato g, come si vede nella Figura 4. Operativamente, rovesciare g e poi fare le moltiplicazioni è più comodo. Al giro successivo, poi, si sposta g avanti di una posizione e si ripete il procedimento. Una convoluzione a tempo discreto è tutta qui: rovesci g, moltiplichi e sommi; poi trasli di uno, moltiplichi e sommi, e così via all’infinito, o fino a che f non finisce. [...]
ATTENZIONE: quello che hai appena letto è solo un estratto, l'Articolo Tecnico completo è composto da ben 2678 parole ed è riservato agli ABBONATI. Con l'Abbonamento avrai anche accesso a tutti gli altri Articoli Tecnici che potrai leggere in formato PDF per un anno. ABBONATI ORA, è semplice e sicuro.







