
Cosa significa “riconoscere un oggetto”? Intuitivamente, significa separarlo da tutto il resto, significa poter dire “questa è una mela” e “questo è un tavolo”. Significa riconoscere il punto in cui finisce la mela e in cui inizia il tavolo. E se prendessimo una foto di una mela su un tavolo, cosa ci sarebbe sull’immagine a separare i due? Ciò che comunemente chiamiamo “bordo” o edge, nell’inglese che tanto la fa da padrone in questo campo. Per riconoscere un oggetto, è fondamentale essere in grado di distinguere i suoi bordi. Per un uomo è in genere piuttosto semplice, per una macchina molto meno. È questo uno dei motivi fondamentali per cui c’è tanto interesse attorno agli algoritmi in grado di estrarre i bordi di un’immagine, ed è di uno di questi di cui vi parleremo oggi.
POTENZA DEI FILTRAGGI - RELOADED

Figura 1: Mele su un tavolo
Osservando la Figura 1, da cosa capiamo dove finisce la mela e inizia il tavolo o, in generale, dove si trova un bordo? Normalmente, perché là dove c’è un bordo di solito c’è una variazione di colore; ad esempio, si passa dal rosso della mela al marrone grigiastro del legno del tavolo. Oppure, ci potrebbe essere una sottile linea nera, che sempre una variazione di colore è. “Variazione” qui è la parola cruciale. Un bordo coincide sempre con una variazione di colore o luminosità. Questo è fondamentale, perché sappiamo dai cari tempi del liceo come fare per trovare le variazioni in un segnale: si calcola la derivata.

Figura 2: Mele filtrate
Abbiamo visto la scorsa volta come si possano estrarre i bordi di un’immagine: basta applicare un opportuno filtraggio. Di filtri adatti ce ne sono tanti; uno è quello di Sobel, il risultato della cui applicazione è riportato nella Figura 2, ma più o meno tutti estraggono la stessa roba. C’è però un però. Come si vede dalla Figura 2, il filtro non estrae solo i bordi che ci interessano, ma anche un sacco di altra roba che dà più fastidio che altro. Come tutti gli oggetti che estraggono le variazioni di un segnale, i filtri per l’estrazione dei bordi sono molto sensibili al rumore. Si tratta, fondamentalmente, di filtri passa-alto, che eliminano la parte più costante del segnale (dunque le zone uniformi dell’immagine) e ne mantengono quella che varia, dunque bordi e, inevitabilmente, rumore. Per questo motivo, è buona norma far precedere questo filtro da un filtro Gaussiano che, sfocando un pò l’immagine, a tutti gli effetti rimuove tutte quelle variazioni piccole e trascurabili che poco aggiungono alla comprensione dell’immagine.

Figura 3: Filtraggio con un kernel Gaussiano 5x5
I filtri gaussiani possono essere presi grandi a piacere. Più è grande il filtro, maggiore è l’area di sfocatura, e quindi più rumore viene rimosso. Tuttavia, se il filtro è troppo grande, con il rumore potrebbero andarsene anche componenti dell’immagine che invece vorremmo mantenere, tipo bordi sottili o deboli. In genere un kernel 5x5 è più che adatto allo scopo, ma a seconda dei casi se ne potrebbe preferire uno più grande.
Ora, un filtro gaussiano più grande ha un altro svantaggio: fa più conti, e quindi risulta essere più pesante per il processore, soprattutto se si considera che dopo questo filtraggio bisogna farne almeno altri due, uno per i bordi orizzontali e uno per quelli verticali. Una cosa intelligente che possiamo fare, quindi, è combinare i due filtraggi: considerato che andremo a calcolare la derivata dell’immagine filtrata, non è che per caso otterremmo lo stesso risultato filtrando l’immagine con la derivata del filtro? In effetti sì. Ma come si fa a calcolare la derivata di un filtro? Banalmente, filtrando il filtro (!) con un opportuno kernel! Per quanto sembri che ci stiamo riempiendo la bocca con uno scioglilingua, la faccenda non è tanto assurda, a pensarci un attimo. Un kernel gaussiano è una matrice, e una matrice la possiamo sempre vedere come un’immagine, dunque filtrare un filtro è perfettamente legittimo.

Figura 4: Estrazione dei bordi
E come si vede dalla Figura 4, la faccenda funziona. Qui abbiamo estratto sia i bordi verticali che quelli orizzontali, in due immagini separate. Molto bello, però, due immagini sono forse un pò troppo. Voglio dire, il bordo alla fine deve essere uno, non ha senso guardare su un’immagine la parte orizzontale dei bordi e su un’altra quella verticale. Molto meglio sarebbe avere un’immagine soltanto con entrambi i bordi combinati in qualche modo.
In realtà, molto meglio è comunque avere due immagini, solo non queste qui. Ragioniamo un attimo. Chi è passato attraverso la Grande Tribolazione che è Analisi II, forse ricorderà il concetto di derivata direzionale. Sostanzialmente, quando si calcola la derivata di un qualcosa con più di una dimensione, non ricaviamo solo l’entità della variazione, ma anche la sua direzione, come è giusto che sia. In più di una dimensione, la derivata è un vettore, e le due immagini della Figura 4 ci danno, punto per punto, la sua componente orizzontale (x) e la sua componente verticale (y).
Sempre chi è passato per quella Grande Tribolazione di cui sopra, ricorderà forse che un vettore, oltre che esprimerlo con la sua larghezza e la sua altezza, lo possiamo esprimere anche in termini di sua lunghezza e di quanto è inclinato rispetto all’orizzontale: modulo e fase. Lo stesso possiamo fare qui. Se la derivata di un’immagine è punto per punto una grandezza vettoriale, punto per punto possiamo calcolare il suo modulo e la sua fase.

Figura 5: Modulo e fase dei bordi
Il risultato è mostrato nella Figura 5, in falsi colori; a sinistra il modulo e a destra la fase. Come si vede, il modulo contiene la gran parte delle informazioni sui bordi (notate come si vedano bene i contorni delle ombre o la fessura tra gli assi del tavolo), mentre la fase quelle relative alla loro orientazione. Tuttavia, a questo punto della faccenda non abbiamo ancora estratto un bel niente. I bordi non sono uniformi; alcuni sono spessi, mentre ci aspetteremmo qualcosa di più sottile. Altri invece cambiano di intensità strada facendo, mentre ci aspetteremmo che i pixel sul bordo avessero tutti lo stesso valore. Il resto dell’algoritmo serve proprio per sistemare questi problemi.
PER QUALCHE ELABORAZIONE IN PIU'
“Assottigliare” un bordo concettualmente non è difficile: per ogni “sezione” del bordo, prendiamo un pixel soltanto. Quale? Il massimo sembra la scelta più opportuna. Il punto semmai è quale massimo. Osservando la Figura 5, sembrerebbe (e in effetti è così) che di pixel massimi ce ne possano essere più di uno, ad esempio sopra, a destra e in alto a destra rispetto al pixel corrente. Del resto, se il bordo è un pò grosso non stupisce poi tanto che di pixel di valore elevato ce ne siano un pò tutti insieme.
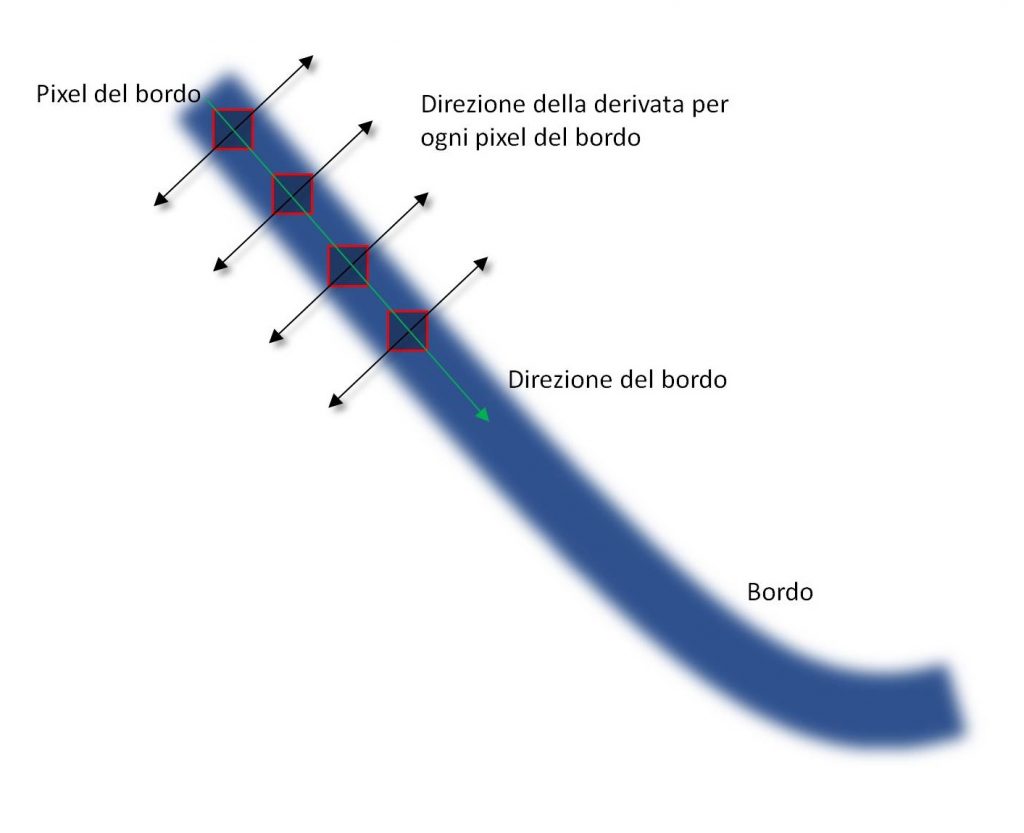
Figura 6: Direzione del bordo e della derivata
Quale scegliere ce lo dice la direzione del bordo, e questa direzione viene direttamente da quella della derivata che abbiamo calcolato, quella nella seconda immagine della Figura 5. Il bordo sarà perpendicolare alla derivata, come nella Figura 6; questo ha un senso, dato che, per esempio, variazioni orizzontali identificano bordi verticali e viceversa. Dunque, se consideriamo i pixel lungo la direzione della derivata, sarà come se stessimo vedendo cosa succede ai lati di un bordo, fuori da esso. Il massimo pixel per quella sezione di bordo sarà il pixel massimo lungo la derivata.
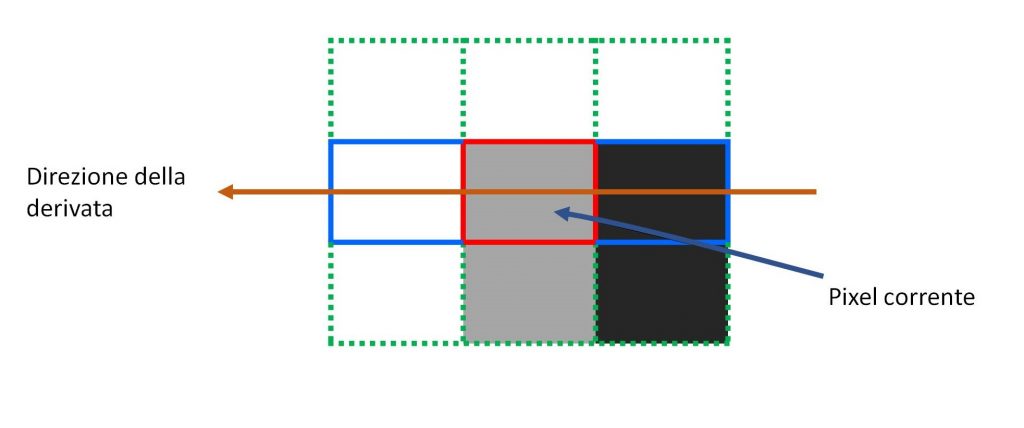
Figura 7: Esempio di non maximum suppression
ATTENZIONE: quello che hai appena letto è solo un estratto, l'Articolo Tecnico completo è composto da ben 2318 parole ed è riservato agli ABBONATI. Con l'Abbonamento avrai anche accesso a tutti gli altri Articoli Tecnici che potrai leggere in formato PDF per un anno. ABBONATI ORA, è semplice e sicuro.








Complimenti per l’esposizione chiara e comprensibile di un argomento, molto interessante, e sicuramente non facile come la visione artificiale.
Denota una notevole padronanza della materia .