Quando si parla di “riconoscere” un oggetto in un’immagine o un video, in genere la prima cosa che viene in mente sono quei filmati di youtube in cui una qualche intelligenza artificiale piazza un rettangolino colorato attorno ad una persona, o ad una macchina, o a quello che vi pare. Questa “definizione”, se così la vogliamo chiamare, riflette l’associazione (limitativa) che spesso si fa tra Computer Vision e reti neurali: per molti, la prima è in funzione della seconda, esiste solo perché poi va usata da una rete neurale. Le reti neurali vanno piuttosto di moda, oggigiorno, e capita spesso che, quando c’è un problema da risolvere, la prima cosa che si pensa di fare è buttarne dentro una. Ma le cose non funzionano così. È vero il contrario: è il mondo della Computer Vision ad essere più ampio. In questo mondo, esistono diverse declinazioni del verbo “riconoscere”, e oggi ve ne mostreremo alcune.

METTERCI LA FACCIA

Figura 1: Riconoscimento di un volto

Ok, abbiamo un’immagine con un qualcosa che ci interessa dentro, e sappiamo come estrarne le features. Cosa ce ne facciamo? La cosa più ovvia è il matching: in pratica, andiamo a cercare quelle stesse features in un’altra immagine. Perché? Bè, le applicazioni possibili sono parecchie. Per esempio, pensate a quando nei film usano dei software automatici per identificare il volto dei cattivi nei video delle telecamere di sorveglianza: questo è un caso di features matching. Se si estraggono le features dal volto, e si ritrovano quelle stesse features nel video, abbiamo trovato il nostro cattivo!

Per inciso, potete capire a questo punto come mai si tratti di una cosa diversa dal riconoscimento dei volti tramite rete neurale. In questo caso utilizziamo delle features estratte da una immagine per riconoscere un particolare volto in una serie di immagini; nel caso delle reti neurali, si estraggono delle features per così dire “generiche” che permettono alla rete di estrarre qualsiasi volto dalla serie di immagini. Il riconoscimento di una particolare cosa o persona è possibile con una rete neurale solo se si dispone di un numero sufficiente di immagini di quella cosa o persona da addestrare la rete; e non è detto che sia sempre così.

Possiamo farlo con un certo grado di accuratezza? Dipende. Dipende da che tipo di features stiamo usando per il matching. L’accuratezza nel matching è il motivo fondamentale per cui abbiamo speso tutte quelle parole, la scorsa volta, sull’importanza di avere features invarianti per rotazioni e scalatura. In questo modo, possiamo riconoscere il volto del cattivo anche se è più piccolo di quello nella foto segnaletica e in un’altra posizione. Come possiamo farlo? Confrontando i descrittori che abbiamo estratto insieme alla feature. Li abbiamo ricavati apposta. Se due features hanno descrittori simili (perché uguali non saranno mai), è molto probabile che si tratti della stessa cosa.

Ora, analizziamo questa frase. “Se due features hanno descrittori simili” è un’affermazione che implica che disponiamo di un qualche modo per decidere se due features sono simili oppure no. In genere, in questo campo (e in molti altri), quando si vuole sapere se due cose sono simili oppure no, ciò che si fa è calcolare la relativa distanza. In matematica, il concetto di “distanza” è (come al solito) più generale di quello a cui sono abituati i comuni mortali. Per noialtri, la distanza è "quanto spazio c’è da qui a lì"; per un matematico è un numero prodotto da una funzione che lavora su due input, “qui” e “là”. Il come venga calcolato questo numero è totalmente indifferente, basta che rispetti un certo numero di proprietà piuttosto ovvie per una cosa che vogliamo classificare come “distanza”. Dunque, molte delle “distanze” che spesso vengono usate in questi contesti sono definite, per così dire, “a senso”.

Prendiamo un descrittore del SIFT. Abbiamo visto l’altra volta che si tratta di un vettore fatto da 128 numeri. Per calcolare la distanza tra due di questi potremmo, ad esempio, calcolare la differenza in valore assoluto tra i termini relativi:

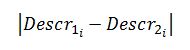
dove la i indica l’i-esimo elemento del descrittore. Così però ci troviamo ad avere tra le mani 128 differenze: che ce ne facciamo? Potremmo, ad esempio, sommarle:

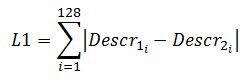
Così facendo, otterremo un numero che è tanto più grande quante più differenze significative ci sono tra i vari elementi dei descrittori. Sostanzialmente, otterremo un numero che è tanto più grande quanto più diversi sono i due descrittori, che è proprio ciò che volevamo.

In alternativa, invece che sommare i valori assoluti, potremmo sommare le differenze al quadrato:

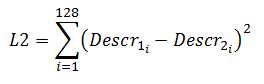
Funziona lo stesso, e in maniera analoga di distanze se ne possono definire molte altre.

Calcolata la distanza, possiamo scegliere come matching quella feature a distanza minima dalla nostra. Tuttavia, questo non ci mette al riparo da un problema: e se il nostro cattivo si fosse messo un cappello, coprendo magari mezza faccia con l’ombra? Ci ritroveremmo con parecchie features che non hanno un match o, peggio, che l’algoritmo matcha (abusatissimo inglesismo, si pronuncia meccia, da “to match”) erroneamente con un’altra che in realtà sarebbe molto distante.

Potremmo pensare di mettere una soglia: se la distanza calcolata è maggiore della soglia, non lo si considera un match. Se non ci sono distanze sotto soglia, si considera la feature senza match. Tuttavia, lavorare con una soglia è pericoloso, perché le prestazioni dell’algoritmo potrebbero dipendere fortemente dal valore della soglia o, peggio ancora, potrebbe darsi che per un algoritmo differente sia necessario un valore completamente diverso di soglia. In genere il valore “ottimo” della soglia lo si sceglie a valle di un numero (preferibilmente cospicuo) di test, prendendo il valore che, nella maggior parte dei casi, mantiene basso il numero di falsi match. Quindi, se per qualche motivo si decidesse di cambiare l’algoritmo di estrazione delle features, è probabile che si debbano rifare daccapo tutti i test, per scegliere la nuova soglia, e questa è una cosa che nessuno ha voglia di fare.

Una soluzione più ingegnosa consiste nel calcolare il rapporto tra la distanza minima trovata (quella del “best match”) e quella immediatamente dopo (il “second best match”). A questo test viene dato il nome poco fantasioso di ratio test. Se questo rapporto è basso, si tiene il match, altrimenti no. In effetti, se il rapporto è basso, significa che il second best match è molto diverso dal best match, e dunque che molto probabilmente il second best match è un falso positivo. Al contrario, se il rapporto è alto, significa che i due match sono all’incirca uguali, e quindi che molto probabilmente non sono buoni nessuno dei due: non ci possono essere due best match uguali! In più, il test non è influenzato dalla scelta dell’algoritmo.

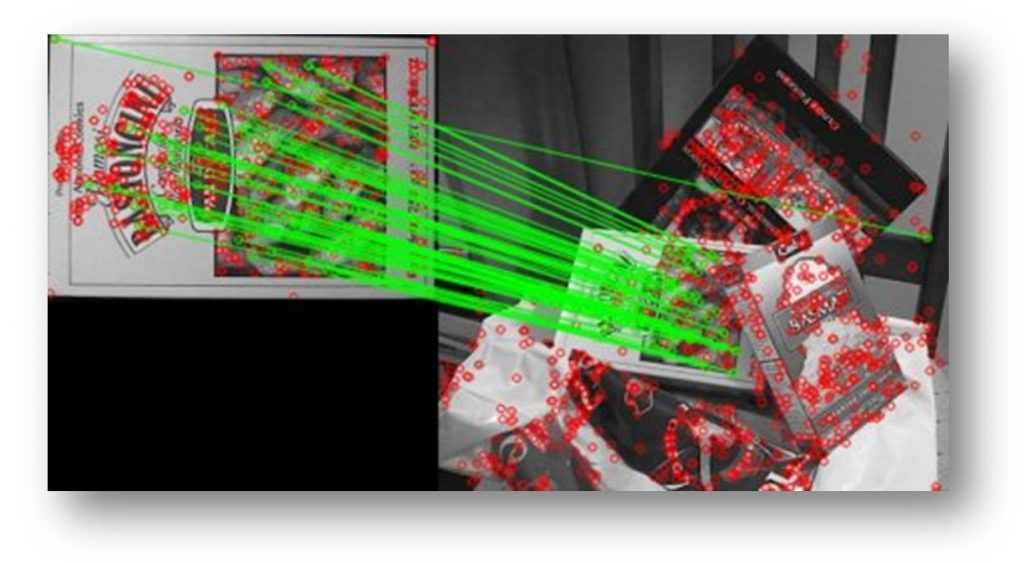
Figura 2: Riduzione dei match con il ratio test

La Figura 2 mostra la riduzione dei match con il ratio test. In verde le linee che collegano due features che l’algoritmo ritiene matchare (“mecciare”), in rosso tutte le altre features. Notare il match palesemente sbagliato dall’angolo in alto a sinistra (anche se l’algoritmo potremmo anche perdonarlo, visto che comunque ha trovato due angoli bianchi con fondo nero!).

Da questa figura dovrebbe essere anche evidente uno dei problemi principali dell’algoritmo di matching: ci sono un sacco di match da verificare! In genere un algoritmo di estrazione delle features estrarrà molte features, e queste vanno provate tutte. Ci sono diversi modi per farlo. Il più ovvio e semplice è quello a forza bruta: si prende una feature e se ne calcola la distanza con tutte le altre. Sicuramente troveremo il best match, ma potrebbe volerci un pò di tempo. Per ridurre un pò i tempi di elaborazione, OpenCV nel suo metodo per l’estrazione delle features consente di aggiungere un parametro che limita il numero di features estratte ad un massimo. In alternativa, esistono approcci un pò più ingegnosi. Uno uscito da un paio d’anni è il FLANN. Si tratta di un algoritmo che organizza le features in una particolare struttura ad albero per razionalizzare un pò la ricerca. E nessuno si sorprenderà nell’apprendere che OpenCV ha anche questa al suo interno. La fregatura è la “A” in FLANN. Quella “A” sta per “Approximate”; dunque, l’algoritmo ricaverà sì un best match, e più rapidamente dell’approccio a forza bruta, ma non è detto che sia il migliore in assoluto. La vita dell’ingegnere, si sa, è una coperta corta.

RIMETTERSI IN LINEA

Facciamo adesso non un passo indietro, ma semmai di lato. Considerate quest’altro esempio: stiamo cercando di fare una foto con il cellulare ad un documento e, come al solito, è venuta tutta storta. Possiamo in qualche modo raddrizzarla? Bè, considerato che ci sono app che già lo fanno in automatico, evidentemente la risposta deve essere sì, ma come?

A voler essere rigorosi, la risposta la dovremmo andare a cercare nel reame dell’algebra lineare e degli spazi vettoriali. L’algebra lineare è una di quelle branche della matematica così tremendamente astratte da risultare, nei suoi formalismi, probabilmente una delle cose più noiose mai concepite da mente umana… almeno fino a quando non ci si comincia a rendere conto che le sue applicazioni sono, letteralmente, ovunque.

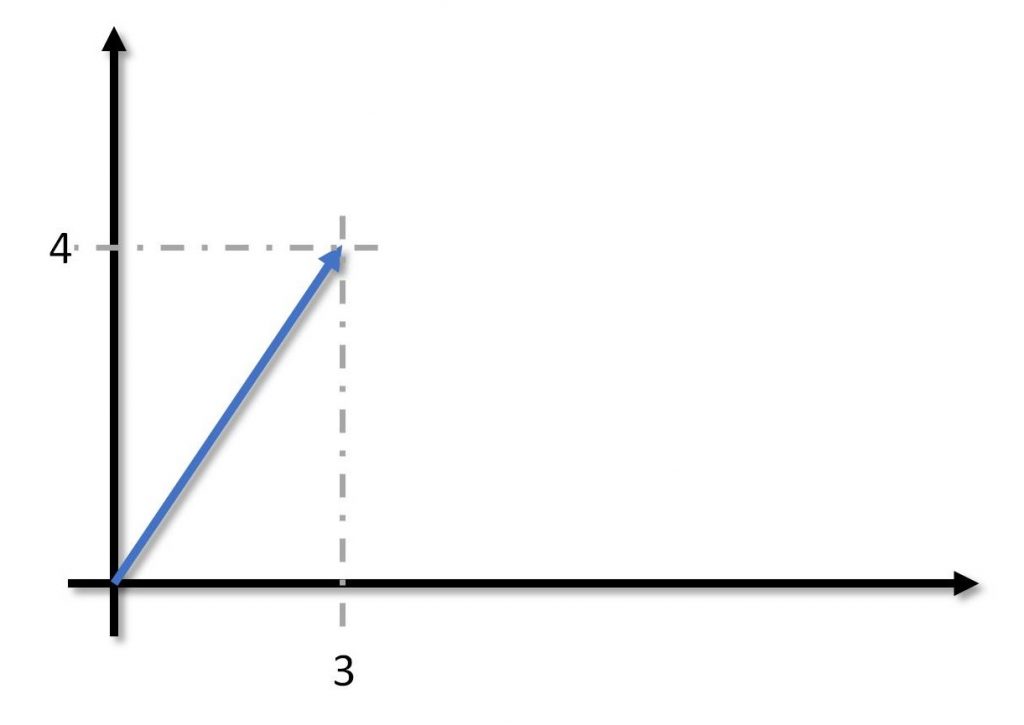
Figura 3: Un semplice spazio vettoriale

Per i nostri scopi, qui, serve giusto ripassare un paio di cose. Prendiamo un’immagine. Un’immagine è uno spazio vettoriale. Il motivo è che, se decidiamo (arbitrariamente) che un suo punto è l’origine, possiamo identificare univocamente ogni suo altro punto con un vettore, che potete visualizzare come la freccetta nel piano cartesiano (Figura 3).

Ok. Le cose si fanno interessanti quando a questi vettori si vuole applicare qualche trasformazione. L’algebra lineare chiama queste trasformazioni “applicazioni lineari”, che è un modo per dire che stai facendo qualcosa sul vettore (“applicazione”) e che lo stai facendo non in modo qualsiasi, ma rispettando certe regole (“lineari”). Dal punto di vista operativo, mediante tutto un giro di lemmi e teoremi, si possono codificare queste trasformazioni sotto forma di matrici. Le matrici rendono calcolabile in maniera semplice l’effetto di qualsiasi trasformazione vi possa venire in mente.

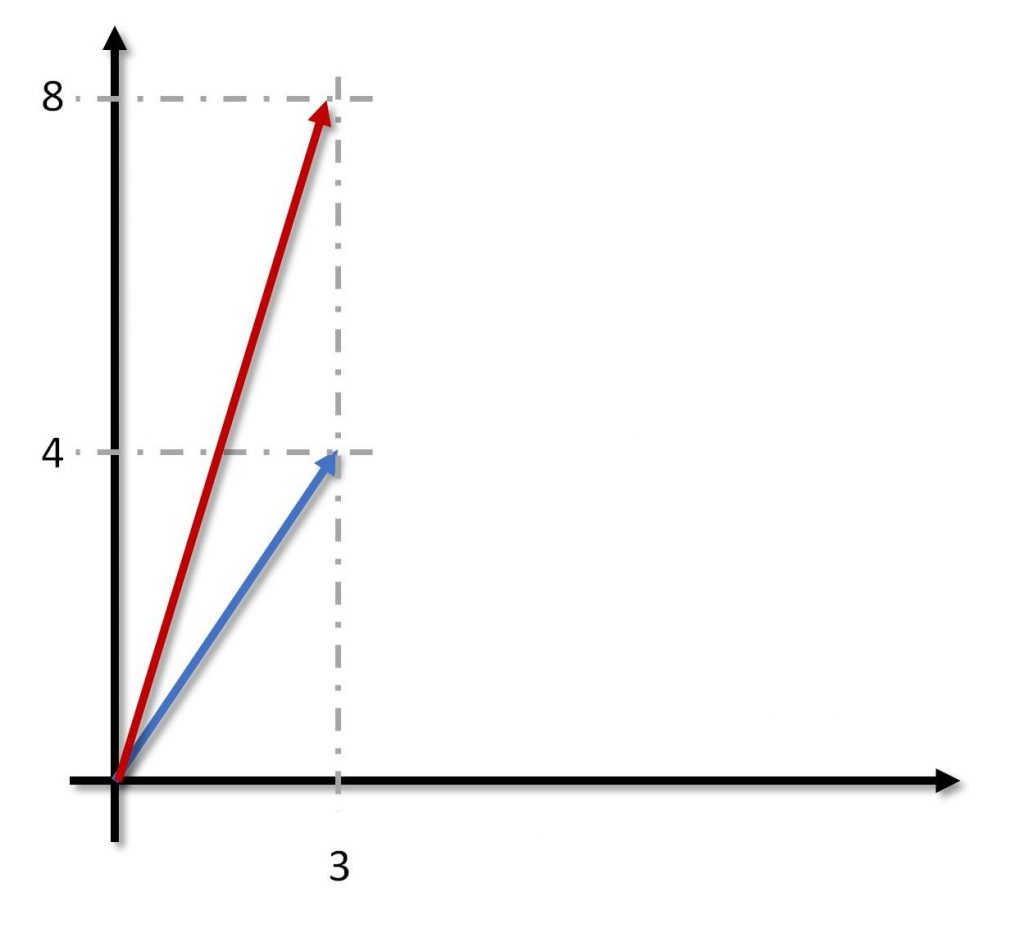
Figura 4: Allungamento di un vettore

Facciamo un esempio. Supponiamo, come nella Figura 4, di voler allungare un vettore, ma solo in altezza, diciamo di un fattore due. Dunque, dobbiamo moltiplicare per due la y e lasciare invariata la x. Se ricordiamo che il prodotto tra una matrice e un vettore si fa moltiplicando le righe della matrice con il vettore disposto a colonna, avremo:

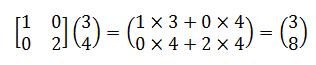
Che è esattamente ciò che volevamo. In base alla trasformazione che vogliamo applicare ad un vettore, possiamo creare la matrice opportuna. OpenCV ragiona esattamente in questo modo, come del resto la maggior parte delle librerie grafiche come OpenGl o DirectX. Quindi, ogniqualvolta vogliamo applicare una trasformazione ad un’immagine, ossia trasformare tutti i suoi punti, la libreria grafica in questione ci chiederà di fornire una matrice, e poi ci penserà lei ad applicarla. [...]

ATTENZIONE: quello che hai appena letto è solo un estratto, l'Articolo Tecnico completo è composto da ben 3285 parole ed è riservato agli ABBONATI. Con l'Abbonamento avrai anche accesso a tutti gli altri Articoli Tecnici che potrai leggere in formato PDF per un anno. ABBONATI ORA, è semplice e sicuro.

Ti potrebbe interessare anche:

Microcontrollori e crittografia

Sniffing su RS232: come si spiano le connessioni seriali

Monitoraggio IoT con i sistemi SCADA open source

Accendere e spegnere LED mediante i dispositivi ombra di AWS IoT

Progettare un robot pick and place in MATLAB/Simulink

Progetto di un misuratore di corrente elettrica basato sul sensore ad effetto Hall ACS712 – Parte 1