
La libreria di conversione in ambiente AVR che presenteremo in questo articolo è ready-to-run per essere utilizzata in applicazioni embedded e dispone di numerosi aspetti che la rendono davvero interessante.
Questa libreria di conversione, da rappresentazioni in virgola mobile a stringa, è stata studiata per sistemi embedded con ridotte dimensioni di memoria:
si quantifica un’occupazione di memoria di circa 6000 byte di memoria FLASH. Questo modulo software è stato testato e realizzato utilizzando l’ambiente di compilazione AVR-GCC. È necessario disporre di almeno due funzioni che stdlib.h mette a disposizione: ultoa e itoa. La funzione C che realizza la conversione è ftoa così come è mostrato nel listato 1.
#define SIZE_OF_MANTISSA 23
#define BITS_UNTIL_EXPONENT 23
#define BITS_UNTIL_SIGN 31
#include <stdlib.h>
#include “ftoa.h”
void ftoa
(
float fp,
char ch[]
)
{
long *fake_fp_pointer;
unsigned long fixed_point;
char sign;
char n;
char exponent;
#if USE_BASE_2_EXP == 0
char exponent_10x;
unsigned int m;
#if ALLOW_FULL_RANGE == 1
float max_value_10;
float max_value_2;
#else
unsigned long max_value_10;
unsigned long max_value_2;
#endif
char mult_or_divide;
#endif
/*Turn floating point to fixed point number, stored in type LONG
with the decimal point stored at this point: 1.00000, eg: 2452 is 0.02452
Algorithm used:
1] set n to 0
2] set F to 0
3] read nth bit counting from LSB of floating point number, if 1, add 1 to F
4] divide F by 2
5] Increment n
6] While still bits left to read, goto step 3
*/
fake_fp_pointer = &fp;
//1] set n to 0
n = 0;
//2] set F to 0
fixed_point = 0;
while (n < SIZE_OF_MANTISSA)
{
//3] read nth bit counting from LSB of floating point number, if 1,
// add 1 to F
if (((*fake_fp_pointer >> n) & 0x01) == 1)
{
fixed_point += 100000;
}
//4] divide F by 2
fixed_point = fixed_point >> 1;
//5] Increment n
n++;
}
//there is an extra 1 that is dropped by floating point
fixed_point += 100000;
//now convert the exponent to signed type
exponent = (unsigned char)(*fake_fp_pointer >> BITS_UNTIL_EXPONENT) - 127;
//finally set up sign of mantissa if applicable
if (((*fake_fp_pointer >> BITS_UNTIL_SIGN) & 0x01) == 1)
{
sign = ‘-‘;
}
else
{
sign = ‘+’;
}
//convert to a “normal” number if the number is smallish
#if USE_E_ONLY_WHEN_NEEDED == 1
if (exponent >= 0 && exponent <= 10)
{
fixed_point *= 1 << exponent;
return_string(sign, fixed_point, 0, 0, ch);
return;
}
if (exponent >= -10 && exponent < 0)
{
fixed_point /= 1 << (exponent * -1);
return_string(sign, fixed_point, 0, 0, ch);
return;
}
#endif
#if USE_BASE_2_EXP == 1
return_string(sign, fixed_point, 2, exponent, ch);
return;
#endif
/* Now all thats left is to convert this data:
fixed_point X 2^exponent to something like
fixed_point X 10^exponent, if you don’t care about converting the number
to an easier to use format, don’t continue this code, as its just
SLOW. Also, at this point the data is still accurate to about 6
significant digits. Past this point you should test as it won’t be...
*/
#if USE_BASE_2_EXP == 0
/*
use the following algorithm to convert the two numbers
1] Find a value of x so 10^x that is as small as possible, BUT still
bigger than 2^exponent
2] Divide 2^exponent by 10^x, store in m
3] Multiply mantissa by m
4] Add x10^x
BUT in our case m must be below 0.2 or the type long will overflow, so if m
is bigger than .2 we just use a bigger x
*/
/*
1] Find a value of x so 10^x that is as small as possible, BUT still
bigger than 2^exponent
as it turns out, dividing exponent by 3 using integer math is a pretty
good way to get a rough approximation of step 1 that seems to work*/
exponent_10x = exponent / 3;
step2:
mult_or_divide = 1;
/*this section can use floating point... HOWEVER if you don’t need to be able
to use large exponents, you could easily get away with non-floating point.
performs 10 (to the power of) exponent_10x, stored in max_value_10, but when
exponent_10x is negative it uses some tricks to always use multiplication
(this lets you use type unsigned long). */
max_value_10 = 1;
if (exponent_10x > 0)
{
n = 0;
while (n < exponent_10x)
{
max_value_10 *= 10;
n++;
}
}
else
{
n = exponent_10x;
while (n < 0)
{
max_value_10 *= 10;
n++;
}
mult_or_divide *= -1;
}
/*this section can use floating point... HOWEVER if you don’t need to be able
to use large exponents, you could easily get away with non-floating point.
performs 2 (to the power of) exponent, stored in max_value_2, but when th
exponent is negative it uses some tricks to always use multiplication (this
lets you use type unsigned long) */
max_value_2 = 1;
if (exponent > 0)
{
n = 0;
while (n < exponent)
{
max_value_2 *= 2;
n++;
}
}
else
{
n = exponent;
while (n < 0)
{
max_value_2 *= 2;
n++;
}
mult_or_divide *= -1;
}
/*
2] Divide 2^exponent by 10^x, store in m
again... this is a slow spot due to floating point, but you could
switch to fixed point to speed everything up if you wanted */
if (mult_or_divide == 1)
{
m = (max_value_2 / max_value_10) * 10000;
}
else
{
m = (max_value_2 * max_value_10) * 10000;
}
if (m > 20000)
{
exponent_10x++;
//if m is too big, we increase the exp and try again, although this should
//never happen it is a simple error checking
goto step2;
}
//3] Multiply mantissa by m:
fixed_point *= m;
//move decimal place around
exponent_10x = exponent_10x - 1;
/* Now fixed_point has the number exponent_10x has the exponent, so the final
number is sign fixed_point x10 ^ exponent_10x, and be sure to insert a decimal place between digit
5 and 6 (counting from the RIGHT) of fixed_point */
return_string(sign, fixed_point, 10, exponent_10x, ch);
#endif
return;
| Listato - Funzione di conversione |
Notazione in virgola mobile
Per comprendere pienamente la funzione ftoa è necessario rispolverare alcune considerazioni sulla notazione in virgola mobile. Un numero N in virgola mobile (espresso in una base B) può essere rappresentato nella seguente forma:
N = ± M * B ±E
dove M è la mantissa ed E è l’esponente del numero. Questo numero può essere memorizzato in una parola binaria di tre campi :
- Segno: più o meno.
- Mantissa: M.
- Esponente: E.
La base B è implicita e non deve essere memorizzata perché è la stessa per tutti i numeri. Si ricorre a questa rappresentazione (in inglese floating point) sia per poter definire numeri variabili in un campo di valori molto grande senza dover utilizzare un elevato numero di bit, sia per ottenere una coincidenza con il significato di numero reale nei più comuni linguaggi di programmazione. La figura 1 mostra un tipico formato a 32 bit in virgola mobile.
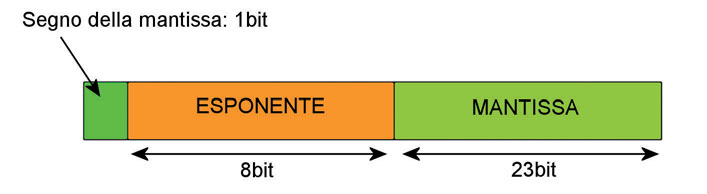
Figura 1: un tipico formato di numeri in virgola mobile a 32 bit.
Assumiamo che la base è 2, non è presente nella figura perché non va memorizzata. Il bit più a sinistra memorizza il segno del numero (0 per numero positivo, 1 per numero negativo). Il valore dell’esponente è memorizzato nei successivi 8 bit della rappresentazione. L’esponente, che può essere negativo o positivo, è rappresentato normalmente in forma polarizzata, ossia si somma al valore vero dell’esponente un numero tale da rendere nullo il massimo esponente negativo. Tipicamente il numero di polarizzazione vale 2k-1-1 (dove k è il numero di bit dell’esponente. Nella figura 1, gli 8 bit del campo coprono un intervallo che va da 0 a 255, ma con una polarizzazione di 127, i valori dell’esponente sono messi su un intervallo che va da –127 a 128. Questo tipo di rappresentazione ha il vantaggio di consentire di fare confronti tra due numeri in virgola mobile utilizzando l’aritmetica dei numeri interi, rendendo molto più semplice l’operazione. Infatti fare confronti tra due numeri con esponenti rappresentati con segno e valore o con i complementi è più complesso, in quanto bisogna separare le diverse parti e fare confronti parziali. Invece se si rappresentano i numeri in virgola mobile con il formato descritto nella figura e con gli esponenti polarizzati, la relazione di maggiore o minore che vige tra due numeri rimane valida anche se assumiamo che le due stringhe rappresentino due numeri interi, rappresentati con segno e valore assoluto. La parte finale della parola (in questo caso 23 bit) è la mantissa. La mantissa è rappresentata solitamente in valore assoluto. Se il bit più significativo della mantissa è 1 essa si dirà normalizzata. Per semplificare le operazioni sui numeri in virgola mobile, si richiede tipicamente che questi sia normalizzati. Un numero non nullo normalizzato assume la forma:
± 0,1bbbb…b * 2±E
dove b è una cifra binaria (0 o 1). Questo implica che la mantissa è sempre normalizzata, ha sempre il bit più significativo pari a 1 e quindi non è necessario memorizzarlo in quanto implicitamente presente. In questo modo, il campo a 23 bit può memorizzare in realtà una mantissa di 24 bit con valori tra 0,5 e 1. Alcuni esempi di numeri memorizzati in questo formato sono quelli di figura 4.

Figura 4: alcuni esempi di numeri espressi in virgola mobile a 32 bit.
Si notino le seguenti caratteristiche :
» il segno è memorizzato nel primo bit della sequenza;
» il primo bit della mantissa è sempre 1 e quindi non necessita che sia immagazzinato nel campo della mantissa;
» il valore 127 è aggiunto al vero valore dell’esponente e memorizzato nel campo dell’esponente;
» la base è 2.
Con questo formato in virgola mobile sono rappresentabili i seguenti intervalli di numeri:
» numeri negativi tra – (- 1 - 2-24) 2128 e -0,5 * 2-127
» numeri positivi tra 0,5 * 2-127 e (1 – 2-24 ) * 2128
Restano invece scoperti cinque intervalli che sono:
» numeri negativi minori di – (1 - 2-24) * 2128 detti overflow negativo (A);
» numeri negativi maggiori di – 0,5 * 2-127 detti underflow negativo (B);
» lo zero;
» numeri positivi minori di 0,5 * 2-127 detti underflow positivo (C);
» numeri positivi maggiori di (1 – 2-24) 2128 detti overflow positivo (D).
Queste relazioni sono illustrate nella figura 2.
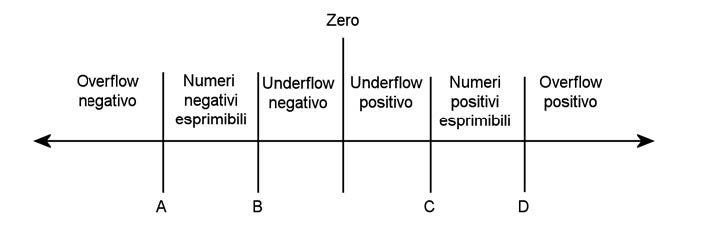
Figura 2: campo di rappresentazione dei numeri in virgola mobile.
Così come presentata, questa notazione non lascia spazio per un valore dello zero, ma le attuali rappresentazioni per i numeri in virgola mobile comprendono una sequenza speciale per lo zero. L’overflow avviene quando il risultato di un’operazione aritmetica è di una grandezza che non può essere espressa con un esponente di 128 (ad esempio ), mentre l’underflow avviene quando la grandezza della parte frazionale è troppo piccola (ad esempio 2). Tuttavia l’underflow è un problema meno serio dell’overflow in quanto il risultato può generalmente essere approssimato a zero in maniera soddisfacente. È importante notare che i numeri rappresentati in virgola mobile non sono distanziati uniformemente lungo la retta reale come lo sono i numeri in virgola fissa. I valori rappresentabili sono più compatti vicino all’origine e si diradano sempre più man mano che ci si allontana dalla figura 3.

Figura 3: densità dei numeri in virgola mobile.
Questo è un dei compromessi della matematica in virgola mobile: molti calcoli producono risultati che non sono esatti e devono essere arrotondati al valore più vicino che la notazione può rappresentare. Nel tipo di formato descritto in figura 1, c’è un compromesso tra l’intervallo di rappresentazione e la precisione e l’esempio mostra una rappresentazione in cui vengono dedicati 8 bit per l’esponente e 23 bit per la mantissa. Se si incrementasse il numero di bit nell’esponente, verrebbe espanso l’intervallo di rappresentazione, ma poiché possono essere espressi soltanto un numero fisso di valori diversi, verrebbe ridotta la densità di questi numeri e, quindi, la precisione. Il solo modo per aumentare sia l’intervallo di rappresentazione che la precisione è usare più bit. Per questo motivo, molti calcolatori forniscono per lo meno numeri a precisione singola e numeri a precisione doppia: ad esempio, un formato a precisione singola potrebbe usare 32 bit, mentre uno a precisione doppia ne potrebbe usare 64. Quindi c’è un compromesso tra il numero di bit nell’esponente ed il numero di bit nella mantissa.
La libreria software
Terminata questa breve dissertazione sui numeri a virgola mobile, occorre nella libreria di conversione, per prima cosa, definire le seguenti costanti:
- ALLOW_FULL_RANGE. Questa costante permette di definire la massima profondità dei valori rappresentabili. Infatti, con un valore pa
ri a 1 si permette di rappresentare fino a
20 cifre significative (per esempio 1e19), mentre con un valore pari a 0 si utilizza una bassa rappresentazione (1,234e4). Utilizzando una rappresentazione che contemplino poche valori di esponenti si ottiene un notevole risparmio di cicli macchina poiché in questo modo si risparmia una notevole quantità di operazioni di moltiplicazione. Il valore raccomandato per sistemi dedicati è un valore pari a 0;
- USE_BASE_2_EXP. Con un valore pari a 1 restituisce il valore dell’esponente del numero in base 2. Così restituisce il valore 1,245t10 da 1,245x2^10. Viceversa, con un valore pari a 0 il numero è restituito secondo il formato 1,245e5 in luogo di 1,245x10^5. Il suo valore raccomandato è un valore pari a 1;
- USE_E_ONLY_WHEN_NEEDED. Il valore di default di questa costante è pari a 1. Con il valore impostato a uno si restituirà il numero in notazione decimale e non visualizzerà la relativa notazione esponenziale. Non effettuando nessuna conversione si otterrà un significativo risparmio di tempo computazionale: un’ottimizzazione di tempo ma non di spazio. Il risparmio di spazio è invece relazionabile all’uso o meno della costante USE_2_EXP. Si nota che qualsiasi numero con una approssimazione 200 sarà restituito in un formato normale. Se si è consci di utilizzare numeri piccoli, può essere sufficiente impostare a uno USE_BASE_2_EXP e USE_E_ONLY_WHEN_NEEDED, in questo modo si ottimizzerà anche in spazio.
La funzione C delegata a questa particolare conversione ha il prototipo:
void ftoa
(
float fp,
char ch[]
);
Il listato 1 mostra l’intero sorgente e la sua lettura non presenta difficoltà anche per I vari commenti inseriti nel codice stesso. Questa libreria è stata messa a punto da Colin O’Flynn ed è distribuita secondo la formula definita come pubblico dominio e, in ragione di questo, chiunque può modificare questo modulo software senza incorrere a nessuna sanzione.




