
L'oggetto della sesta lezione del corso avanzato sul linguaggio C per Raspberry Pi è la ricorsione. Una strana e misteriosa argomentazione che rischia, spesso, di non essere ben compresa. La ricorsione è un metodo un po' strano, ma forse più naturale, per risolvere alcune classi di problemi. Vediamo come affrontarla senza fatica.
La ricorsione
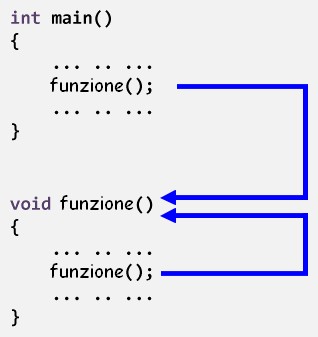
Con la ricorsione si possono definire e risolvere problemi tramite sé stessi. Si ha la ricorsione quando una funzione richiama sé stessa, ma non per un numero infinito di volte, come mostrato in figura 1. E' un potentissimo approccio di programmazione che consente la scrittura di algoritmi molto compatti ed efficienti. La ricorsione si ha anche in matematica, dove molte equazioni sono definite ricorsivamente. Si pensi, infatti, alla sequenza di Fibonacci:
F(i) = F(i-1) + F(i-2)
Vediamo, nei successivi capitoli, come definire in modo corretto un problema e come scrivere un codice senza errori. Per utilizzare la ricorsione occorre pensare in un modo diverso e, forse più semplice. Si dice che i bambini usano, spesso, codificare i propri pensieri in modo ricorsivo. Facciamo subito un esempio, riguardante la risoluzione di un algoritmo che consenta, a una persona, di ritornare a casa. La strategia ricorsiva prevede i seguenti compiti:
- ritornare a casa:
- se sei a casa, fermati. Sei arrivato;
- se non sei arrivato, cammina per un passo verso casa;
- quindi esegui il processo per ritornare a casa.
A prima vista l'algoritmo non contiene nessuna codificazione per cercare la strada di casa ma, guardando attentamente lo pseudo-codice, il succo dell'intera procedura è proprio contenuta lì dentro. Il primo passo da compiere è verificare che si sia arrivati già a casa, nel qual caso nulla dovrà accadere. Altrimenti occorre eseguire un passo verso casa semplificando, di fatto, le azioni da compiere, quindi ripetere l'intero algoritmo.
La struttura base di un algoritmo ricorsivo
Per iniziare bene a strutturare un algoritmo ricorsivo, è sufficiente tenere bene a mente i seguenti tre concetti base, con i quali organizzare il codice:
- la condizione di fermata, o di stop. Senza di essa si avrebbe un ciclo infinito (tautologia) che bloccherebbe, senz'altro, il computer;
- risolvere il problema esaminandolo e riducendolo all'osso, in maniera estremamente semplice;
- chiamata ricorsiva allo stesso algoritmo.
Il fattoriale di un numero
Bene, iniziamo subito a parlare di ricorsività andando a risolvere il calcolo del numero fattoriale, sempre indicato come primo esempio in questa casistica di argomentazione. Vedremo come affrontare la problematica scrivendo, prima, la codifica tradizionale e poi quella ricorsiva.
Ricordiamo, per tutti, che un numero fattoriale è definito come:
fattoriale(X) = X * (X-1) * (X-2) * ... * 2 * 1
Ad esempio, il fattoriale di 7 è uguale al prodotto di 7 per tutti i suoi numeri predecessori, fino a 1:
fattoriale(7) = 7 * 6 * 5 * 4 * 3 * 2 * 1 = 5040
Esso si indica anche con il punto esclamativo:
7! = 5040
Codifica tradizionale
Il sistema tradizionale prevede un ciclo che moltiplica il numero iniziale per un contatore sempre decrescente, fino a 1. Dal momento che si eseguono delle moltiplicazioni, è indispensabile inizializzare il valore del fattoriale a 1. Ecco di seguito il semplice codice.
/*
Calcolo tradizionale del
FATTORIALE
di un numero
di Giovanni Di Maria
*/
#include "stdio.h"
int main() {
int i,n;
unsigned long fattoriale;
fattoriale=1;
printf("\n\n Inserire il numero di cui si vuol calcolare il Fattoriale: ");
scanf("%d",&n);
for(i=n;i>=1;i--)
fattoriale*=i;
printf("\n\n Il fattoriale di %d e': %ld \n\n",n,fattoriale);
return 0;
}
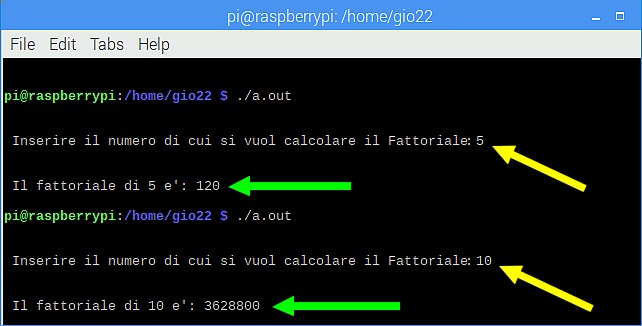
Eseguendo il programma sarà chiesto dal sistema il numero di cui si vuol calcolare il fattoriale, come si evince dalla figura 2.
Per la capienza intrinseca delle variabili di tipo unsigned long, il fattoriale massimo calcolabile è 12! pari a 479.001.600. Per valori più grandi la macchina va in overflow e inizia a fornire risultati inattesi.
Codifica ricorsiva
Vediamo, adesso, come si differenzia la codifica ricorsiva esaminando, poi, gli aspetti positivi e quelli negativi.
/*
Calcolo ricorsivo del
FATTORIALE
di un numero
di Giovanni Di Maria
*/
#include "stdio.h"
unsigned long fatt(int n);
int main() {
int n;
printf("\n\n Inserire il numero di cui si vuol calcolare il Fattoriale ");
scanf("%d",&n);
printf("\n\n Il fattoriale di %d e': %ld \n\n",n,fatt(n));
return 0;
}
unsigned long fatt(int n) {
unsigned long ritorno;
if(n==0)
ritorno=1;
else
ritorno=n*fatt(n-1);
return ritorno;
}
Esaminiamo il codice. La parte relativa agli input dei dati è sempre la stessa. Cambia invece il calcolo del fattoriale dedicato, stavolta interamente a una funzione UDF:
unsigned long fatt(int n) {
unsigned long ritorno;
if(n==0)
ritorno=1;
else
ritorno=n*fatt(n-1);
return ritorno;
}
Essa è estremamente ridotta e, in pratica, il suo enunciato è il seguente:
- Se il parametro passato alla funzione è pari a 0, il valore di uscita sarà 1. Questo perché, in matematica, il fattoriale di 0 è 1.
- Se, invece, il parametro passato non è zero, la funzione restituirà il valore della regola generale di n*(n-1)!
ATTENZIONE: quello che hai appena letto è solo un estratto, l'Articolo Tecnico completo è composto da ben 2215 parole ed è riservato agli ABBONATI. Con l'Abbonamento avrai anche accesso a tutti gli altri Articoli Tecnici che potrai leggere in formato PDF per un anno. ABBONATI ORA, è semplice e sicuro.







Personalmente evito sempre la ricorsione nei miei programmi. Ma per una mia formamentis mentale. Mi viene più semplice pensare in modo “procedurale” che non “ricorsivo”.
Articolo interessante che spiega in maniera chiara ed esaustiva il concetto di ricorsione. In matematica, ormai da molti anni, vengono studiati i cosiddetti sistemi di funzione iterate che sono alla base di sistemi caotici (si pensi alla famosa mappa logistica che simula la crescita di una popolazione di insetti). La ricorsività può essere definita anche localmente http://www.extrabyte.info/2017/02/09/funzioni-ricorsivamente-convergenti