
In questa puntata del corso esaminiamo le tecniche per ordinare, numericamente o alfabeticamente, le informazioni. Esistono tanti metodi per raggiungere lo scopo ma in linea generale non esiste la migliore tecnica in assoluto ma il risultato dipende, in buona parte, da come sono presentate le informazioni all'inizio della procedura.
Introduzione
Ci sembra un'operazione scontata, quella di trovare già alfabeticamente ordinata una lista di amici (vedi la rubrica del telefono cellulare) o, numericamente, la classifica del campionato. Su un foglio elettronico è sufficiente selezionare le righe da ordinare e scegliere l'opportuna operazione di sorting, per vedere ordinati, in pochi istanti, i propri dati. In effetti, se gli elementi da mettere in ordine sono pochi, diciamo non più di dieci, l'operazione potrebbe essere eseguita anche a mano. Ma sistemare un database composto da migliaia, se non da milioni, di records esige un algoritmo sicuro, affidabile e veloce. Esploriamo insieme alcune tecniche per scrivere un programma che ordini, numericamente o alfabeticamente, le informazioni immagazzinate in memoria.
Gli algoritmi per effettuare gli ordinamenti sono tantissimi, e in questa sede ne esploreremo solo alcuni. Tuttavia proponiamo, qui sotto, un elenco di alcuni metodi per il sorting dei dati:
- Selection Sort
- Bubble Sort
- Recursive Bubble Sort
- Insertion Sort
- Recursive Insertion Sort
- Merge Sort
- Iterative Merge Sort
- Quick Sort
- Iterative Quick Sort
- Heap Sort
- Counting Sort
- Radix Sort
- Bucket Sort
- ShellSort
- TimSort
- Comb Sort
- Pigeonhole Sort
- Cycle Sort
- Cocktail Sort
- Strand Sort
- Bitonic Sort
- Pancake sorting
- Binary Insertion Sort
- BogoSort or Permutation Sort
- Gnome Sort
- Sleep Sort
- Stooge Sort
- Tag Sort
- Tree Sort
- Cartesian Tree Sorting
- Odd-Even Sort / Brick Sort
- QuickSort on Singly Linked List
- QuickSort on Doubly Linked List
- 3-Way QuickSort
- Merge Sort for Linked Lists
- Merge Sort for Doubly Linked List
- 3-way Merge Sort
La ricerca dicotomica (o ricerca binaria)
Iniziamo con una tecnica di ricerca di una informazione all'interno di un archivio. Non si tratta di un ordinamento ma di una velocissima tecnica per rintracciare informazioni in un set di dati. Per la riuscita del metodo, occorre che il database sia già precedentemente ordinato. E' questa la condizione essenziale per cui la ricerca abbia successo in tempi istantanei e sbalorditivi, anche con archivi composti da mille miliardi di righe. La parola dicotomia vuol dire "tagliare in due parti diametralmente opposte" e tra poco si capirà il motivo di tale "taglio".
Il primo esempio della dicotomia prevede la ricerca di un numero, di cui si vuol conoscere la primalità, all'interno di un array. Se il numero cercato fa parte del set di dati, allora esso sarà un numero primo, altrimenti sarà un numero composto. Il vettore (visibile in figura 1) contenente le informazioni ha la seguente strutturazione:
[2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97];
In prima analisi, sarebbe sufficiente "scorrere" sequenzialmente tutto l'archivio, fino alla fine, per effettuare la ricerca del numero da testare. Questo approccio è accettabile solo se il numero di elementi è estremamente limitato ma se esso supera, diciamo, il miliardo, allora l'algoritmo inizia a farsi pesante. A ogni modo, qui sotto è proposto tale metodo, in maniera molto generale e senza l'adozione di ottimizzazioni. La variabile "da_cercare" contiene il numero di cui si deve verificare la primalità. Un ciclo attraversa l'intero vettore. Se durante la ricerca viene "pescato" un numero primo, un flag di controllo assume il valore "1" e tale valore resta per tutta l'esecuzione del programma. Viceversa, il valore del flag resterà "0". Alla fine, alcuni messaggi visualizzano il responso finale, proprio in dipendenza del contenuto di tale flag.
#include <stdio.h>
int main() {
int v[25] = {2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97};
int da_cercare = 67;
int flag_trovato = 0;
int k;
for(k=0;k<25;k++)
if(v[k]==da_cercare)
flag_trovato=1;
if(flag_trovato==0)
printf("Il numero %d e' un numero composto\n",da_cercare);
if(flag_trovato==1)
printf("Il numero %d e' un NUMERO PRIMO!!!\n",da_cercare);
return 0;
}
Se, ad esempio, il valore della variabile "da_cercare" è 67 (che è un numero primo), il messaggio di uscita sarà il seguente:
Il numero 67 e' un NUMERO PRIMO!!!
Se, invece, tale variabile contiene il valore 33 (che è un numero composto), il messaggio finale sarà il seguente:
Il numero 33 e' un numero composto
Come si buon ben capire, l'array non ha bisogno, in questo caso, di essere ordinato numericamente, in quanto la ricerca dell'eventuale numero primo avviene dal primo all'ultimo elemento, come bene evidenziato in figura 2.
Proprio per questo motivo, la complessità algoritmica di tale metodo è pari a:
O(n)
in quanto il numero di operazioni eseguite è, in pratica, proporzionale a N.
Vediamo, adesso, come effettuare una ricerca dicotomica, con tempi di elaborazione rapidissimi anche, come detto prima, per un numero estremamente elevato d'informazioni. Si ricorda che l'array deve essere necessariamente ordinato, in altre parole i valori devono essere immagazzinati dal più piccolo (all'indice 0) al più grande (all'indice 24).
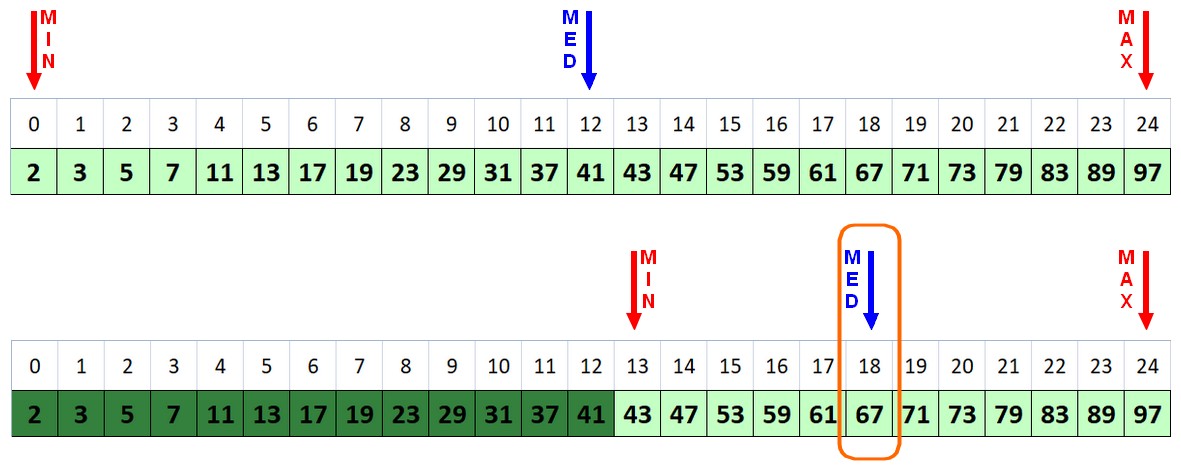
Si supponga di voler conoscere se il numero 67 è un numero primo. Occorre trovare l'elemento centrale del vettore, ossia quello che occupa la posizione:
v[(MAX+MIN)/2]
ossia:
v[(24+0)/2]
quindi:
v[12]
che corrisponde al numero 41. E' tale numero quello cercato? Evidentemente no, in quanto risulta minore di 67. Pertanto si deve effettuare una seconda ricerca tra la posizione dell'indice 13, corrispondente al numero primo 43 e la posizione dell'indice MAX, che corrisponde al numero primo 97. Questa volta, il valore contenuto in tale sotto vettore è pari a:
v[(MAX+PREV)/2]
ossia:
v[(24+13)/2]
quindi
v[18]
Il risultato 18.5 si può tranquillamente arrotondare per difetto, in quanto non esistono indici decimali in un array.
Il valore contenuto in questo elemento nell'array è proprio il numero 67. Dopo due soli tentativi si è trovata la risposta cercata. La figura 3 mostra chiaramente il processo seguito. In caso di ricerca di altri valori, i passi da compiere potrebbero essere di numero leggermente maggiore.
Esaminiamo uno pseudocodice per poi proporre il codice completo, in linguaggio C.
- poni minimo = 0 e massimo = n-1;
- se massimo < minimo, esci dal programma. Il numero non è presente in array;
- calcola la media degli indici come (minimo+massimo)/2;
- se v[media]=numero cercato, esci dal programma. Il numero primo è proprio quello;
- se v[media] < numero cercato, poni minimo = media + 1 (il numero primo è nella metà superiore dell'array);
- se v[media] < numero cercato, poni massimo= media -1 (il numero primo è nella metà inferiore dell'array);
- torna al punto 2.
Di seguito il listato minimale, ma perfettamente funzionante. E' possibile inserire qualche funzione di visualizzazione all'interno del ciclo, per tenere sotto controllo ciò che avviene durante l'elaborazione.
#include <stdio.h>
int main() {
int v[25] = {2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97};
int da_cercare = 89;
int minimo,massimo,mezzo;
minimo = 0;
massimo = 24;
while(1) {
mezzo = (minimo+massimo) / 2;
if(v[mezzo]==da_cercare) {
printf("Il numero %d e' un NUMERO PRIMO!!!\n",da_cercare);
break;
}
if(v[mezzo]<da_cercare)
minimo = mezzo + 1;
if(v[mezzo]>da_cercare)
massimo = mezzo - 1;
if(massimo<minimo)
break;
}
return 0;
}
In questo caso, i passi per rintracciare, eventualmente, il numero primo sono davvero pochi, anche per un numero elevatissimo di elementi. Proprio per questo motivo, la complessità algoritmica di tale metodo è pari a:
O(log n)
ATTENZIONE: quello che hai appena letto è solo un estratto, l'Articolo Tecnico completo è composto da ben 3038 parole ed è riservato agli ABBONATI. Con l'Abbonamento avrai anche accesso a tutti gli altri Articoli Tecnici che potrai leggere in formato PDF per un anno. ABBONATI ORA, è semplice e sicuro.









In quasi tutte le operazioni a MCU si trovano spesso le operazioni di Sort. Basti pensare, ad esempio, alla TV che presenta i canali ordinati secondo certi criteri, oppure il telefonino che ordina automaticamente i nominativi, in rubrica. A ogni modo, per un numero limitato di dati, qualunque tipologia di Sort è senz’altro adatta.