Nella precedente puntata “Corso di Elettronica per ragazzi - Puntata 12”, abbiamo approfondito i teoremi di Thevenin e Norton ed abbiamo eseguito una esercitazione teorica con un circuito di esempio con il quale abbiamo dimostrato come ottenere il circuito equivalente di Thevenin e di Norton. Inoltre, abbiamo completato la descrizione della realizzazione di un circuito amplificatore di corrente di cui abbiamo visto come calcolare il guadagno di corrente e le correnti d’ingresso e di uscita quando viene applicata una sorgente esterna di corrente all’ingresso dell’amplificatore e un carico resistivo posto ai due terminali di uscita. In questa nuova puntata introdurremo un altro importante principio: il “Principio di Sovrapposizione degli effetti”, un metodo molto utile nel semplificare l’analisi di circuiti e, conseguentemente, il calcolo di circuiti lineari complessi. Con questa puntata inizieremo una serie di esercitazioni partendo proprio da una esercitazione con il Principio di Sovrapposizione degli effetti. Oltre alla dimostrazione dell’uso del Principio di Sovrapposizione degli effetti, l’esercitazione avrà lo scopo di ripassare alcuni dei principali argomenti che abbiamo descritto nelle precedenti puntate. Questo ed altri esercizi sono necessari per prendere pratica con l’uso dei metodi di calcolo, ma anche per testare il livello di preparazione raggiunto dai partecipanti al corso al fine di verificare se siano pronti o meno ad affrontare i successivi argomenti più complessi nelle successive puntate del corso di elettronica. L’esercizio presentato in questa puntata e gli altri esercizi proposti in altre puntate, consisteranno nel calcolo di semplici circuiti resistivi lineari costituiti da generatori indipendenti e generatori controllati con cui ripasseremo i seguenti argomenti: la legge di Ohm, l’analisi nodale, le leggi di Kirchhoff, i teoremi di Thevenin e di Norton, la resistenza equivalente, il principio di Sovrapposizione degli effetti, i modelli equivalenti di amplificatori di tensione e di corrente con generatori controllati di tensione e di corrente.
Il Principio di Sovrapposizione degli effetti
Il concetto del Principio di Sovrapposizione degli effetti può essere intuito già dal nome stesso “Sovrapposizione degli effetti”. Infatti, se in un circuito in cui sono presenti generatori indipendenti di tensione e di corrente calcoliamo tensioni e correnti prodotte per “effetto” di un solo generatore per volta presente nel circuito, ovvero spegnendo tutti gli altri, possiamo affermare che l’effetto risultante possa essere la somma (appunto la sovrapposizione degli effetti) delle tensioni e correnti calcolate per ogni generatore indipendente. Da quanto detto, possiamo dare la definizione del Principio di Sovrapposizione degli effetti.
In un circuito resistivo lineare le tensioni e le correnti corrispondono alla somma delle tensioni e delle correnti determinate per effetto dell’azione di ogni singolo generatore indipendente mentre sono spenti tutti gli altri generatori indipendenti.
Ricordiamo che un generatore indipendente di tensione spento equivale ad un corto circuito la cui tensione (o differenza di potenziale) è nulla per qualsiasi corrente che lo attraversa, mentre un generatore indipendente di corrente spento equivale ad un circuito aperto in cui la corrente è nulla per qualsiasi tensione applicata.
Esercitazione con il Principio di Sovrapposizione degli effetti
Ora, vediamo con una esercitazione come utilizzare il Principio di Sovrapposizione degli effetti per calcolare tensioni e correnti di un circuito di esempio il cui schema elettrico è riportato in Figura 1.
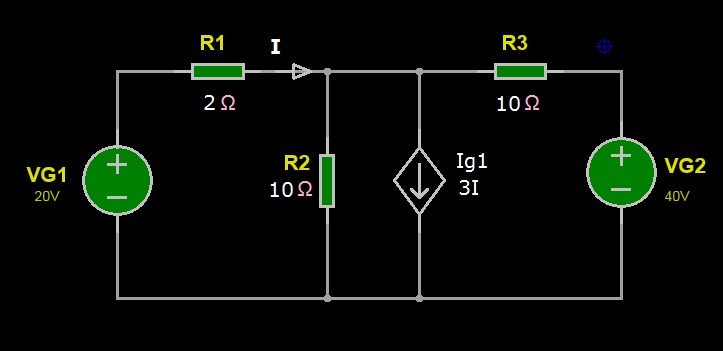
Figura 1: Circuito di esempio per il calcolo di tensioni e correnti con il Principio di Sovrapposizione degli effetti
Nel circuito di Figura 1 sono presenti due generatori indipendenti di tensione VG1 e VG2, un generatore dipendente di corrente Ig1 controllato in corrente e tre resistori. Il generatore di corrente Ig1 è controllato dalla corrente I, ovvero la corrente risultante del generatore di corrente Ig1 sarà equivalente al prodotto della corrente I per il coefficiente di amplificazione di corrente 3, infatti, il simbolo 3I indicato a fianco di Ig1 nello schema elettrico di Figura 1 sottintende il prodotto 3*I. In questo esercizio, vogliamo calcolare la corrente I che attraversa il resistore R1 utilizzando il Principio di Sovrapposizione degli effetti. Data la definizione del Principio di Sovrapposizione degli effetti, calcoleremo prima la frazione della corrente I, che chiameremo I1, determinata solo dall’effetto del generatore VG1, ossia spegnendo il generatore indipendente VG2; poi calcoleremo la frazione della corrente I, che chiameremo I2, determinata solo dal generatore VG2 spegnendo il generatore indipendente VG1; infine, faremo la somma algebrica delle correnti I1 e I2 per calcolare l’effettiva corrente I richiesta. Dunque, per calcolare la corrente I1, ovvero la frazione di corrente della I con il solo generatore indipendente VG1 presente nel circuito, spegneremo il generatore indipendente VG2 sostituendolo con un corto circuito, come mostrato nel circuito risultante di Figura 2.
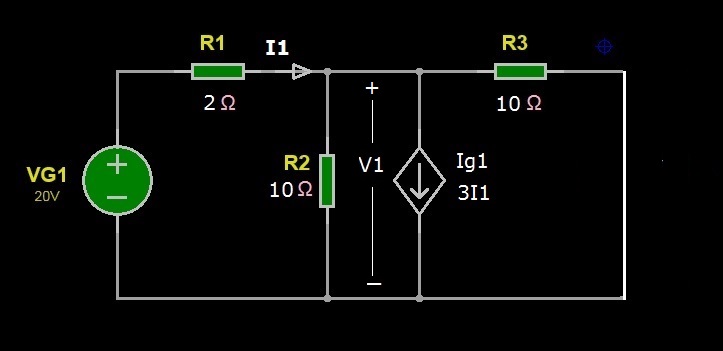
Figura 2: Circuito con VG2 spento per il calcolo della corrente I1
Possiamo subito notare che il circuito così modificato presenta i due resistori R2 e R3 in parallelo (hanno la stessa tensione ai loro terminali), inoltre, il generatore dipendente di corrente in questo caso è controllato dalla corrente I1. La Figura 3 mostra il circuito ridisegnato con i resistori disposti correttamente nello schema.
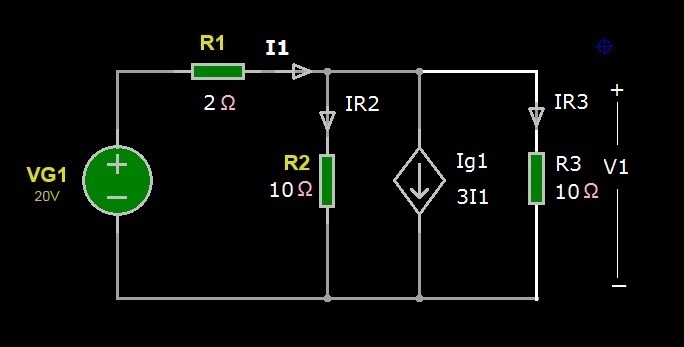
Figura 3: Circuito con R2 e R3 in parallelo con VG2 spento
Ricordiamo che la resistenza è l’inverso della conduttanza, ovvero G=1/R, per cui il calcolo della resistenza equivalente al parallelo di resistori si riduce all’inverso della somma delle conduttanze. Ad esempio, in un parallelo di due resistori, come nel nostro caso, la tensione ai capi del parallelo è la stessa per i due resistori, mentre la corrente entrante nel parallelo si dirama in due correnti, come illustrato nello schema di esempio di Figura 4.
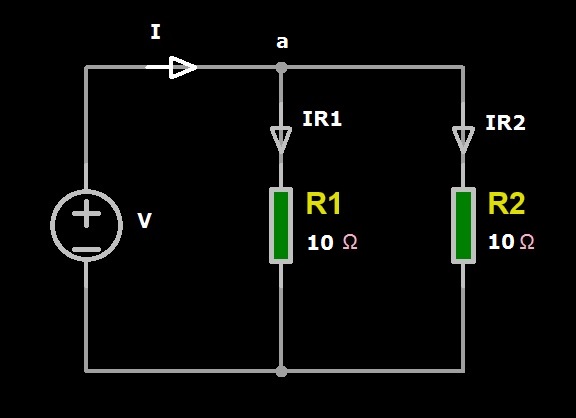
Figura 4: Resistori in parallelo
Applicando la LKC al nodo “a”, la corrente I entrante (positiva) è la somma delle correnti uscenti IR1 e IR2 che attraversano i due resistori, come definito dall’equazione seguente:
I=IR1+IR2
Essendo V del generatore la tensione ai capi dei resistori, dalla legge di Ohm possiamo riscrivere l’equazione della I così:
I=V/R1+V/R2 da cui per G=1/R I=G1*V+G2*V
Infine, abbiamo la conduttanza totale del parallelo dei due resistori, ovvero:
I/V=G1+G2
La resistenza corrispondente sarà quindi l’inverso della conduttanza totale:
V/I=1/(G1+G2)=1/(1/R1+1/R2)
Tornando al nostro circuito di Figura 3, denominate Rp la resistenza del parallelo dei due resistori e Ip la somma delle correnti IR2 e IR3, sostituendo i valori dei due resistori nell'equazione, otteniamo:
Rp=V1/Ip=1/(G2+G3)=1/(1/R2+1/R3)=1/(1/10+1/10)=1/(0,1+0,1)=1/0,2=5 ohm
Nel circuito di Figura 3 possiamo quindi sostituire R2 e R3 con un resistore da 5 ohm, come mostrato in Figura 5.
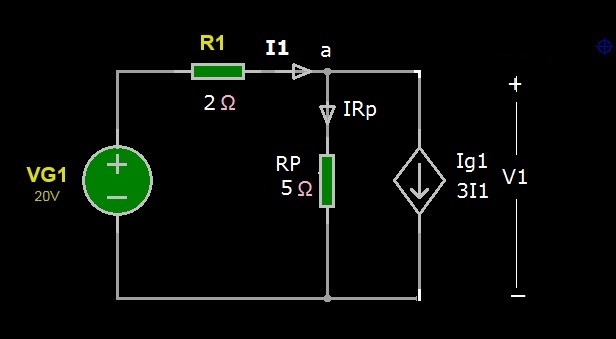
Figura 5: Circuito finale per il calcolo della corrente I1
A questo punto, possiamo calcolare la corrente I1 applicando la LKC al nodo “a”.
I1-IRp-3I1=0
Applichiamo la LKV alla maglia VG1-R1-V1:
VG1-R1*I1-V1=0 da cui I1=(VG1-V1)/R1
Pertanto, per risolvere la I1 dobbiamo calcolare la tensione V1, quindi tornando alla relazione delle correnti, si ha:
(VG1-V1)/R1-V1/Rp-3*(VG1-V1)/R1=0
Svolgendo le operazioni con le parentesi otteniamo i singoli termini contenenti V1:
VG1/R1-V1/R1-V1/Rp-3*VG1/R1+3*V1/R1=0
Mettendo in evidenza V1 alla sinistra del segno =, otteniamo la seguente equazione:
V1(3/R1-1/R1-1/Rp)=VG1(3/R1-1/R1)
Ora, possiamo ricavare V1:
V1=[VG1(3/R1-1/R1)]/[(3/R1-1/R1-1/Rp)]
Sostituendo i simboli con i valori numerici, si ottiene:
V1=[20(3/2-1/2) ]/[(3/2-1/2-1/5)]=20/0,8=25 V
Nota V1, possiamo calcolare la corrente I1:
I1=(VG1-V1)/R1=(20-25)/2=-2,5 A
Dal risultato ottenuto possiamo intanto notare che la corrente I1, essendo di valore negativo, ha verso opposto al verso della corrente I indicato nei circuiti fin qui mostrati. Ora, per completare il calcolo della corrente richiesta I, non ci resta che calcolare la corrente I2 con il solo generatore indipendente di tensione VG2 inserito e VG1 spento nel nostro circuito, come mostrato nello schema di Figura 6.
ATTENZIONE: quello che hai appena letto è solo un estratto, l'Articolo Tecnico completo è composto da ben 2439 parole ed è riservato agli ABBONATI. Con l'Abbonamento avrai anche accesso a tutti gli altri Articoli Tecnici che potrai leggere in formato PDF per un anno. ABBONATI ORA, è semplice e sicuro.