Corso di Elettronica per ragazzi – Puntata 19

Nella precedente puntata abbiamo descritto e analizzato il funzionamento dell’amplificatore non invertente e dell’amplificatore invertente. Di questi amplificatori abbiamo spiegato come rappresentare l’amplificatore operazionale mediante i circuiti equivalenti e come calcolare le correnti, la tensione di uscita, l’amplificazione di tensione, la resistenza d’ingresso e la resistenza di uscita. In questa puntata, continueremo lo studio dell’amplificatore operazionale con altri due esempi di utilizzo di questo importante dispositivo nei circuiti elettronici: l’amplificatore sommatore e l’amplificatore differenziale.

L’amplificatore sommatore

Inizieremo lo studio di applicazioni dell’amplificatore operazionale con l’amplificatore sommatore. Nella Figura 1 viene mostrato lo schema elettrico di un esempio di amplificatore sommatore.

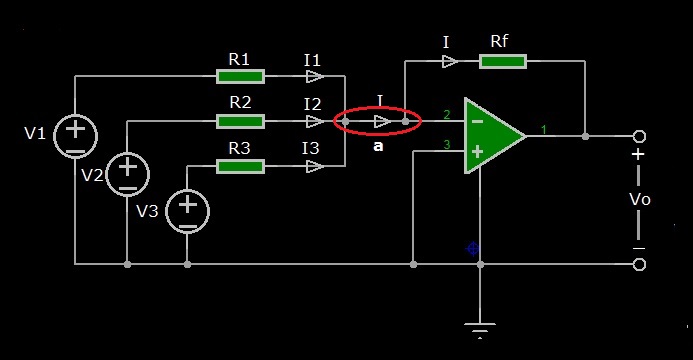
Figura 1: Schema elettrico di un amplificatore sommatore

L’amplificatore sommatore è un amplificatore invertente in grado anche di sommare più segnali applicati in ingresso. Come esempio, nello schema di Figura 1 abbiamo collegato all’ingresso dell’amplificatore invertente tre generatori di tensione indipendenti V1, V2 e V3 collegati ai rispettivi terminali dei resistori R1, R2, e R3, mentre gli altri terminali sono collegati insieme al terminale negativo dell’operazionale.

Lo schema è già pronto per la nostra analisi, in quanto, come vedete sono indicate la tensione di uscita Vo, le correnti con il loro verso, I1, I2, e I3, confluenti in entrata nel nodo “a” e la corrente I somma delle tre correnti, uscente dal nodo “a” e diretta verso il resistore Rf di controreazione (in inglese “feedback”). Notate che il nodo “a” è in pratica coincidente con i due nodi inclusi nell’ellisse. Ora, applicheremo l’analisi nodale per calcolare le correnti considerando, come al solito, ideale l’amplificatore operazionale, a meno che venga dichiarato reale all’occorrenza.
Applichiamo la LKC al nodo “a” considerando positive le correnti entranti e negative le correnti uscenti dal nodo:

I1+I2+I3-I=0

Considerando che i due terminali d’ingresso dell’operazionale “+” e “-“ sono in cortocircuito virtuale, e dato che il terminale positivo è a massa, il terminale negativo è a massa virtuale, applicando la legge di Ohm ricaviamo le correnti e le sostituiamo nell’equazione precedente delle correnti:

I1=V1/R1, I2=V2/R2, I3=V3/R3, I=-Vo/Rf

Quindi, tornando alla prima equazione si ha:

V1/R1+V2/R2+V3/R3+Vo/Rf=0

A questo punto, da quest’ultima equazione possiamo ricavare la tensione di uscita Vo:

Vo=-Rf*(V1/R1+V2/R2+V3/R3)

Si noti il segno negativo della tensione di uscita che sta ad indicare che l’amplificatore sommatore, essendo costituito dall’amplificatore operazionale invertente, inverte in uscita il verso del segnale d’ingresso.

Possiamo scrivere questa relazione anche così:

Vo=-(V1*Rf/R1+V2*Rf/R2+V3*Rf/R3)

In questo modo, vediamo più chiaramente che il valore di Vo per ogni segnale d’ingresso del generatore applicato dipende dal rapporto fra la resistenza di controreazione Rf e la resistenza collegata al rispettivo generatore. In pratica, definita Rx la resistenza collegata al generatore Vx, il rapporto Rf/Rx può essere considerato il coefficiente di amplificazione di tensione dell’amplificatore sommatore, ovvero, quando Rf>Rx l’amplificatore amplifica il segnale d’ingresso, mentre per Rf<Rx l’amplificatore attenua il segnale d’ingresso. Si ottiene il guadagno unitario e l’inversione del segnale d’ingresso per Rf=Rx, ossia Vo=-Vx.

L’amplificatore differenziale

Un altro utilizzo dell’amplificatore operazionale è quello di realizzare un amplificatore differenziale. Il funzionamento di questo tipo di amplificatore è dedotto proprio dalla parola “differenziale”: l’amplificatore differenziale effettua la differenza fra i segnali applicati ai due terminali d’ingresso “+” e “-”dell’operazionale.

Nella Figura 2 viene mostrato lo schema teorico di un amplificatore differenziale.

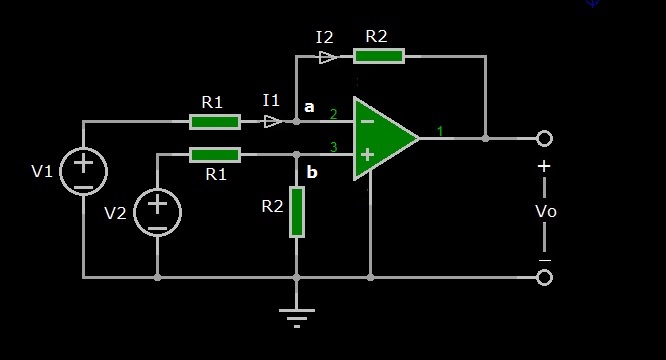
Figura 2: Amplificatore differenziale

Ci poniamo ora l’obiettivo di calcolare la risposta del circuito all’applicazione dei due segnali d’ingresso V1 e V2, ovvero la tensione di uscita Vo. Indichiamo con Va la tensione fra il terminale “-” (nodo a) e massa, e con Vb la tensione fra il terminale “+” (nodo b) e massa. Applichiamo la LKV alla maglia Va-R2-Vo per calcolare la corrente I2:

Vo+R2*I2-Va=0

Isoliamo a sinistra il termine contenente la corrente I2:

R2*I2=-Vo+Va

Con la legge di Ohm calcoliamo la corrente I2:

I2=(-Vo+Va)/R2

Ricordando che i terminali “+” e “-” dell’operazionale sono in cortocircuito virtuale e non fluisce corrente attraverso essi, applichiamo la LKC al nodo “a” scegliendo positive le correnti entranti e negative le correnti uscenti dal nodo:

I1-I2=0

Applichiamo la LKV alla maglia V1-R1-Va per calcolare la corrente I1:

V1 -R1* I1-Va=0

Isoliamo a sinistra il termine contenente la corrente I1:

R1*I1=V1-Va

Con la legge di Ohm calcoliamo la corrente I1:

I1=(V1-Va)/R1

Poi sostituiamo I1 e I2 nell’equazione delle correnti I1-I2=0:

(V1-Va)/R1-(-Vo+Va)/R2=0

Da quest’ultima relazione, dopo qualche passaggio, ricaviamo Vo:

(-Vo+Va)/R2=(V1-Va)/R1

Svolgiamo le operazioni con le parentesi:

-Vo/R2+Va/R2=V1/R1-Va/R1

Isoliamo a sinistra Vo:

-Vo/R2=-Va/R2+V1/R1-Va/R1

Moltiplicando i due termini dell’uguaglianza per R2:

-Vo=-Va+V1*R2/R1-Va*R2/R1

Mettiamo in evidenza Va:

-Vo=-Va(1+R2/R1)+V1*R2/R1

Cambiamo segno ai due termini dell’uguaglianza moltiplicandoli per -1:

Vo=Va(1+R2/R1)-V1*R2/R1

A questo punto, calcoliamo la tensione Vb al terminale “+” mediante il partitore di tensione R1-R2 su V2:

Vb=V2*R2/(R1+R2)

Ora, ricordando ancora che i due terminali “+” e “-” sono in cortocircuito virtuale, si ha:

Va=Vb

Quindi, nella precedente espressione di Vo possiamo sostituire Va con la relazione di Vb:

Vo=V2*R2/(R1+R2)*(1+R2/R1)-V1*R2/R1

Svolgendo la moltiplicazione si ottiene la seguente espressione:

Vo=V2*R2/R1-V1*R2/R1

Mettendo in evidenza R2/R1 si ricava la relazione finale di Vo:

Vo=R2/R1*(V2-V1)

Quest’ultima relazione rappresenta proprio la funzione dell’amplificatore differenziale, ossia amplificare la differenza dei segnali applicati ai due ingressi dell’operazionale. Questa funzione è molto importante poiché permette di amplificare solo valori differenti di due segnali eliminando un eventuale segnale indesiderato (ad esempio interferenze o disturbi) comune ai due ingressi. Infatti, se ad esempio i segnali V1 e V2 fossero identici, ossia con lo stesso valore di tensione e verso, la tensione di uscita Vo sarebbe nulla. Nella formula di Vo il termine R2/R1 è il coefficiente di amplificazione (o guadagno) che chiamiamo Ad della tensione differenza d’ingresso:

Ad=Vo/(V2-V1)=R2/R1

La proprietà dell’amplificatore differenziale di eliminare i segnali di disturbo è molto rilevante in quanto questo tipo di amplificatori è utilizzato maggiormente nella strumentazione di misura di precisione. Occorre però tener presente che quanto fin qui esposto è confermato dai calcoli solo nell’ipotesi che le due resistenze R1 e le due resistenze R2 siano identiche, ovvero, il risultato ottenuto è valido in via teorica poiché, per quanto possano essere precisi i valori di resistenza dei resistori R1 e R2, la tolleranza dei valori delle resistenze non potrà mai garantire valori identici teorici. Un altro importante aspetto da considerare di questa configurazione circuitale di amplificatore differenziale è la bassa resistenza d’ingresso, tipica dell’amplificatore invertente.

Resistenza differenziale

Vogliamo dunque andare a “vedere” la resistenza d’ingresso (o resistenza differenziale) tra i due terminali d’ingresso dell’amplificatore differenziale. Per fare questo, riconsideriamo il circuito di Figura 2 ponendo al posto dei due generatori di tensione un unico generatore di tensione indipendente il cui valore di tensione è la differenza V2-V1 che chiameremo Vd, come mostrato in Figura 3.

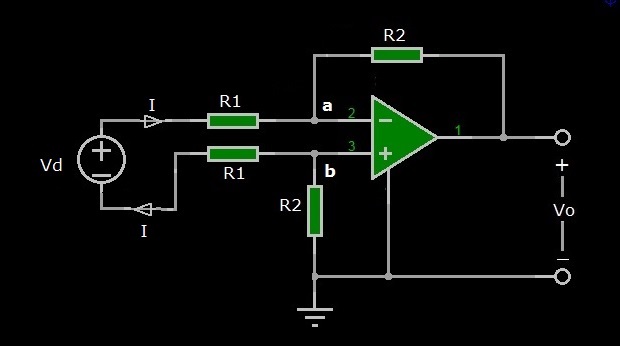
Figura 3: Amplificatore differenziale con generatore differenziale d’ingresso

La resistenza d’ingresso “vista” fra i due terminali “+” e “-” (in cortocircuito virtuale) si calcola con la relazione seguente:

Rin=Vd/I

Applichiamo la LKV alla maglia Vb-R1-Vd-R1-Va:

Vb-R1*I+Vd-R1*I-Va=0

Per il cortocircuito virtuale fra i nodi a e b, si ha Va=Vb, pertanto:

Vd=2*R1*I

Da quest’ultima relazione ricaviamo infine la Rin:

Rin=2*R1

Ricordando che il guadagno di tensione dell’amplificatore differenziale è R2/R1, si comprende che per avere un guadagno abbastanza elevato occorre che la resistenza d’ingresso (la R1*2) sia più bassa possibile. Ma sappiamo che per un amplificatore una bassa resistenza d’ingresso può essere un problema, specialmente quando viene utilizzato nella strumentazione. Quindi, quando viene richiesto che un amplificatore differenziale abbia una resistenza d’ingresso alta occorre prevedere una soluzione circuitale diversa e un pò più complessa, come vedremo nel prossimo esempio in cui descriveremo il progetto di un amplificatore differenziale per strumentazione.

Progetto di un amplificatore differenziale per strumentazione

Il circuito del progetto che andremo ad analizzare è un classico esempio di amplificatore differenziale per strumentazione che si trova spesso nella letteratura elettronica, nei testi di elettronica degli istituti tecnici elettronici e nei manuali universitari. Spesso utilizzata nella strumentazione come amplificatore per piccoli segnali analogici, la configurazione circuitale dell’amplificatore differenziale presentata in Figura 4 è un pò più complessa rispetto al circuito di amplificatore differenziale a singolo operazionale che abbiamo trattato in precedenza, ma risolve il problema della bassa resistenza d’ingresso e consente la regolazione del guadagno con facilità.

[...]

ATTENZIONE: quello che hai appena letto è solo un estratto, l'Articolo Tecnico completo è composto da ben 2670 parole ed è riservato agli ABBONATI. Con l'Abbonamento avrai anche accesso a tutti gli altri Articoli Tecnici che potrai leggere in formato PDF per un anno. ABBONATI ORA, è semplice e sicuro.