Avere a disposizione dei qubit è solo metà della questione; poi, con questi, bisogna farci qualcosa. Ovviamente, essendo i qubit oggetti particolari, potete aspettarvi che anche i circuiti che li manipolano siano un pò sui generis. Così è, infatti. Ma da grandi poteri derivano grandi opportunità e, come cercherò di raccontarvi oggi, il fatto di dover lavorare su oggetti quantistici aggiunge ulteriori vantaggi a quelli che abbiamo già visto. Il problema resta sempre quello: è tutto un altro mondo. Scordatevi tutto ciò che sapete di elettronica e seguitemi in questo nuovo, assurdo, paese delle meraviglie.
LA SCATOLA DEI GIOCHI
Se vi dovessi chiedere qual è il gioco che secondo voi ricorda più da vicino la progettazione dei circuiti elettronici, cosa mi rispondereste? Per quanto mi riguarda, non ci sono dubbi: Lego. Hai un certo numero di mattoncini a tua disposizione e li devi/puoi combinare a piacimento così da ottenere qualcosa di più grande. Con i circuiti, in fin dei conti, è lo stesso. Hai un certo numero di componenti e li puoi/devi combinare per arrivare ad avere qualcosa di più. Devo separare queste linee; ok, ci metto un multiplexer. Però questo multiplexer non deve essere sempre attivo, quindi qui ci metto un pò di porte, e via di questo passo. A differenza dei Lego, quando si ha a che fare con un circuito, non sempre ci sono le istruzioni a disposizione ma, se mi concedete questo volo di immaginazione, il concetto è quello.
C’è un’altra somiglianza che riguarda più da vicino quello di cui intendo parlarvi oggi, ossia che in entrambi i casi non abbiamo un insieme infinito di componenti diversi. Abbiamo un pò di mattoncini di base e un pò di porte logiche di base. Il motivo è semplice ed è lo stesso in entrambi i casi: i costi di produzione. Meno sono i mattoncini diversi, più potremo riusare sempre le stesse macchine per stamparli, e meno ci costerà il singolo mattoncino. Meno sono le porte logiche di base, più potremo riutilizzare sempre gli stessi processi tecnologici per realizzarle, e meno ci costerà il singolo circuito.
Ha senso, quindi, chiedersi quale sia il numero minimo di componenti che ci servano per fare… bè, tutto. Ovviamente non ha senso produrre un insieme di componenti che ci limiti nelle cose che possiamo realizzare. Nel caso dei circuiti, non ci vuole molto per dimostrare che possiamo fare tutto con due sole porte logiche, la AND e la NOT. Per motivi di prestazioni, all’atto pratico i processi tecnologici sono in grado di implementare anche altre porte, magari meno fondamentali dal punto di vista teorico ma che è bene ottimizzare un pò. Tipo i flip-flop, o certe combinazioni di porte che capitano di frequente, come la AND-OR-NOT. Tutte le altre porte poi vengono riportate a queste da particolari algoritmi che lavorano in incognito all’interno dei vari ambienti di sviluppo con cui si possono progettare circuiti.
Un discorso simile vale anche per i circuiti quantistici. Anche in questo caso ha senso cercare un insieme minimo di porte con cui possiamo fare tutto, dal momento che già è difficile realizzarlo, un qubit, figuriamoci duecento tipi diversi. Anche se spero di avervi convinto la volta passata che un bit sempre un bit è, indipendentemente da come lo si realizza, nel caso dei circuiti quantistici non possiamo usare le stesse porte dei circuiti “classici”. I qubit non si accontentano di AND e NOT, vogliono il loro insieme minimo di porte quantistiche. E il motivo fondamentale per cui AND e NOT non bastano è che le operazioni sui qubit, a differenza di quelle sui livelli di tensione, sono reversibili.
IL DIAVOLO E’ NEI DETTAGLI
Le persone normali non sfuggono all’età; i fisici non sfuggono al secondo principio della termodinamica. A seconda di chi lo enuncia, il secondo principio della termodinamica è quello che ci dà la freccia del tempo, che ci dice che un uovo che si rompe non tornerà mai spontaneamente intero e che se abbandonate la vostra camera a se stessa di sicuro non si metterà in ordine da sola. Come in quasi ogni altra cosa, i fisici enunciano leggi e principi sulla base di ciò che osservano: la natura si comporta così, punto. E al solito, il problema sorge quando ci si comincia a porre la domanda fatidica. Perché?
Perché un uovo non riuscirà mai a ricomporsi da solo? Ok, il processo di auto-ricostruzione richiede energia che l’uovo di suo non ha, ma del resto anche il processo di rottura ne richiede, e l’uovo non ha nemmeno quella. Che differenza c’è, quindi, nei due casi?
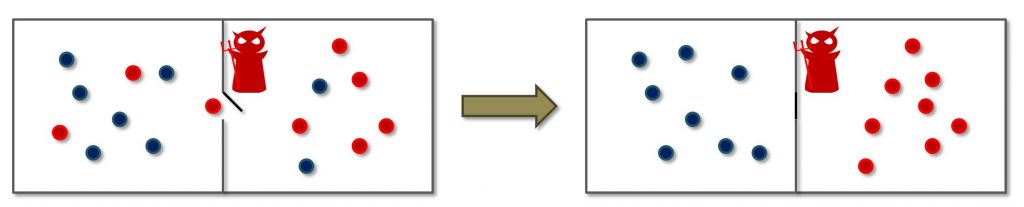
Figura 1: Il diavoletto di Maxwell
Il problema è noto da un bel pezzo. Maxwell, tempo che fu, se ne venne fuori con il famoso esempio del diavoletto. Come nella Figura 1, abbiamo un gas in un contenitore diviso in due parti separate da una piccola botola che il nostro diavoletto può controllare a piacimento. All’equilibrio termico, e con la botola aperta, il gas si distribuirà equamente nelle due metà. Ora, il diavoletto ha la vista acuta. Quando vede una molecola con velocità un pò maggiore delle altre dirigersi verso la botola, la apre immediatamente e la fa passare dall’altra parte. Visto che molecole più agitate implicano un gas a temperatura più alta, continuando con questo giochetto di selezione delle molecole più veloci, il diavoletto riuscirà ad aumentare la temperatura di una metà del gas e ad abbassare quella nell’altra metà. Con il gradiente termico che si viene così a creare tra le due metà si può compiere del lavoro; supponendo che la botola sia così ben fatta che non occorra lavoro per muoverla, il diavoletto riuscirà a creare lavoro senza sprecarne, il che, come purtroppo sappiamo, non è possibile.
Ma, di nuovo, perché? Perché il diavoletto riesce a creare ordine dal caos e l’uovo no? La differenza, per quanto strano possa sembrare, è che il diavoletto è intelligente, l’uovo no. Il diavoletto riesce nel suo intento perché sa quando e come muovere la botola per rimettere le molecole a posto; l’uovo non sa ricostruirsi da solo. Non sto dando i numeri. Quello che sto cercando di dire è che un processo è irreversibile quando, durante il suo svolgimento, viene persa informazione. L’uovo non ha informazione su come era fatto prima, quindi non ha speranze di tornare integro; il diavoletto sa quali sono le molecole a più alta temperatura e può rimetterle a posto.
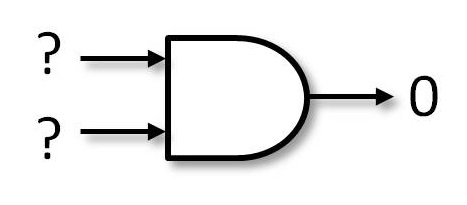
Figura 2: Che ingressi avevo?
Un esempio un pò meno astratto: la AND della Figura 2. La commutazione di una AND è un processo reversibile o irreversibile? Bè, se l’uscita è un uno, sappiamo per certo che gli ingressi erano entrambi a uno, ma se l’uscita è a zero, non possiamo sapere, in nessun modo, se gli ingressi erano entrambi a zero, o solo uno dei due lo era, e quale. Abbiamo perso informazione. Non si scappa. Prima conoscevamo entrambi gli ingressi, adesso non li conosciamo più. Non possiamo infilare uno zero nell’uscita della AND e ritrovare in ingresso gli ingressi che quello zero l’hanno generato.
Praticamente tutte le porte logiche comuni sono irreversibili, a parte la NOT. In generale, tutte quelle che hanno meno uscite che ingressi lo sono, a meno di non avere ulteriori informazioni sugli ingressi. Ad esempio, se sapessimo che il secondo ingresso deve essere necessariamente a uno, potremmo ricostruire l’altro ingresso dalla sola conoscenza dell’uscita. Questo, però, significa solo che all’inizio avevamo più informazione, e che in questo modo riusciamo a tamponare quella persa durante la commutazione della porta, non che la perdita di informazione non c’è stata.
Ora, sorpresa: i circuiti quantistici sono reversibili. Tutti quanti. Questo, se ci pensate un attimo, è fantastico. Un uovo che si rompe rilascia nell’ambiente l’energia di legame che teneva insieme i suoi pezzi. Un processo reversibile non rilascia calore verso l’ambiente. Nella maniera più assoluta. Per dirla in due parole, un computer quantistico non scalda. Non credo ci sia bisogno che vi dica perché questo è fantastico.
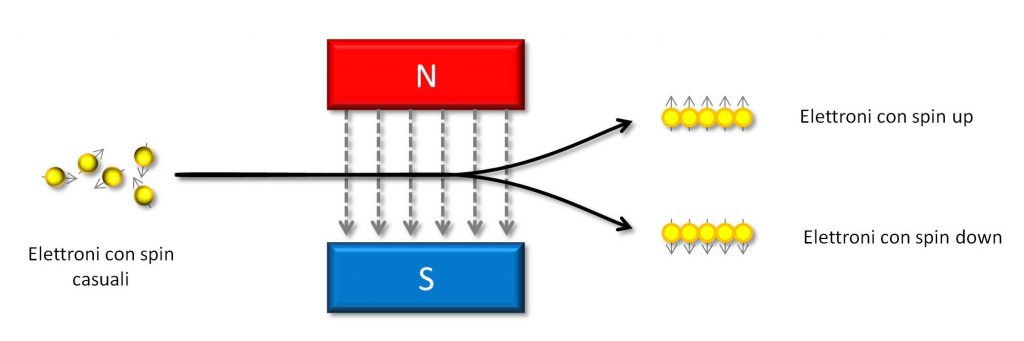
Figura 3: Elettroni in un campo magnetico
Perché i circuiti quantistici siano reversibili però vorrei cercare di spiegarvelo. Un circuito quantistico è un qualcosa che effettua delle operazioni sui qubit, giusto? Bene. Riprendiamo l’esempio del fascio di elettroni in un campo magnetico (Figura 3). Che operazioni possiamo compiere su questi qubit? Bè, ad esempio, potremmo pensare di ruotare l’apparato di novanta gradi, così da avere i due magneti, invece che sopra e sotto il fascio, a destra e a sinistra. In questo caso non ci aspettiamo più di avere sullo schermo alla fine dell’apparato, un mucchietto di elettroni sopra e uno sotto; ne avremo semmai uno a destra e uno a sinistra.
Ruotiamo ancora l’apparato, di altri novanta gradi. Avremo adesso il polo nord sotto e quello sud sopra, ma alla fine della festa continueremo ad avere un mucchietto sopra e uno sotto, ossia come al punto di partenza. In pratica, la prima rotazione ha trasformato lo spin up e lo spin down in spin “destra” e spin “sinistra”, e la seconda ha ri-trasformato di nuovo spin “destra” e “sinistra” in up e down. Questo vale in generale per le operazioni sui qubit, che possiamo vedere sempre come qualche genere di rotazione.
Ok, è un’affermazione un pò forte e non tanto intuitiva. Se vedessimo lo spin come il verso di rotazione dell’elettrone attorno al suo asse (cosa che non è), con esempi del genere avremmo difficoltà a spiegare come mai due rotazioni di un angolo diverso da novanta gradi riportino lo spin alla condizione di partenza. In effetti la cosa è un pò più sottile, ma non voglio ammorbarvi con la matematica. Cercate di convincervene pensando che alla fine allo spin, più che farlo ruotare e spostare i mucchietti in giro, non potete fargli molto altro.
NUOVI MATTONCINI
Ora, le rotazioni sono indubbiamente reversibili: se si conosce l’angolo di rotazione (e questa è un’informazione insita nel tipo di porta che si sta usando), si può di sicuro applicare una rotazione inversa e tornare allo stato di partenza. Il problema è che esiste un numero infinito di rotazioni, tanti quanti gli angoli di cui si può pensare di ruotare, e questo si scontra con il volere un set limitato di porte da cui partire per il progetto. Nel contesto dei circuiti quantistici, quindi, ciò che si va a cercare è l’insieme di porte in grado di approssimare adeguatamente, in un numero decente di passaggi, qualsiasi altra rotazione. [...]
ATTENZIONE: quello che hai appena letto è solo un estratto, l'Articolo Tecnico completo è composto da ben 2634 parole ed è riservato agli ABBONATI. Con l'Abbonamento avrai anche accesso a tutti gli altri Articoli Tecnici che potrai leggere in formato PDF per un anno. ABBONATI ORA, è semplice e sicuro.