Si dice che il mondo è bello perché è vario, ed è sicuramente così. Sembra, però, che ci sia almeno una cosa, nel mondo, senza particolare varietà: l’elettronica. Praticamente tutta l’elettronica che conosciamo e che usiamo è basata sul silicio. Ma perché? Perché è la strada migliore? Dopotutto, sono decenni che si sente parlare di questi favolosi “computer quantistici”, che ci permetteranno di risolvere problemi tuttora insolubili e non si sa bene che altro. Ma dove sono? La ricerca sembra continui, per cui si deve trattare di qualcosa di effettivamente interessante. Ma perché non li abbiamo ancora tra noi? Perché, come scoprirete oggi, si tratta davvero di oggetti con enormi potenzialità ma basati su un mondo molto diverso da quello cui siamo abituati.
A GAME OF POOL
Sapreste costruire un computer utilizzando solo delle palle da biliardo? Sì? No? Forse? Impossibile? Assurdo? Una follia? Sicuramente non è impossibile, anche se magari è un pò assurdo e, preso così com’è, probabilmente un pò folle, ma ha il suo perché. E questo perché è il rendersi conto del fatto che in realtà tutta la nostra tecnologia si basa sul silicio, banalmente perché non abbiamo trovato niente di meglio, ma non perché si possa fare solo con il silicio. Un computer, in quanto macchina per fare conti, è banalmente un insieme di bit e un insieme di circuiti per elaborarli. Ma in effetti, cos’è un bit? Potete mostrarmene uno? Potete prenderne uno e mettermelo in un piatto? Potete dire "guarda che bel bit, questo qui" ? I bit non esistono. I bit sono astrazioni, lo 0 e l’1 su cui diciamo che i computer lavorano sono delle etichette che associamo a dei particolari valori di tensione in particolari punti di un circuito. Al massimo potreste dire: "guarda che bel mucchietto di elettroni che ho qui", oppure "qua di elettroni ce ne sono davvero pochi", non molto di più.

Figura 1: Richard Feynman
Il soggetto nella Figura 1, un volto ricorrente in questo e in molti altri contesti, all’inizio del capitolo sul calcolo tensoriale delle sue famose lezioni di fisica dice che “i fisici prendono un caso particolare della realtà e la chiamano "fisica"; poi arrivano i matematici e generalizzano tutto”. Nulla di più vero. Viviamo sommersi di astrazioni e non ce ne rendiamo nemmeno conto, ma le astrazioni sono enormemente potenti. Riuscire a ricavare dei risultati su un caso particolare della realtà significa che quei risultati funzioneranno solo ed esclusivamente per quel caso particolare; ricavare dei risultati su un’astrazione significa che quei risultati varranno per tutti i casi particolari di quell’astrazione, che potrebbero anche essere molti. Tutto ciò che sappiamo sui computer può essere applicato a qualsiasi cosa possiamo etichettare come "bit", sia esso un mucchietto di elettroni, la quantità di liquido in un recipiente o, per l’appunto, delle palle da biliardo.
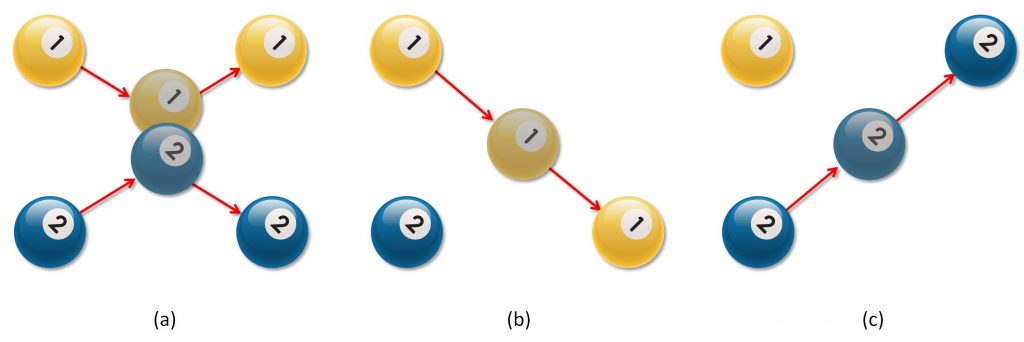
Figura 2: Un computer a palle da biliardo
Abbiamo le nostre due belle palle da biliardo su un lato del tavolo, e possiamo decidere se lanciarne una, nessuna, o entrambe. Supponiamo di lanciarle entrambe e di essere decentemente in grado di giocare: le due palle si urteranno da qualche parte nel mezzo, e il nostro tiro sarà stato così bello e perfetto che saranno tornate nella stessa posizione di partenza, solo un pò più avanti (Figura 2a). Supponiamo di lanciarne una soltanto. Non ci sono urti all’orizzonte, quindi la palla filerà dritta per la sua strada e si fermerà in corrispondenza di quell’altra (Figura 2b e c), solo un pò più avanti (sì, siamo davvero bravi a questo gioco). Se non ne lanciamo nessuna, ovviamente dall’altra parte non troveremo nulla.
Che conclusione possiamo trarre da tutto questo, a parte che siamo degli artisti del biliardo? Bè, se ci fate caso, ritroveremo le due palle nella stessa posizione di partenza se e solo se abbiamo eseguito entrambi i lanci. Se vediamo l’azione “lancio la palla” come un 1, e l’azione “non lancio la palla” come uno 0, e in generale il “lancio” come l’ingresso del sistema, abbiamo a tutti gli effetti realizzato una AND! Ritroveremo, invece, una delle due palle in posizione opposta a quella di partenza se e solo se NON è stata lanciata l’altra; se è stata lanciata è nella stessa posizione, se NON è stata lanciata è in quella opposta. La posizione di una singola palla equivale all’opposto dell’azione “lancio la palla” applicata all’altra palla: una NOT!
Altro non ci serve: abbiamo un teorema che ci dice che AND e NOT sono le uniche porte di cui abbiamo effettivamente bisogno per realizzare tutte le altre. Dunque, combinando tante palle da biliardo e inventandoci un modo per trasformare i dati che vogliamo elaborare in colpi di stecca, possiamo realizzare il nostro computer.
C’è tutta una serie di motivi per cui un computer a palle da biliardo non è di grande utilità pratica, ma per il momento concentriamoci sul più ovvio: l’ingombro. In confronto a questo, l’ENIAC è un bruscolino. Ma il punto non è questo; il punto è che le palle da biliardo sono a tutti gli effetti un’alternativa scomoda ai transistor. Ma, come potete facilmente immaginare, non si tratta dell’unica.
IL QUBIT
Spostiamoci sull’altro lato dello spettro: possiamo tirar fuori un bit da un elettrone? Sì? No? Ne vale effettivamente la pena?
Bè, per avere un bit ci servono due caratteristiche dell’elettrone cui associare le etichette “0” e “1”. Se non vi ho perso dalle parti del tavolo da biliardo, a questo punto dovrebbe essere chiaro che una cosa vale l’altra, basta che poi siamo in grado di lavorarci nel mondo reale, e di costruirci un vero dispositivo. La grandezza che spesso e volentieri si considera è lo spin. Probabilmente qualcuno di voi ne avrà sentito parlare, e se vi chiedessi cos’è lo spin probabilmente mi rispondereste che è il verso di rotazione dell’elettrone. Un elettrone può ruotare solo in due modi, a destra e a sinistra. E’ una definizione molto diffusa, ma è anche una grandissima fesseria. Se vi sedeste e faceste un pò di conti con l’ipotesi di elettrone che ruota, arrivereste a contraddizioni fisiche.
Rispondere alla domanda “cos’è lo spin” è più o meno lo stesso che rispondere alla domanda “cos’è la carica elettrica”. Cos’è la carica elettrica? Un “più” o un “meno” disegnati sopra ad una particella? La carica elettrica è quel qualcosa, quella proprietà magica, che certe particelle hanno e che fa sì che si comportino in un certo modo se immerse in un campo elettrico. Allo stesso modo, lo spin è quella proprietà magica degli elettroni che fa sì che si comportino in un certo modo se immersi in un campo magnetico. Prendete un grosso magnete, mettetelo davanti ad uno schermo in grado di rilevare l’impatto degli elettroni e sparatene un fascio lì nel mezzo. Osserverete che metà degli elettroni finirà al di sopra della direzione di propagazione del fascio e metà al di sotto, come nella Figura 3. Si dice che gli elettroni che sono andati di sopra hanno spin “up”, e quelli che sono andati di sotto hanno spin “down”.
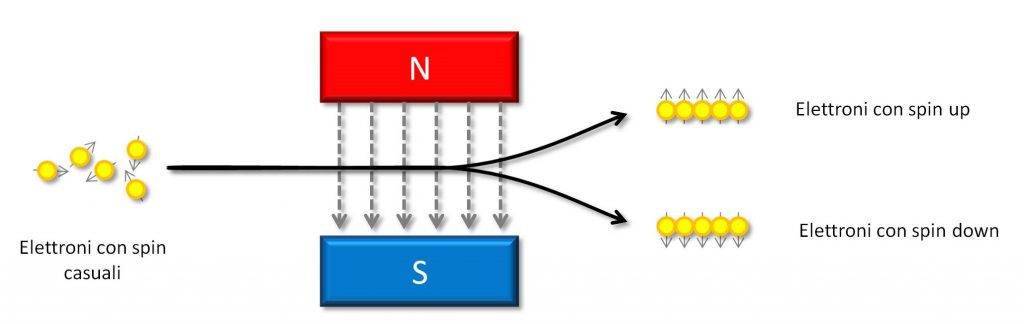
Figura 3: Elettroni in un campo magnetico
Lo spin, quindi, qualunque cosa esso sia, sembra fare al caso nostro. Gli elettroni hanno solo due valori di spin, cioè hanno solo due possibili comportamenti se immersi in un campo magnetico, che possiamo facilmente distinguere. Possiamo tranquillamente dire che, se l’elettrone ha spin up, abbiamo un “1”, e che se l’elettrone ha spin down, abbiamo uno “0”. Potete fare anche il contrario, se preferite, non cambia nulla.
Fin qui tutto bene. Ora, i problemi (ma anche le opportunità) compaiono se facciamo una cosa che spesso è pericoloso fare: se ci chiediamo perché. Perché gli elettroni sparati attraverso il campo magnetico si dividono equamente in due mucchietti? E perché proprio e soltanto due? Bè, il fatto che siano due è un’altra delle cose che capitano spesso quando si ha a che fare con le particelle elementari, cioè che, in molti casi, certe grandezze sono quantizzate, ovvero possono assumere solo particolari valori. Non abbiamo una risposta al perché sia così; è ciò che si osserva. La natura funziona così, punto. Gli elettroni hanno solo due comportamenti possibili, se immersi in un campo magnetico. Se gli elettroni avessero avuto tre comportamenti possibili, avremmo osservato tre mucchietti.
Perché questa divisione sia equa, cioè perché metà degli elettroni vada di sopra e metà di sotto, invece, è tutto un altro discorso. Potremmo pensare che sia un problema dell’apparato con il quale abbiamo preparato gli elettroni. Magari non si tratta di un apparato molto preciso, anzi, è così impreciso che statisticamente prepara metà degli elettroni con spin up e metà con spin down.
Bene. Consideriamo un altro esperimento. Prendiamo un elettrone. Uno soltanto. Il nostro apparato fa schifo, quindi abbiamo un 50 % di probabilità che ce lo abbia prodotto con spin up, e un 50 % con spin down. Diciamo che, dopo il passaggio attraverso il magnete, scopriamo che ha spin up. Bene. Mettiamo ora un altro magnete dopo il primo. L’elettrone che vi entra ha spin up, quindi ci aspettiamo che continui ad andare di sopra, giusto? Invece no. Metà delle volte andrà di sopra, e metà andrà di sotto. È ciò che si osserva.
Che conclusioni possiamo trarre da tutto questo? Almeno due. Uno, che la meccanica quantistica è strana. Due, che la probabilità del 50 % di avere spin up non è un problema dell’apparato che ha prodotto l’elettrone, ma una sua caratteristica intrinseca. Di suo, l’elettrone non si trova in uno stato ben preciso, ma contemporaneamente in entrambi. A priori non possiamo sapere in quale, ma possiamo scoprirlo solo dopo aver misurato, dopo essere andati a guardare. I fisici dicono che l’elettrone si trova nella sovrapposizione dei due stati.

Figura 4: Un tipico gatto di Schrodinger
ATTENZIONE: quello che hai appena letto è solo un estratto, l'Articolo Tecnico completo è composto da ben 2945 parole ed è riservato agli ABBONATI. Con l'Abbonamento avrai anche accesso a tutti gli altri Articoli Tecnici che potrai leggere in formato PDF per un anno. ABBONATI ORA, è semplice e sicuro.