Dentro un Computer Quantistico: la misteriosa azione a distanza

Si sente spesso dire che la meccanica quantistica è difficile perché prevede tutta una serie di fenomeni che nel mondo “reale” (e qui per “reale” intendo quello fatto di cose che possiamo vedere e toccare) non hanno un equivalente. Uno di questi fenomeni è l’effetto tunnel, che ci presenta una particella che fa cose che l’equivalente “reale”, tipo una palla da biliardo, non potrebbe fare. Un altro, quello di cui vi parleremo oggi, ha invece a che fare con ciò che riescono a combinare due particelle accoppiate in modo particolare. Se nella lettura di ciò che seguirà vi verrà voglia di grattarvi perplessi la testa, non sentitevi sminuiti. Del resto, ha creato qualche difficoltà anche allo stesso Albert Einstein.

AI CONFINI DELLA REALTA’

E a proposito del non sentirsi sminuiti, vorrei puntualizzare il fatto che questo essere controintuitivo della meccanica quantistica in fin dei conti non è molto intuitivo. Nel senso: spesso, nonostante questi fenomeni, nella testa del fisico scafato che ve li sta raccontando siano assurdi, la reazione tipica che suscitano è un profano “sì, e quindi?”

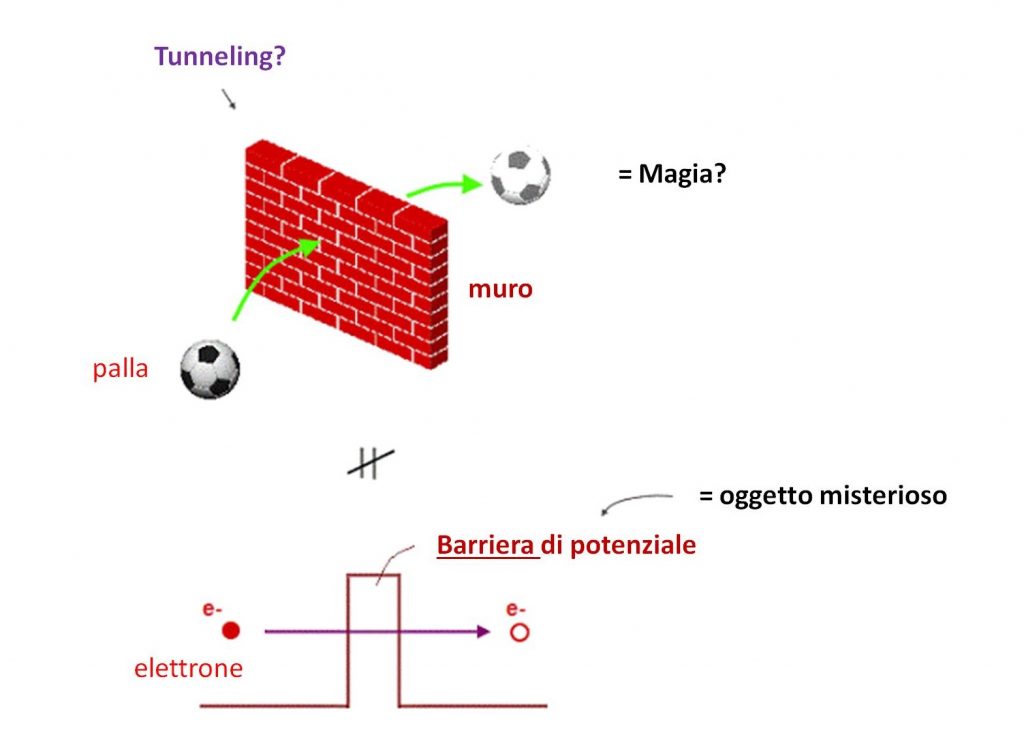
Figura 1: L'effetto tunnel

Prendiamo per esempio l’effetto tunnel. Quando mi venne detto per la prima volta che il succo dell’effetto tunnel è che una particella con una certa energia, posta di fronte ad una barriera di potenziale di una certa altezza, ha una probabilità non nulla di passare dall’altra parte, ricordo di essermi grattato la testa e aver pensato: “sì, e quindi?” Una barriera di potenziale non è una cosa facile da visualizzare. Così bisogna fare l’esempio nel mondo reale e dire che equivale al sapere che c’è una persona in una stanza buia divisa in due da un muro, di sapere che questa persona è stata messa da un lato del muro, e che se si accende la luce per verificare che effettivamente la persona si trova lì dove l’abbiamo messa, potrebbe capitare qualche volta di ritrovarla dall’altro lato. E se te la mettono così, allora la cosa sembra davvero assurda. Con l’entanglement la situazione è simile. Il fisico scafato ci dice che, se due particelle si trovano in uno stato entangled, allora la misura effettuata su una delle due determina lo stato della seconda, istantaneamente e indipendentemente dalla distanza reciproca delle due.

Sì, e quindi?

Quindi questo viola tutta una serie di leggi fisiche. Una particella elementare non si può sapere chi è o che sta facendo fino a che non la si misura. Dire che la misura su una ha effetto sullo stato dell’altra equivale a dire che, nel momento in cui vado a controllare il mio qubit e lo trovo a zero, chiunque dovesse andare a controllare l’altro qubit, che potrebbe trovarsi tanto nella stanza accanto quanto all’altro capo dell’universo, necessariamente lo troverà (ad esempio) ad uno. Questo, a sua volta, significa che sono riuscito a trasmettere istantaneamente un bit di informazione all’altro capo dell’universo. E fin qui non ci sarebbe nulla di strano se non fosse per quell’istantaneamente. L’informazione viaggia al più su onde elettromagnetiche, siano esse impulsi laser, segnali radio o chi per loro, e le onde elettromagnetiche non possono viaggiare a velocità maggiori di quella della luce. Dunque, quell’istantaneamente ci dice che abbiamo trasmesso informazione a velocità maggiori di quella della luce. In pratica, che abbiamo violato la relatività ristretta.

Non c’è da stupirsi se ad Einstein questa cosa non piacesse.

DUE CONTI (ANCHE PER I DEBOLI DI CUORE)

Il problema è che l’entanglement e questa “misteriosa azione a distanza” (cit.) saltano fuori in maniera abbastanza naturale quando si considerano sistemi a due particelle. Dal punto di vista della notazione, se:

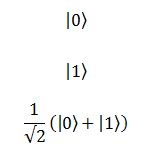
rappresentano rispettivamente una particella che sappiamo per certo ha spin up, una che di sicuro ha spin down, e una che la metà delle volte che l’andiamo a controllare ha spin up e l’altra metà down, allora:

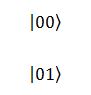
rappresentano rispettivamente un sistema di due particelle in cui le due hanno sempre spin up e uno in cui la prima ha sempre spin up e la seconda sempre spin down. (Nota: L’associazione bit a zero = spin up e bit a uno = spin down è perfettamente arbitraria; avremmo potuto fare tranquillamente il contrario, come pure usare gli spin destra/sinistra o avanti/dietro). Questi due esempi rappresentano stati di sistemi a due particelle in cui abbiamo eseguito delle misure (non dimentichiamocelo mai, in meccanica quantistica misurare è l’unico modo per conoscere esattamente lo stato di una particella), ma possiamo avere anche stati in cui le particelle sono entrambe in sovrapposizione. Senza scendere troppo nel dettaglio del perché si possa scrivere così, questo caso lo possiamo scrivere così:

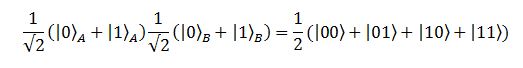
In questa notazione, i pedici “A” e “B” vengono usati per distinguere la prima particella dalla seconda qualora non si capisse; una volta esplicitati i conti, invece, si dà per scontato che il primo 0 o 1 nel ket sia riferito alla prima particella e il secondo alla seconda. Questo stato ci permette di dire un pò di cose interessanti. La prima è che esso contiene, allo stesso tempo, tutte e quattro le possibili combinazioni che possiamo formare con due bit, il che equivale a dire che le due particelle sono contemporaneamente in questi quattro stati. È il concetto di sovrapposizione che ci permette di eseguire calcoli molto più rapidamente di quanto non sarebbe possibile in un computer “normale”. La seconda cosa è il numero di fronte allo stato. Quel numero, elevato al quadrato, ci dice la probabilità di ottenere la parte della sovrapposizione che moltiplica, nel caso andassimo ad eseguire la misura. Così, ad esempio, nello stato:

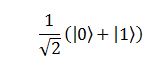
entrambi i bit hanno il 50 % (1/2) di probabilità di saltare fuori, mentre nello stato:

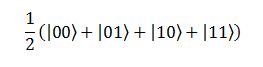
tutte e quattro le combinazioni hanno il 25% (1/4, ossia 1/2 al quadrato) di probabilità di essere misurate.

La terza cosa viene da ciò che accade quando eseguiamo delle misure. Supponiamo di misurare la prima particella, perché vogliamo sapere se è zero o uno. Sappiamo che la metà delle volte troveremo 0 e l’altra metà 1. Diciamo che questa volta venga zero. Che dire dell’altra particella? In che stato sarà? A intuito potremmo dire che non ne abbiamo idea, perché mai la misura sulla prima particella dovrebbe avere effetto sulla seconda? In effetti, osservando l’espressione dello stato, notiamo che se la prima particella ha spin up (0), la seconda può avere tanto spin up quanto spin down (0 o 1), e lo stesso se la prima ha spin down, ma non abbiamo modo di dire che sta facendo la seconda senza eseguire una seconda misura su di essa. E a rigore possiamo anche dimostrare che le cose stanno così, non è difficile. Ricordiamo che “misurare”, in questo contesto equivale a calcolare il prodotto scalare con il vettore della base lungo cui misuriamo, cosa che, nella notazione di Dirac, si traduce nel calcolare:

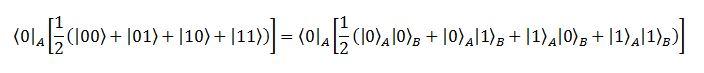
Abbiamo rimesso dentro i pedici per evitare confusione, perché non si può calcolare la proiezione della prima particella sulla seconda, che senso avrebbe? Sorvolando sulle costanti, da questo calcolo rimane:

Il motivo è che:

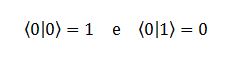
Questo è ovvio, dal momento che il primo caso equivale a chiedere “quanto spin up abbiamo se lo stato è spin up”, ed è ovviamente 1, mentre il secondo a chiedere “quanto spin up abbiamo se lo stato è spin down”, che è ovviamente 0. Quindi, i due pezzi che rimangono sono solo i due relativi alla seconda particella, e in parti uguali, per giunta. Dunque, tutto questo ci dice che, se misuriamo la prima particella e la troviamo a zero, la seconda starà beatamente in sovrapposizione, ignara di ciò che è successo alla prima.

QUATTRO CONTI IN PIU’

Fin qui tutto ok, è ciò che ci saremmo aspettati. Se lanciamo in aria due monete, entrambe cadranno su testa o croce indipendentemente l’una dall’altra. Consideriamo però uno stato di questo tipo:

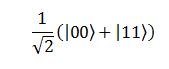
Si tratta di uno stato legittimo? Bè, sì, perché no? Un sistema a due particelle lo possiamo vedere come uno spazio vettoriale a quattro dimensioni, in cui i vettori della base sono le quattro combinazioni possibili di zero e uno; i quattro che formavano la sovrapposizione perfetta di prima. Dunque, tutte le possibili combinazioni lineari di quei quattro vettori sono state permesse, e il generico stato sarà del tipo:

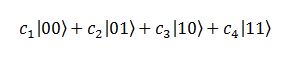
Mettendo a zero c₂ e c₃ otteniamo lo stato di sopra – è un pò come prendere un punto sul piano xy del comune spazio 3D, mettendo a zero la z. Dunque, se si tratta di uno stato (matematicamente) legittimo, allora possono esistere due particelle in esso. Che stanno facendo queste particelle? La formula ci dice che si tratta di uno stato in cui, se si va a misurare, metà delle volte (il quadrato di 1/√2) si troverà la prima con spin up e la seconda anche, e l’altra metà delle volte la prima con spin down e la seconda anche. Questa piccola, insignificante ‘e’ congiunzione è l’origine di tutti i mali. Perché, qui la misura sulla prima particella non produce ambiguità: se la prima è 0, anche la seconda lo deve essere, e se la prima è uno, anche la seconda lo deve essere. In pratica, una misura sulla prima determina lo stato della seconda (e viceversa)! Gli stati delle due particelle sono intrecciati, entangled per l’appunto, e si influenzano a vicenda. E considerate anche che qui nello stato compare solo ed esclusivamente lo spin, non si fa alcun accenno su velocità, posizione, energia o chi per loro delle particelle. Questo non significa che non le abbiano, ovviamente, le particelle saranno da qualche parte e avranno una qualche energia, solo questi parametri non rientrano nell’equazione. La misura dello spin, come è giusto che sia, non dipende da dove si trova la particella, ma può dipendere da quello di un'altra, se quest’ultima è entangled con la prima. È come dire che, se ci troviamo in una stanza buia in cui sappiamo che c’è un appendiabiti, accendendo la luce e misurando la sua altezza, determiniamo quella di un altro non necessariamente lì vicino, ma magari nel palazzo affianco, nella città dopo o direttamente su un altro pianeta.

Da un punto di vista rigoroso è ancora più semplice da vedere. Basta calcolare:

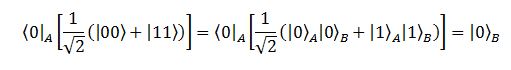
sempre ricordando che:

E di stati di questo tipo, troppi ne possiamo inventare. I più importanti sono i fratelli di quello (s)considerato un attimo fa, gli stati di Bell:

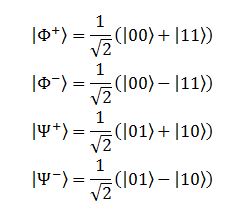
La loro importanza è duplice: uno, si può dimostrare che sono gli stati più correlati (e quindi con entanglement più “forte”, per così dire) che si possano creare; due, sono una base dello spazio vettoriale che descrive lo stato delle due particelle, alternativo a quello “classico” formato dai vettori:

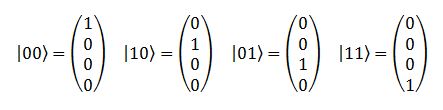
Dire che gli stati di Bell formano una base dello spazio degli stati dei sistemi a due particelle equivale a dire che, quale che sia lo stato delle nostre due particelle, comunque lo potremo descrivere come sovrapposizione di stati di Bell. Dunque, potremo effettuare delle misure lungo gli stati di Bell: questo significa che possiamo rispondere a domande come “quanto c’è nel nostro stato?”, così come chiedere “quanta parte del nostro sistema è fatta da entrambe le particelle con spin up” equivale a misurare lungo. E questo, come vedremo la prossima volta, è fondamentale quando gli stati entangled li si va ad utilizzare. Appurato che questi stati hanno senso (matematico) e sono anche importanti, resta la domanda cruciale: possiamo crearli? Nel senso, esiste qualche circuito quantistico che, presi in ingresso due qubit, restituisce gli stessi qubit ma in uno stato entangled? Perché la matematica è bella e cara, ma se non li si riconduce a qualcosa di più tangibile, con gli stati di Bell non ci facciamo un bel(l) nulla.

[...]

ATTENZIONE: quello che hai appena letto è solo un estratto, l'Articolo Tecnico completo è composto da ben 3045 parole ed è riservato agli ABBONATI. Con l'Abbonamento avrai anche accesso a tutti gli altri Articoli Tecnici che potrai leggere in formato PDF per un anno. ABBONATI ORA, è semplice e sicuro.