
Parlando di rumore, di qualità dell'informazione e di bit corrotti nell'ambito dei sigma delta in una delle puntate del nostro corso di microprgrammazione, abbiamo affrontato due temi fondamentali ovvero la qualità dell'informazione e la profondità di rappresentazione della stessa. Nacque l'esigenza di
approfondire algoritmi specifici come l'UV-22 ed i nostri lettori sono stati accontentati. Ma dal momento che l'argomento è tutt'altro che esaurito, oggi torniamo ad approfondire il dithering, probabilmente uno dei concetti più ostici ma più fondamentali riguardo l'audio digitale. Buona lettura.
Quando si parla di digitalizzazione di un segnale c'è bisogno di particolari e di approfondimento perché i problemi sono potenzialmente tantissimi, la codifica è un fatto cruciale ma soprattutto la qualità dell'informazione non è garantita a prescindere ma deve essere preservata rispetto a sorgenti di rumore sistematiche piuttosto che casuali.
Il concetto di dithering non è particolarmente intuitivo perché a primo impatto l'idea di aggiungere del rumore per poter avere un segnale meno rumoroso non ha alcun senso.
Storicamente, però, può essere contestualizzato nell'epoca precedente la seconda guerra mondiale, quando la flotta inglese stava sperimentando problemi con i sistemi di navigazione. Sembrava che il problema fossero i movimenti grossolani degli ingranaggi a rendere impossibile la calibrazione. Questi stessi problemi, però, sembravano non esserci durante il volo. Sembrò che le vibrazioni dei motori avessero un qualche effetto "lubrificante" che rendeva tutto funzionale.
Aggiungere rumore in questo modo ha, paradossalmente, aumentato la precisione dell'intero sistema. Sapendo che questa poteva essere una soluzione, gli inglesi installarono dei piccoli motori sui loro sistemi di navigazione solamente per introdurre quelle vibrazioni che servivano a far funzionare meglio il tutto.
L'audio
Dither può essere tradotto in italiano con il verbo "agitarsi"; questo rende più facile capire la ragione specifica della tecnica. Ma fino a questo momento abbiamo parlato di segnali digitali abbiamo detto che l'applicazione prevalentemente riguarda l'audio. Quindi, in che modo?
Quando si parla di audio cerchiamo sempre di evitare forme di troncamento che rendano il segnale poco "fluido" e d'altronde è ovvio perché quando cambiamo la risoluzione del segnale ovvero la profondità di rappresentazione incorriamo nell'errore di quantizzazione. Questa componente c'è sempre, evidentemente ed il nostro scopo è sempre quello di cercare di minimizzarlo.
Possiamo provare a visualizzare una sinusoide alla frequenza di 100 Hz rappresentata con 24 bit:
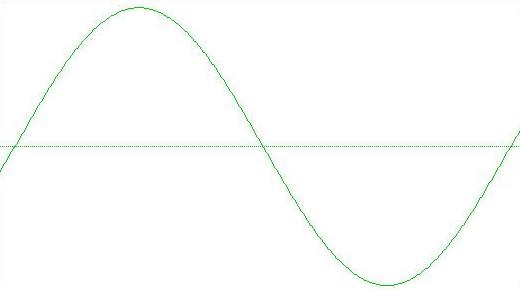
ecco come visualizzeremo, invece, la stessa senza una rappresentazione così "profonda". Passiamo a 16 bit:
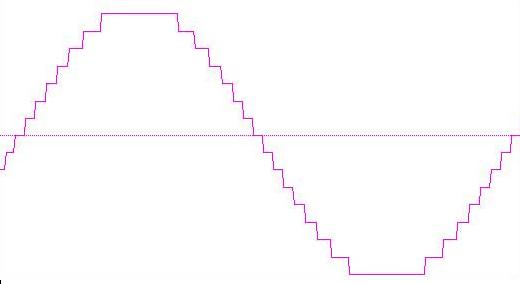
La differenza qualitativa è chiara: i passi di quantizzazione sono evidenti, il segnale si presenta "a gradoni" e noi possiamo immaginare sia una sinusoide pensando di approssimare il tutto ad una curva che attraversa i fronti di salita e di discesa.
La forma a gradino di ciascuno dei "salti" non è soltanto un fatto estetico ma a un vero e proprio effetto udibile. Quello che vediamo può essere trasformato, naturalmente tramite Fourier, generando una distorsione armonica.
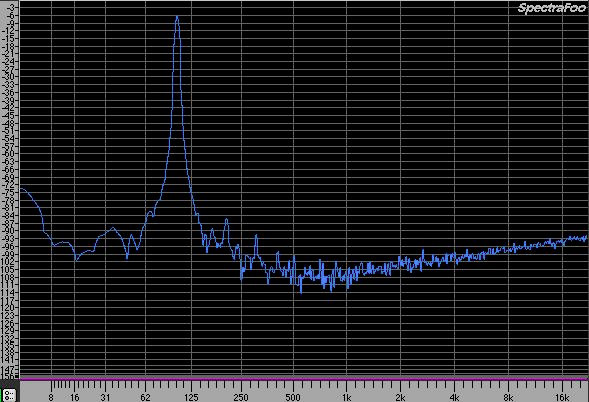
Nell'immagine appena vista, lo spettro del segnale rappresentato con 24 bit.
Nella figura che segue invece, vediamo la stessa però del segnale a 16 bit:
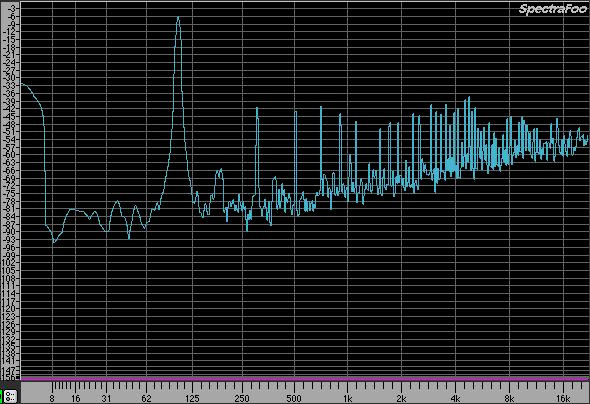
Sia nel tempo sia nelle frequenze, com'è ovvio, la profondità di rappresentazione ha degli effetti che affliggono ed inficiano la qualità della visualizzazione. Non è, ancora una volta, solo un fatto estetico perché più il segnale è definito migliore sarà il trattamento che un sistema generico riuscirà a riservare al segnale.
Quando la rappresentazione è a 24 bit il livello di rumore è ben più basso, circa 50 dB; questo dipende dal fatto che il cosiddetto dynamic range tra i 16 ed i 24 bit è proprio di 48 dB.
Giochiamo al caso
Non è ancora chiaro per quale motivo introdurre una componente aleatoria sul segnale audio. Soprattutto perché aggiungeremmo del rumore casuale che potrebbe rovinare, dal punto di vista statistico, la caratterizzazione del segnale.
Il rumore viene creato selezionando valori a caso per i bit. Tra 16 e 24 bit ce ne sono 8; supponiamo di aggiungerne 9 di rumore, ovvero di aggiungere al valore del segnale un numero compreso fra 0 e 512 (ovvero tra -256 e 256).
Questa serie di numeri crea del rumore bianco aggiunto al segnale.
Provate ad immaginare di tirare un dado: la probabilità che esca una delle facce è equivalente (se il dado è onesto!). Quindi su sei facce sappiamo che la probabilità è 1/6, una distribuzione uniforme ma sappiamo anche che le facce indicano valori discreti per cui sarà discreta. La distribuzione uniforme è la più semplice alla quale possiamo pensare ma già lanciare due dadi restituisce una distribuzione diversa.
Parleremo prevalentemente di quella triangolare e c'è un motivo perché per noi è la sorgente di rumore, visto che stiamo cercando di ottenere un determinato effetto piuttosto che utilizzare il rumore bianco. Immaginate di avere a disposizione un segnale continuo che si trovi esattamente a metà tra due passi di quantizzazione contigui. Dal momento che noi vogliamo che ci sia la stessa probabilità di finire a quantizzare il segnale con livello più basso e con livello più alto, se il segnale stesso è soltanto al 20% di distanza da uno dei due passi di quantizzazione quello che vogliamo è avere un numero di passi di quantizzazione proporzionato per attribuire il valore corretto.
Stiamo dicendo che lavoreremo con un algoritmo che ci permetta di definire precisamente il risultato, più accurato, che possiamo raggiungere dal punto di vista statistico.
Una volta filtrati e convertiti da un convertitore D/A, i risultati saranno sicuramente soddisfacenti.
Sì, ma come?
Il rumore bianco è un fenomeno statistico derivato dalla fluttuazione disordinata dei portatori. La sua media statistica è sicuramente nulla ed infatti la sua densità di potenza è continua.
Quello che generiamo non è davvero rumore né bianco né triangolare né di nessun tipo ma si tratta della migliore approssimazione che possiamo ottenere dal momento che la precisione di rappresentazione che possiamo sfruttare è finita, 32 o 64 bit. Un numero reale però può essere rappresentato con una precisione infinita, con un numero di cifre decimali infinito e questo, ovviamente, non è simulabile.
Che effetto ha? Semplice: non avremo mai a che fare con rumore "vero".
È un problema? A rigore diremmo "dipende". Nella pratica, possiamo lavorare tranquillamente con segnali la cui approssimazione sia a 32 bit, dal momento che stiamo pur sempre parlando di segnali che vengono elaborati dal computer.
Abbiamo, allora, a che fare con parole da 24 bit ma gli ultimi, quelli meno significativi, hanno valori casuali; se li togliamo è facile intuire cosa verrà fuori: avremo lo stesso segnale troncato
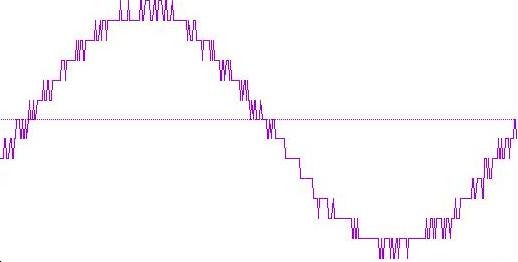
Qui sono evidenti non soltanto i valori del segnale, perché altrimenti avremmo di nuovo i "gradoni" di prima ma le fluttuazioni statistiche del segnale relative alla precisione di rappresentazione.
E se facciamo l'analisi spettrale di questo segnale? Una distorsione armonica; adesso abbiamo rumore bianco, almeno di fondo, più alto rispetto all'originale ma questa volta abbiamo un vero plafond di rumore bianco e quindi non abbiamo più distorsioni simili alle precedenti. Vediamolo con una figura
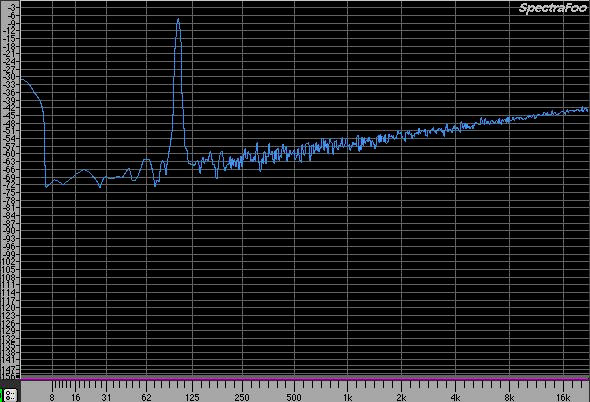
Si vede la differenza? Se facciamo un paragone tra questo segnale e l'originale troncato noteremo che il secondo ha un livello di fondo di rumore sicuramente più basso per alcune frequenze ma la componente di rumore di picco è di gran lunga più alta rispetto alla versione dithered.
Il nuovo segnale va un livello di rumorosità più basso e non restituisce le stesse distorsioni di quelle relative all'onda quadra. Ecco perché ci troviamo meglio e abbiamo una sensazione completamente diversa.
Ciò va argomentato dal punto di vista spettrale ed è per questo che vediamo la figura che segue
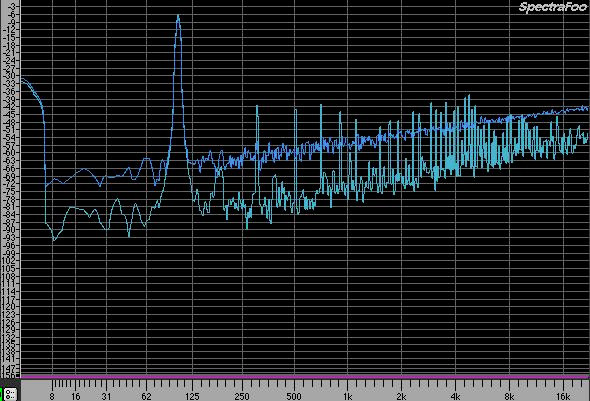
in cui queste differenze sono palesi.
Se il segnale viene dimezzato il risoluzione, da 96 a 48 bit, per esempio, questo processo è indispensabile e lo è ancora di più se il numero di bit di partenza è più basso.
Il processo di conversione analogica implica già di per sé il Dithering perché il rumore termico nel convertitore "lavora" già quando si effettua il troncamento e l'approssimazione, e gli effetti si sovrappongono.
Fin qui tutto bene
Il fenomeno è tutto sommato abbastanza semplice e basta prenderci confidenza per comprenderlo al meglio. Ma non è tutto. La discussione può essere più complicata se cominciammo a ragionare sugli algoritmi utilizzati da applicazioni particolari.
Qui l'idea di base è che si potrebbe aggiungere rumore oltre al rumore bianco che potremmo definire meno fastidioso all'orecchio umano (ricordiamoci che stiamo sempre parlando di applicazioni audio!).
Come sappiamo, l'orecchio umano non è ugualmente sensibile a tutte le frequenze. Ecco perché sono stati sviluppati diversi algoritmi che lavorano su questo fenomeno ed uno di questi è proprio l'UV-22.
Vi siete chiesti perché 22? O forse l'avevate capito già da l'altra volta? 22 è una frequenza, sono kHz. Rappresenta il valore che rispetta il teorema di Nyquist. Per completezza vi facciamo vedere il solo rumore aggiunto con l'algoritmo UV-22

e di seguito il suo spettro
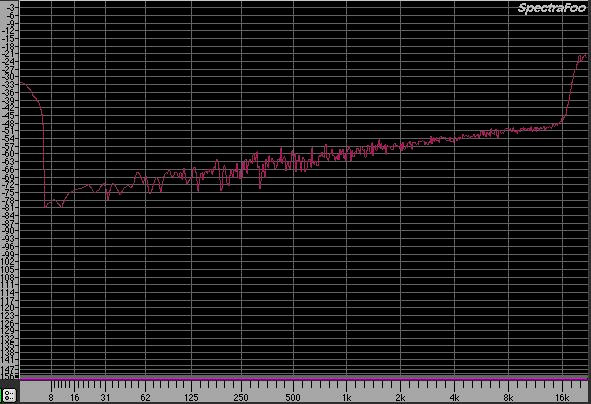
Si vede, in maniera anche abbastanza chiara, che non soltanto il rumore assomiglia ad una densità triangolare, dal momento che la maggior parte dei punti si trovano attorno all'attraversamento per lo zero, ma è filtrato.
Si può anche osservare che il picco di questo rumore è più alto di quello precedente ma l'ampiezza è raggiunta solo a frequenze più alte.
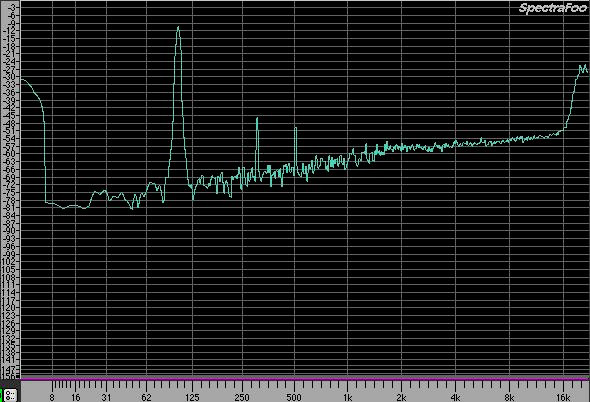
Nello spettro si vede chiaramente che l'aumento dell'energia avviene soltanto intorno ai 16 kHz, dove, per l'appunto, essa è concentrata.
Sebbene siano possibili degli artefatti, il rumore aggiunto alla sinusoide viene, a restituire uno spettro del tipo
Conclusioni
Speriamo di avervi chiarito le idee sul metodo con cui è possibile da un lato ingannare l'orecchio, dall'altro sfruttare le sue caratteristiche ma soprattutto lavorare con il rumore piuttosto che considerarlo una componente dannosa. La sua presenza è inevitabile per cui tanto vale farci i conti e, se possibile, gestirlo in maniera ottimale.
E così, abbiamo scoperto che aggiungere rumore può creare ottimi risultati sugli artefatti, ridurre problemi di quantizzazione, del troncamento e della profondità di rappresentazione del segnale.
Esistono evoluzioni di questa tecnica, ovvero il dithering "colorato": come il nome suggerisce, non si tratta più di aggiungere rumore bianco ma di un processo da applicare utilizzando rumore solo per alcune componenti spettrali. Se è nella sua versione colorata, il Dithering deve essere l'ultimo passaggio di elaborazione dell'audio, pena avere terribili risultati.
Ed ora, la parola a voi: che esperienze avete con questa tecnica?






ci tengo a farvi i complimenti, avete approfondito benissimo e sono molto interessanti gli algoritmi contenuti nel link indicato.
per rispondere alla domanda finale non ho esperienza diretta e di solito ascolto più che creare musica però mi avete fatto venire voglia di provare a fare qualche elaborazione.vi terrò informati.