Il firmware descritto, abbinato ad un microcontrollore PIC, consente di effettuare la misura del vero valore efficace e del livello in dB di un qualunque segnale analogico.
Il valore efficace di una grandezza elettrica in corrente alternata è un parametro che ha lo scopo di semplificare i calcoli ingegneristici (al seguente link un approfondimento sugli errori sperimentali) evitando di analizzare ogni istante infinitesimo che costituisce la forma d’onda. Il valore efficace di una grandezza equivale a quel valore che in regime di tensione continua svilupperebbe la stessa potenza. Un segnale variabile periodico infatti non ha un valore definito di tensione o corrente come nel caso della corrente continua, ma varia istante per istante. Ad esempio sottoponendo un resistore a una corrente alternata di 34 Vpp (cioè di forma d’onda sinusoidale variabile in ampiezza fra +17 e -17 V) si svilupperebbero gli stessi effetti di riscaldamento come se fosse sottoposto a una tensione continua di 12 V. La formula seguente consente di calcolare il valore efficace o RMS (Root Mean Square) di una qualsiasi funzione, data una serie di N valori:
Tale espressione si semplifica nel caso di un segnale sinusoidale:
Molti strumenti di misura, tra cui i multimetri più economici, sono calibrati per mostrare il valore efficace in funzione del valore medio di una tensione sinusoidale raddrizzata. Il metodo funziona bene se il segnale ha forma d’onda perfettamente sinusoidale, ma dà risultati completamente errati se il segnale è distorto oppure ha una forma d’onda non sinusoidale o presenta una corrente continua sovrapposta. L’errore aumenta con l’aumentare della ricchezza in armoniche del segnale. Alcuni strumenti sono in grado di operare il calcolo del vero valore efficace, campionando il segnale ed eseguendo i calcoli in tempo reale. Questi apparecchi sono contraddistinti dalla sigla true RMS. La realizzazione di uno strumento a vero valore efficace è notevolmente semplificata utilizzando un microcontrollore. Nel Listato 1 è riportato il codice da utilizzare per il calcolo e la visualizzazione del valore efficace di una tensione in ingresso sul pin A1. Inoltre, lo stesso codice effettua anche il calcolo dello stesso valore espresso in dB. L’intero firmware è basato sull’uso del convertitore A/D in ingresso al PIC. Esso effettua il campionamento di N valori (nella fattispecie 3000) della forma d’onda; le righe di codice da 26 a 29 effettuano la sommatoria dei valori quadrati della funzione campionata
Utilizzando un PIC alimentato a 5V sarà necessario precondizionare il segnale analogico, facendo in modo che le sue variazioni siano comprese tra 0V e 5V. Valori esterni a questo intervallo pregiudicherebbero la correttezza della misura. Come si nota la riga di codice 30 esegue una divisione che a prima vista potrebbe sembrare strana, se non addirittura sbagliata. In realtà tale operazione è necessaria poiché i valori acquisiti con l’ADC del PIC sono unità comprese tra 0 e 255, ma in realtà non esprimono il valore in volt della forma d’onda. Quindi sarà necessario considerare un fattore correttivo che ne tenga conto, secondo la formula seguente: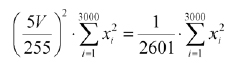
A questo punto non resta che effettuare la divisone per il numero dei campioni (3000) e la radice quadrata del risultato. Il calcolo del valore efficace espresso in dB è molto semplice ed è eseguito tramite la seguente formula:
I risultati così ottenuti sono visualizzati tramite porta seriale su di un PC. Ovviamente, utilizzando come visualizzazione un display LCD, per esempio, è facile costruire uno strumento RMS portatile.
// Compilatore: CCS
#if defined(__PCM__)
#include <16F877.h>
#fuses HS,NOWDT,NOPROTECT,NOLVP
#use delay(clock=20000000)
#use rs232(baud=9600, xmit=PIN_C6, rcv=PIN_C7)
#elif defined(__PCH__)
#include <18F452.h>
#fuses HS,NOWDT,NOPROTECT,NOLVP
#use delay(clock=20000000)
#use rs232(baud=9600, xmit=PIN_C6, rcv=PIN_C7)
#endif
#include <math.h>
void main() {
const long NUM_DATA_POINTS = 3000;
long i;
int value;
float voltage;
printf(“Calcolando…:\r\n”);
setup_port_a( ALL_ANALOG );
setup_adc( ADC_CLOCK_INTERNAL );
set_adc_channel( 1 );
while(TRUE)
{
voltage = 0;
for(i=0; i<NUM_DATA_POINTS; ++i){
value = Read_ADC();
voltage += (float)value*(float)value;
}
voltage /=2601.0;
voltage = sqrt(voltage/(NUM_DATA_POINTS));
printf(“\r\nInput = %f V %f dB\r\n”, voltage, 20*log10(voltage));
}
| Listato 1 |
In generare il valore efficace semplifica i conti ingegneristici, il calcolo viene fatto partendo dal valor medio del segnale oppure utilizzando anche dei convertitori a vero valore efficace.
È possibile eseguire un test? Ad esempio, ho provato a calcolare analiticamente il valor medio e il valore efficace di un segnale analogico che simula il processo di carica di un condensatore + quello di scarica:
http://tinyurl.com/condensatore
Ottimo esempio di pura matematica applicata all’elettronica. Un piccolo refuso quando scrivi per la prima volta J1, manca l’apice 2 al 10 (pero’ poi l’hai scritto correttamente). Non mi torna il coefficiente davanti (I3+I4)…
ho corretto il refuso. per quanto riguarda quel coefficienti, avevo già controllato con Mathematica… Cmq sto provando con un campionamento discreto. Per ora ho scelto i punti random. in pratica si tratta di calcolare le somme di riemann della funzione y(t)^2, qui il file con il codice mathematica http://extrabyte.info/valore_efficace.pdf
secondo me il coefficiente davanti (I3+I4) è 2*10^3 e non 2*10^-3….forse
ok, più tardi controllo. Nel frattempo mi sono posto la domanda: esistono forme d’onda per le quali il valore efficace coincide con il valore medio? Guardando le formule vediamo che solo il segnale nullo e i segnali costanti verificano questa proprietà, che sembra appunto molto ragionevole per tale classe di segnali. Tuttavia, ho visto che in realtà ciò è una conseguenza di un teorema di analisi funzionale noto come “disuguaglianza di Schwartz”: http://extrabyte.info/valore_eff001.pdf
E’ interessante. Dovrebbero essere solo quelli costanti. Si potrebbe implementare con qualche tool software.
si, solo per i segnali costanti il valor medio coincide con il valore efficace, che è poi è il valore del segnale (dato che è costante). Questo si vede subito dalla formula che definisce il valore efficace, visto che compare il quadrato del segnale. Con la disuguaglianza di Schwartz forse il problema diventa troppo astratto, però è interessante poichè qui l’insieme di tutti i possibili segnali periodici di periodo T compongono uno spazio vettoriale infinito-dimensionale. In pratica ogni segnale y(t) viene interpretato come un vettore a infinite componenti: infatti il valore assunto in t è una componente, al variare di t in [0,T] vengono “spazzate” tutte le componenti e queste sono infinite. A questo punto si procede come nello spazio euclideo, cioè si introduce un prodotto scalare tra i vettori. Precisamente, il prodotto scalare tra due segnali x(t) e y(t) è dato dall’integrale definito tra 0 e T del prodotto x(t)*y(t). Ed è chiaro allora che il valore efficace è proporzionale al quadrato della lunghezza di y(t). Imporre che il valore efficace sia uguale al valore medio, equivale allora ad imporre che y(t) sia o il vettore nullo o un vettore costante.
Marcello, credo tu abbia preso una via troppo astratta,lascia stare gli spazi di Riemann o le funzioni analitiche come pure la disuguaglianza di Schwartz, pensa solo in termini di energia o potenza media, il valore efficace alla fine e’ la media della potenza istantanea sotto radice, ovvero la tensione in continua che da lo stesso valore di energia nel tempo considerato come se fosse alimentata in continua.
Per avere funzioni Reali il cui valore medio e’ uguale al valore efficace dovresti cercare quelle funzioni in cui la primitiva del quadrato e’ identica al quadrato della primitiva della funzione.
Tutte le funzioni periodiche a gradini soddisfano questo requisito,
Il progetto presentato a mio parere non puo’ funzionare o funziona solo per alcune frequenze che siano sottomultiplo della frequenza di campionamento, l’errore con solo 8 bit di risoluzione e’ troppo alto e l’errore e’ inaccettabile per poter essere usato in pratica.
Il periodo di campionamento se non viene sincronizzato alla frequenza del segnale campionato e’ un sottoinsieme del periodo da cui viene a mancare il requisito della definizione di RMS ovvero integrale tra zero e T in cui T e’ il periodo della FDO.
Saluti
Roberto
forse mi sono spinto troppo oltre, ma potrebbe entrarci addirittura la questione della freccia del tempo (in ambito cosmologico). Qui per l’aggiornamento http://tinyurl.com/jqfc6sd (da pag. 2 in poi)