
Seconda parte della serie "Entriamo nei dettagli del DSP o “Digital Signal Processing”" all'interno della Rubrica Firmware Reload di Elettronica Open Source.
I FILTRI DIGITALI NEL BIOMEDICALE
La funzione di un filtro digitale o numerico si può considerare del tutto analoga alla sua controparte analogica. La differenza sta nella sua implementazione: infatti, mentre un filtro analogico viene realizzato utilizzando componenti elettronici passivi e attivi, quello digitale è implementato utilizzando circuiti logici o attraverso un algoritmo software che opera su una sequenza di numeri ottenuta dal campionamento di una forma d’onda continua. In generale, un filtro digitale può essere visto come una procedura numerica o un algoritmo che trasforma una data sequenza di numeri in ingresso in una seconda sequenza in uscita che ha delle proprietà specifiche.
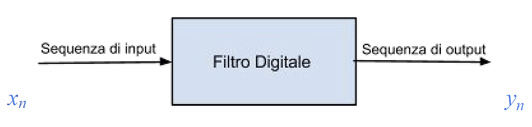
Le proprietà desiderate dipendono ovviamente dall’applicazione. Un esempio classico può essere la riduzione del rumore generato durante l’acquisizione di un segnale proveniente da un determinato sensore. La soppressione del rumore è anche una delle caratteristiche principali quando si parla di filtri in campo biomedicale dato che l’ampiezza dei segnali in gioco quando si acquisiscono segnali di natura biologica come ECG, EMG ed EEG sono nell’intervallo dalle decine alle centinaia di μV. Il filtro digitale presenta numerosi vantaggi rispetto a quello analogico. Una delle caratteristiche più importanti infatti è l’immunità riguardo ai disturbi poiché la sua precisione dipende solo da errori di arrotondamento, essendo determinata dal numero di bit che si utilizza per rappresentare le variabili del filtro stesso. Inoltre, le sue caratteristiche e le sue prestazioni non sono dipendenti da fattori quali l’invecchiamento dei componenti, le variazioni di temperatura e di tensione. Queste peculiarità sono molto importanti soprattutto in applicazioni medicali in cui la maggior parte dei segnali hanno basse frequenze che possono risultare distorte a causa della deriva di un circuito analogico. Le proprietà di un filtro digitale vengono determinate considerando le caratteristiche:
• nel dominio del tempo
- equazioni lineari alle differenze
- filtri a risposta impulsiva
• nel dominio della frequenza
- dominio della trasformata Z (funzione di trasferimento e diagramma poli, zeri)
- dominio della trasformata di Fourier (risposta in frequenza, spettro del segnale)
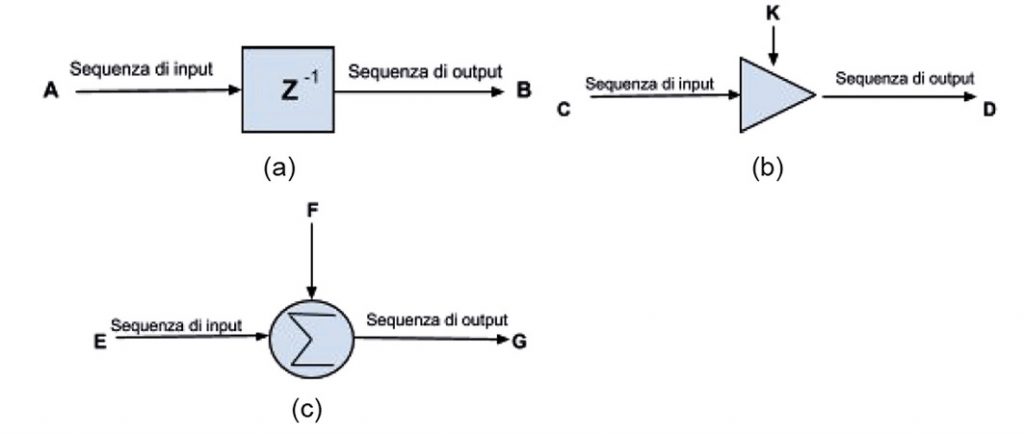
Per implementare un filtro digitale gli elementi base che abbiamo a disposizione sono i seguenti:
1. Memorizzazione per un intervallo di tempo (a): in questo caso l’uscita B è uguale all’ingresso A esattamente T secondi dopo, dove T è il periodo di campionamento
2. Moltiplicazione per una costante (b): D= K*C
3. Somma (c): G= E+F Per comprenderne il funzionamento consideriamo una sequenza di ingresso data da {x(0),x(T),x(2T),…..x(nT)} La sua trasformata Z può essere scritta come:
X(z)=x(0)+x(T)z-1+x(2T)z-2+…x(nT)z-n
Applicando questa sequenza all’ingresso del blocco di memorizzazione indicato nella figura (a) avremo una sequenza di uscita che sarà data da {0,x(0),x(T),x(2T),…..x(nT)} e la sua trasformata Z pari a Y(z)=0+x(0)z-1+x(T)z-2+x(2T)z-3+… x(nT-T)z-n
Dividendo l’uscita per l’ingresso otteniamo Y(z)=H(z)X(z) dove H(z)=z-1 è la funzione di trasferimento del filtro. Procedendo allo stesso modo per il moltiplicatore, avremo che in questo caso non c’è elemento di ritardo quindi l’uscita, se K è la costante moltiplicativa del filtro, risulterà pari a Y(z)=K•X(z). Come esempio consideriamo una sequenza di ingresso {2,5,3,7} e la costante K=5. In uscita avremo la sequenza {10,25,15,35} dove ogni punto della sequenza di uscita occorre nello stesso intervallo di tempo del corrispondente valore dell’ingresso. L’ultimo elemento, il sommatore, considera come ingresso del filtro due sequenze di valori che sono sommate per ottenere la sequenza di uscita. Come nel caso precedente, si assume il caso ideale quindi nessun ritardo temporale per la generazione dell’uscita che quindi risulterà nella sua forma Z-trasformata Y(z)=X1(z)+X2(z) dove X1(z) e X2(z) sono le due sequenze di ingresso. Questa breve introduzione sugli elementi base di un filtro digitale ci permetterà di approfondirne le tipologie e soprattutto le applicazioni. Passo dopo passo, il segnale biologico campionato verrà “ripulito” dalle sue naturali complessità diventando sempre più chiaro per la struttura che andrà a controllare.







