
Il presente articolo introduce brevemente una particolare classe di sistemi a tempo discreto e mostra come a partire dalla caratterizzazione matematica di questi sia possibile estrarre architetture hardware/software ottimizzate per la propria piattaforma.
Un segnale a tempo discreto è rappresentabile matematicamente come una successione numerica. Un sistema a tempo discreto si può quindi definire come un operatore T nello spazio di tali successioni; il sistema si dice lineare e tempo-invariante se verifica le due seguenti proprietà:
(1) linearità
T(αx1[n]+ βx2[n])= αT(x1[n])+ βT(x2[n])
(2) tempo invarianza
∀n0, y[n]=T(x[n]), x1[n]=x[n-n0] ⇒
y1[n]=T[x1[n])=y[n-n0]
Si può dimostrare che per un sistema di questo tipo la risposta ad un qualunque segnale in ingresso può essere rappresentata come prodotto di convoluzione del segnale stesso e della risposta all’impulso, ovvero y[n]=h[n]®x[n] (3)
Uno strumento fondamentale nello studio dei sistemi a tempo discreto è la trasformata z, definita come segue:
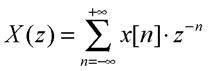
la quale gode di un’interessante proprietà: al prodotto di convoluzione di due segnali corrisponde il prodotto delle relative trasformate. La trasformata z della risposta all’impulso di un sistema viene chiamata funzione di trasferimento H(z); in base alla proprietà sopra citata, la trasformata z della risposta di un sistema ad un generico ingresso si può scrivere come prodotto della trasformata dell’ingresso e della funzione di trasferimento, ovvero y[n]=h[n]®x[n] ⇔ Y(z)=H(z)X(z).
Un sistema è quindi completamente specificato quando siano noti la sua funzione di trasferimento ed il dominio di definizione di questa. Un sistema rappresentabile come serie di due sotto-sistemi è descritto da una funzione di trasferimento che è il prodotto delle funzioni di trasferimento dei componenti; nel caso di architetture parallele invece la funzione di trasferimento si scrive come somma delle componenti. Una classe importante di sistemi lineari e tempo-invarianti sono quelli rappresentati da equazioni lineari alle differenze del tipo seguente:
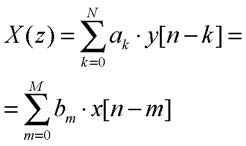
In tal caso, specificate le condizioni iniziali, il sistema può essere ricostruito mediante calcoli ricorsivi. Tale aspetto è di notevole interesse soprattutto nell’ambito dei filtri IIR caratterizzati da una risposta all’impulso con un numero infinito di coefficienti diversi da zero e per i quali, quindi, il calcolo del segnale trasformato mediante applicazione diretta del prodotto di convoluzione (3) risulterebbe irrealizzabile nella pratica. Nel caso di sistemi lineari e tempo invarianti, le condizioni iniziali sono in linea del tutto generale le seguenti:
x[n]=0 ∀ n < n0 ⇒ y[n0-1]=...= y[n0-N]=0 (7).
Per sistemi descritti da una equazione alle differenze, la funzione di trasferimento, come si può facilmente derivare applicando la trasformata z ad entrambi i membri della (6), assume una espressione polinomiale del tipo:
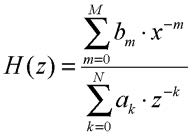
A partire da tale rappresentazione si possono facilmente individuare delle architetture per la realizzazione del sistema che si basano su strutture aritmetiche elementari (come addizionatori e moltiplicatori per una costante) ed elementi di memoria (come linee di ritardo); diverse soluzioni possono essere individuate in funzione delle caratteristiche della particolare applicazione. La trattazione che segue e le architetture traggono spunto da quando discusso in [1], testo di riferimento per la teoria dei sistemi a tempo discreto. La figura 1 mostra, unitamente al loro significato, i simboli che saranno utilizzati nel seguito per la rappresentazione grafica di queste architetture; la figura 1a si riferisce ad una rappresentazione mediante diagramma a blocchi, la figura 1b ad un diagramma di flusso dei dati.
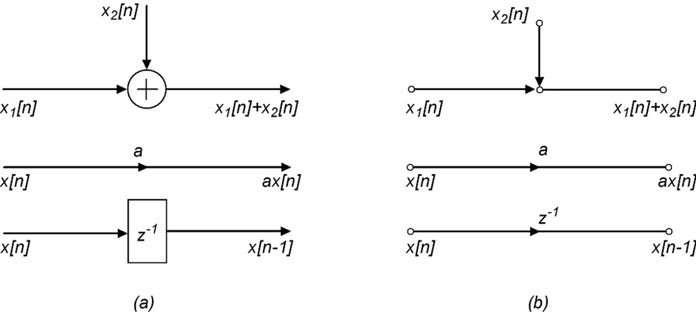
Figura 1: simboli per la descrizione di un sistema a tempo discreto.
Forme dirette
Senza perdere di generalità si può assumere che il coefficiente a0 nell’equazione alle differenze che descrive un sistema lineare tempo invariante sia uguale ad 1; in caso contrario sarà sufficiente dividere per a0 tutti gli altri. La (6) può quindi essere riscritta nel modo seguente:
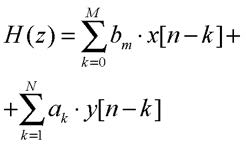
dove, come anticipato in precedenza, appare evidente la possibilità di calcolare l’uscita in maniera ricorsiva. Nella (9) si evidenziano due contributi rappresentabili come somme pesate degli M precedenti campioni in ingresso e degli N precedenti valori calcolati dell’uscita; i pesi di tali somme sono i coefficienti dell’equazione alle differenze. Utilizzando quindi il simbolismo mostrato nella figura 1, si può facilmente derivare la rappresentazione del sistema mostrata in figura 2.
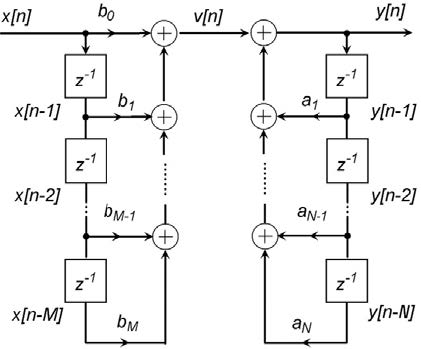
Figura 2: forma diretta di tipo I.
Tale rappresentazione si chiama forma diretta di tipo I. Dalla stessa figura 2, d’altra parte, si evidenzia come il sistema potrebbe in altro modo essere visto come risultante dall’applicazione in sequenza di due sottosistemi, il che equivale, in altri termini, a rappresentare la funzione di trasferimento come segue:
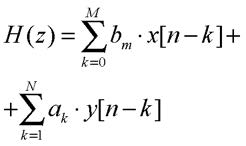
Invertire i due termini della moltiplicazione (il che è lecito vista la proprietà commutativa di questa) equivale ad invertire nella figura 2 la sequenza nella quale i due sottosistemi sono applicati. Il risultato è lo schema di figura 3a; è interessante osservare che in tale rappresentazione si nota immediatamente che alcuni degli elementi di memoria istanziati sono in realtà ridondanti e possono essere rimossi. L’architettura risultante che minimizza il numero di registri è mostrata in figura 3b; tale rappresentazione si chiama forma canonica o forma diretta di tipo II. Le forme dirette di tipo I e II sono teoricamente equivalenti tra loro. Tuttavia nella realizzazione pratica, a causa della rappresentazione in precisione finita dei coefficienti dell’espansione (10) e dei risultati delle somme e moltiplicazioni ai diversi passi, si introducono degli errori che possono modificare anche profondamente il valore dell’uscita rispetto al risultato atteso.
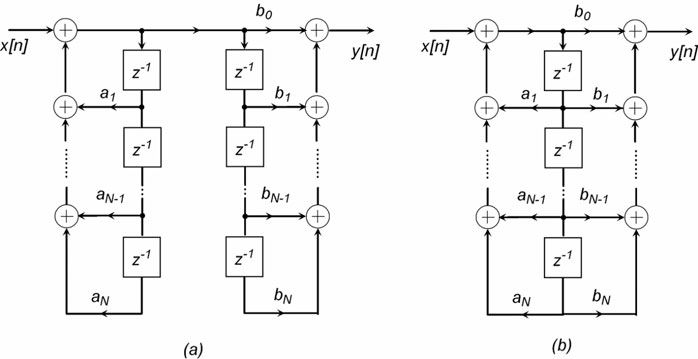
Figura 3: forma diretta di tipo II.
Forme in cascata, parallele e trasposte
Le forme dirette esposte in precedenza sono state ottenute a partire da una rappresentazione polinomiale esplicita della funzione di trasferimento senza nessun accorgimento particolare. In realtà, rappresentando diversamente tale funzione, possono essere evidenziate altre soluzioni architetturali. Consideriamo ad esempio la rappresentazione seguente:
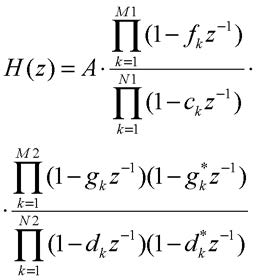
dove numeratore e denominatore sono stati decomposti in polinomi del primo ordine; la presenza di poli e zeri complessi coniugati deriva dall’ipotesi che i coefficienti dell’equazione alle differenze che descrive il sistema siano reali. E’ banale osservare come, in linea teorica, ed in base alle proprietà di composizione dei sistemi enunciate nell’introduzione, il sistema potrebbe essere realizzato come serie di passi elementari ognuno descritto da uno dei termini al primo ordine presente nella (11). Tuttavia questo comporterebbe un utilizzo eccessivo di risorse combinatorie e registrate rispetto a quanto realmente necessario. Nella pratica si preferisce pertanto una soluzione di compromesso in cui i diversi fattori sono raggruppati a due a due in una rappresentazione diversa della (11) del tipo:
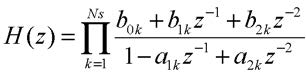
La decomposizione ottenuta si basa su sotto-sistemi del secondo ordine per i quali le forme dirette di tipo I o II possono essere applicate, come mostrato in figura 4 nel caso particolare di un sistema del sesto ordine.
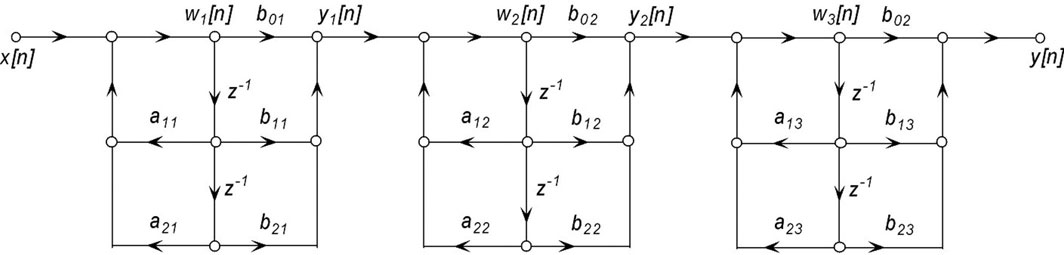
Figura 4: forma seriale.
Disporre di una rappresentazione serie del sistema può essere utile nei casi in cui si intenda ridurre la quantità di risorse occupate. In questo caso, infatti, si può immaginare una soluzione basata su un singolo modulo in grado di calcolare un generico termine del secondo ordine. Il valore dell’uscita può così essere calcolato in Ns cicli di clock; ad ogni ciclo il modulo viene configurato in accordo al passo della (12) che deve eseguire modificando i coefficienti moltiplicativi ed utilizzando come valori d’ingresso i risultati del ciclo precedente. Chiaramente si ha una latenza maggiore nella generazione dell’uscita ed una riduzione del data-rate sostenuto. Una soluzioni parallela si può invece ottenere riscrivendo la funzione di trasferimento (11) come somma di funzioni razionali elementari ottenute mediante divisione polinomiale tra numeratore e denominatore, del tipo:
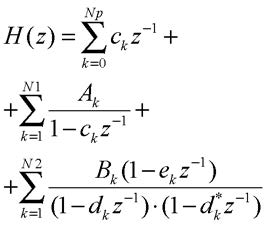
Un’architettura corrispondente di esempio è mostrato in figura 5.
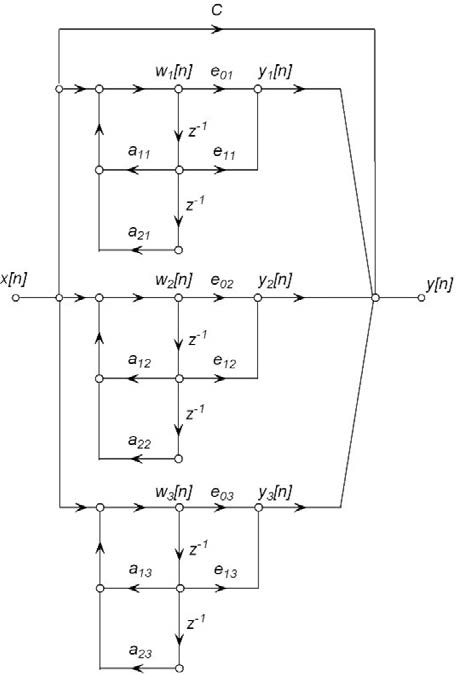
Figura 5: forma parallela.
Più in generale forme alter native della funzione di trasferimento (e quindi realizzazione diverse del sistema) possono ricavarsi applicando la teoria dei grafi alla descrizione di una particolare architettura di riferimento. Una delle proprietà più interessanti dei grafi, ad esempio, è quella di trasposizione la quale stabilisce che in un sistema con singolo ingresso/singola uscita, la funzione di trasferimento non cambia se i nodi di ingresso ed uscita sono scambiati tra loro e la direzione di tutte le connessioni della rete sono invertite. La figura 6b mostra un semplice esempio di applicazione di tale proprietà al caso di un sistema del secondo ordine inizialmente rappresentato (figura 6a) in forma canonica.
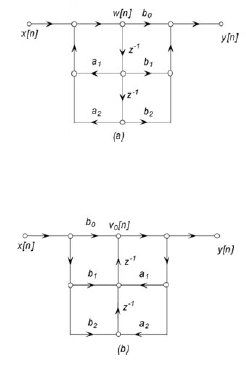
Figura 6: forma trasposta.
Conclusioni
I sistemi a tempo discreto lineari e tempoinvarianti sono ormai diffusamente utilizzati in tutti i campi di applicazione. La teoria di tali sistemi è ben definita; il sistema è univocamente specificato quando siano noti l’equazione alla differenze che soddisfa e le condizioni iniziali, ovvero la funzione di trasferimento ed il relativo dominio di definizione. A partire da questi, è possibile individuare diverse architetture di tipo diretto, in cascata, parallele o trasposte per la realizzazione del sistema. Considerazioni relative alle risorse disponibili nell’architettura selezionata ed alla risoluzione utilizzata nella rappresentazione in aritmetica finita sono i parametri di scelta della soluzione più adeguata alla propria applicazione.




