Ci serviremo di SPICE (nella versione LTspice) per esplorare il comportamento di questi componenti e visualizzarne la risposta in frequenza.
LTspice, il programma di simulazione generosamente reso disponibile da Linear Technology, è sempre più diffuso ed usato, non ha restrizioni nel numero di nodi del circuito e di componenti e grazie anche al supporto di una community online. Una volta installato il programma, operazione semplice e senza alcun problema, installiamo anche la libreria di ferriti Laird (ex Steward), reperibile in Rif 2. L’installazione in LTspice funziona perfettamente come descritto nel file di documentazione contenuto nello zip della libreria. Notare che la procedura suggerita non funziona, invece, con le ultime release di Pspice.
L’autore ha scelto per la sua applicazione di filtraggio di una alimentazione sensibile al rumore, il componente LI603D301-R10. Si tratta di una ferrite bead con impedenza tipica di 300 ohm a 100 MHz, corrente massima 400 mA, componente a montaggio superficiale in contenitore 0603. Simuliamo il componente da solo per cominciare (vedere schema in figura 1), con relativo risultato in figura 2.
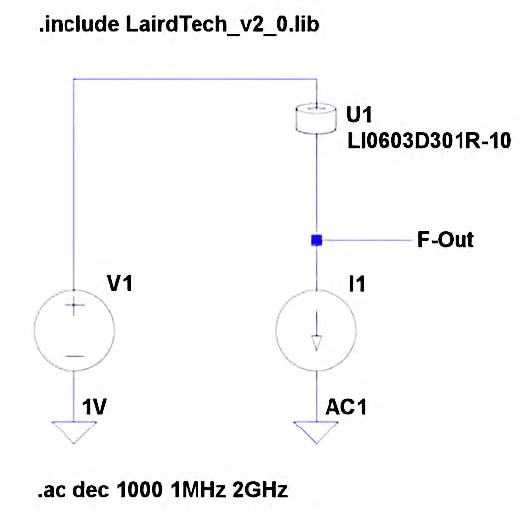
Figura 1: schema Simulazione Ferrite isolata.
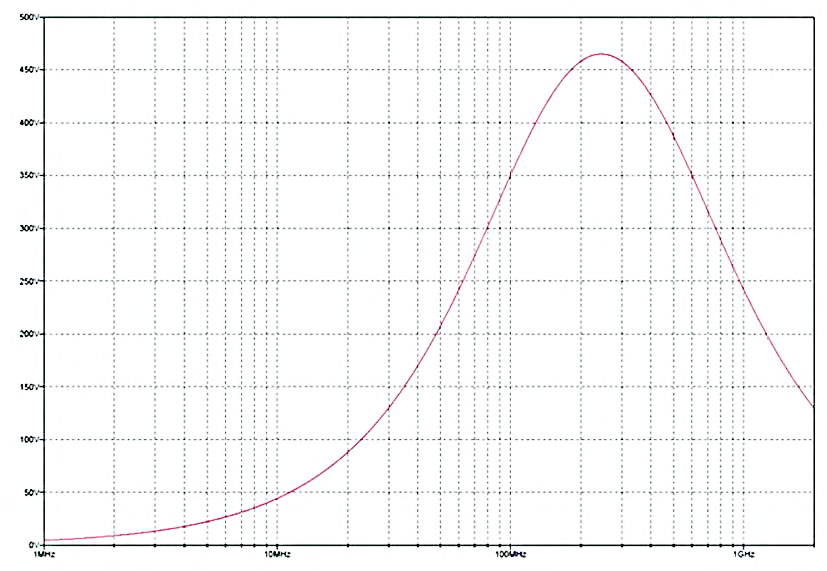
Figura 2: simulazione Ferrite isolata.
Applicando tensione e corrente unitaria e variando la frequenza simulazione AC), otteniamo la curva che rappresenta l’impedenza in funzione della frequenza per il componente scelto. Avendo un generatore da 1A, la tensione coincide numericamente con l’impedenza in ohm e possiamo, quindi, leggere l’impedenza ad ogni frequenza in ohm sulle ordinate del grafico. Ritroviamo l’andamento descritto nell’articolo precedente, come atteso. A bassa e media frequenza l’impedenza è relativamente bassa, la ferrite ha basse perdite ferromagnetiche e si comporta, quindi, come un induttore. A frequenze maggiori di qualche MHz, i fenomeni dissipativi prevalgono e l’impedenza aumenta fino a presentare un picco per poi decrescere. L’efficacia della ferrite diminuisce perché inizia ad essere cortocircuitata dalla capacità parassita, come visto. Per il componente scelto, il picco si ha nei dintorni di 250 MHz ma l’impedenza si mantiene significativa fino a ben oltre 1 GHz, promettendo una certa efficacia nel filtraggio del rumore ad alta frequenza. Notiamo che sia il valore di impedenza ad una data frequenza, sia la frequenza a cui abbiamo il picco di massima impedenza, sono un po’ diversi da quanto indicato dal datasheet. Questo approssimazione può essere in parte dovuta alla corrente di carico in continua (abbiamo usato 1A per un componente con corrente nominale di 0.4A), ma si consiglia comunque di acquisire misure sul componente scelto per applicazioni critiche ed, eventualmente, procedere ad un aggiustamento fine dei parametri del modello Spice. Purtroppo tali misure richiedono strumentazione costosa e non sempre facilmente reperibile, quali Impedance Analyzer o Network Analyzer. Qualcosa si può fare ricorrendo ai vecchi ma affidabili ponti di misura in alternata, almeno per frequenze non troppo elevate. I metodi di misura a ponte sono riportati in qualunque testo di misure elettriche. Chi volesse approfondire caratteristiche, funzionamento ed applicazioni dei Network Analyzer, potrebbe trovare utile la documentazione Agilent in Rif 3. I più coraggiosi ed amanti del do-ityourself, sono invitati a dare un’occhiata a Rif 4, a proprio rischio e pericolo, ovviamente. Proviamo ora a completare progressivamente il circuito in cui la ferrite è inserita e verificarne il comportamento a livello sistema invece che singolo componente. Aggiungiamo, quindi, un condensatore da 100 nF che rappresenta il decoupling locale dell’alimentazione che intendiamo filtrare (figura 3 e 4).
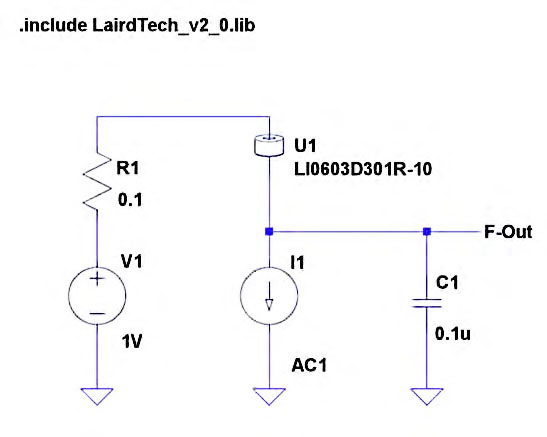
Figura 3: schema simulazione Ferrite e condensatore di decoupling (100nF).
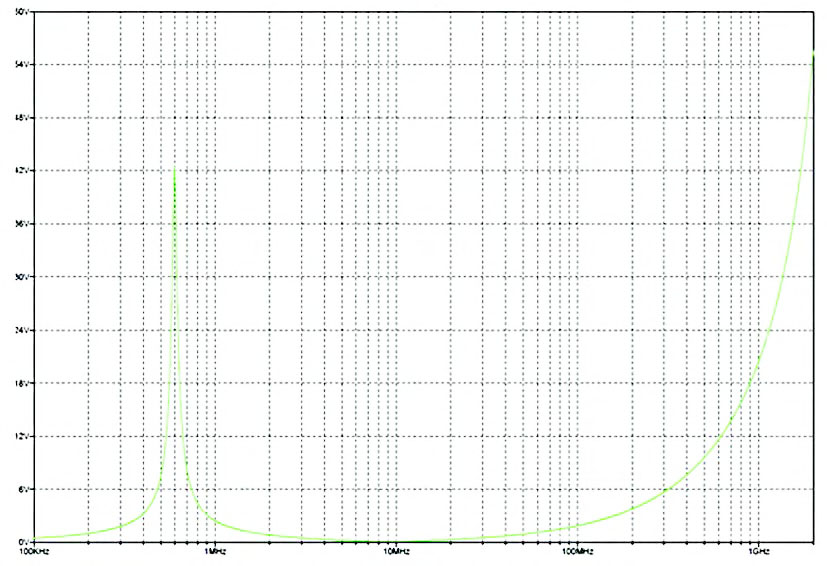
Figura 4: simulazione Ferrite e condensatore di decoupling (100nF).
Per rendere le cose un po’ più realistiche, useremo un generatore non più ideale, quindi con una certa resistenza interna, rappresentata da R1. Estraiamo la curva di impedenza, con simulazione Spice AC, come fatto in precedenza. Notiamo che viene introdotto un picco di antirisonanza, di impedenza elevata, a bassa frequenza. Per meglio studiare il fenomeno, aggiungiamo anche il carico previsto, 180 ohm nel nostro caso (figura 5 e 6).
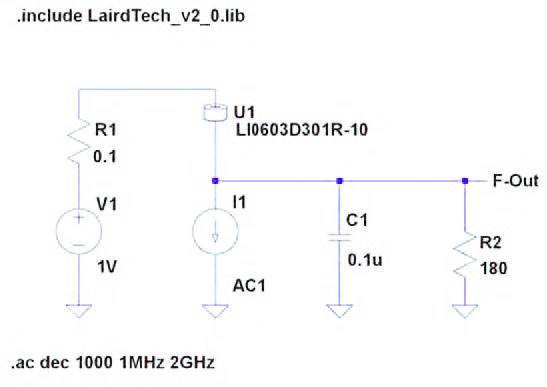
Figura 5: schema Simulazione ferrite, decoupling e carico (180 ohm).
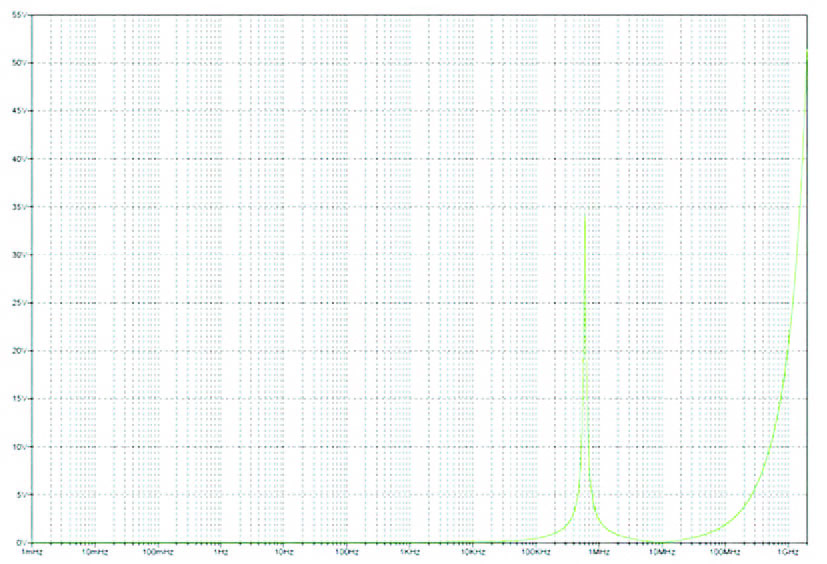
Figura 6: simulazione ferrite, decoupling e carico (180 ohm).
Notiamo che il picco risulta solo leggermente ridotto. Riducendo il carico a 18 ohm (figura 7), abbiamo una apprezzabile riduzione del picco di impedenza, confermando che l’antirisonanza introdotta dall’elemento reattivo ferrite dipende dal valore dell’elemento reattivo di decoupling, insieme all’induttanza della ferrite, ma anche dalle impedenze di sorgente e carico in gioco.
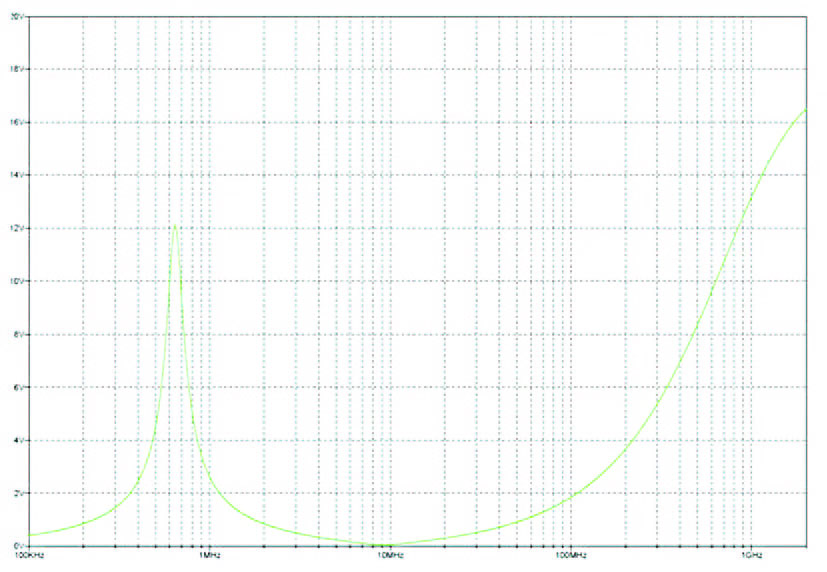
Figura 7: simulazione ferrite, decoupling e carico (18 ohm).
Prima di rilasciare il circuito è quindi indispensabile procedere ad una accurata caratterizzazione in simulazione, tenendo conto delle reali condizioni di lavoro nell’applicazione specifica (e possibilmente ottenere conferma sperimentale sui circuiti critici). Il picco di impedenza può essere accettabile o meno in funzione della banda passante del circuito in oggetto. Se abbiamo una sovrapposizione, è opportuno procedere all’eliminazione del picco, ad esempio, smorzandolo con la tecnica del polo dominante (figura 8).
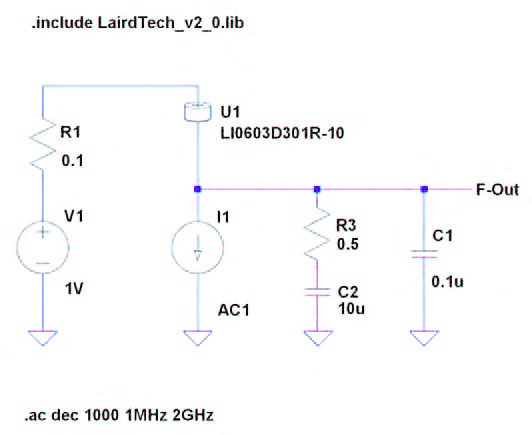
Figura 8: smorzamento di antirisonanze con tecnica del polo dominante.
In pratica, interveniamo sulla caratteristica della rete LC aggiungendo un resistore ed un condensatore. Il dimensionamento del circuito è spiegato in dettaglio nel documento in Rif 5. La cosa fondamentale da verificare è che l’impedenza vista dal carico nella soluzione circuitale finale, sia adeguata nell’intero range di frequenza operativa del carico stesso. A causa della presenza del filtro, tutta la carica necessaria a sostenere domande di corrente istantanee da parte del carico, non potrà provenire dall’alimentatore ma dovrà essere soddisfatta dal decoupling locale, a valle della ferrite. In altre parole, il rispetto dell’impedenza target in frequenza del nostro carico, costituirà il criterio finale di accettazione del filtro implementato. Avremo, quindi, bisogno di disporre di stime affidabili circa il profilo di corrente assorbita dal circuito che intendiamo proteggere, cosa che potrebbe non rivelarsi facile. Abbiamo visto come l’uso delle ferriti sia effettivamente problematico ma utile. Le difficoltà nascono dalla forte non linearità dei componenti, dagli effetti collaterali creati dalle interazioni tra componenti e dalla difficoltà nel procurarci i dati necessari al dimensionamento e verifica dei circuiti.