
Questo articolo descrive nel dettaglio un algoritmo utilizzabile per calcolare i tempi di risposta dei task schedulati in modo prioritario da un sistema operativo real-time assieme alla tecnica di assegnamento di priorità Deadline Monotonic. Conoscere i tempi di risposta permette di stimare con precisione i tempi di risposta di un insieme di task e di verificare se un sistema sia o meno schedulabile.
I sistemi di controllo digitale sono spesso implementati come un insieme di attività periodiche a diverse frequenze attivate da eventi esterni. Questo corrisponde ad avere diverse attività concorrenti gestite tramite l’utilizzo di un task per ogni frequenza di campionamento. Consideriamo adesso la schedulazione di Figura 1, che mostra una schedulazione composta da tre task τ1, τ2 e τ3, con tempi di calcolo C1=2, C2=3, e C3=1 e periodi T1=6, T2=8, e T3=10 unità di tempo.
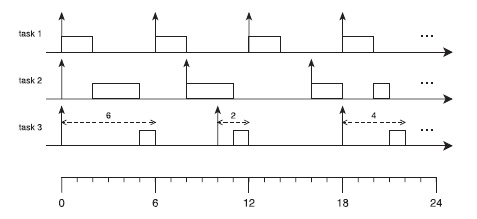
Figura 1. Una schedulazione a priorità fissa composta da tre task con assegnamento di priorità basato su Rate Monotonic
Utilizzando l’assegnamento di priorità Rate Monotonic, il task τ1 avrà la priorità massima, mentre τ3 avrà la priorità minima. Focalizziamo l’attenzione sul task τ3 (di cui le prime tre esecuzioni sono mostrate in Figura 1). Il comportamento del task dipende in modo sostanziale dallo stato del sistema al momento di arrivo della attività. In alcuni casi, infatti, l’esecuzione del task viene “ritardata” in quanto al momento dell’arrivo il sistema sta eseguendo attività a più alta priorità: ad esempio, la prima istanza arriva all’istante 0 e termina all’istante 6, in quanto al momento di arrivo il sistema deve eseguire attività più importanti costituite dai task τ1 e τ2. Definiamo pertanto il tempo di risposta di un task il tempo che intercorre tra la richiesta di una azione, e la sua esecuzione. In Figura 1, sono evidenziati i tempi di risposta delle varie esecuzioni di τ3, che sono di 6, 2 e 4 unità di tempo. Stimare esattamente il tempo di risposta massimo di un task è molto importante. Per prima cosa, un task periodico con un tempo di risposta massimo superiore alla lunghezza del periodo non rispetterà in alcune situazioni i propri vincoli temporali. Inoltre, il tempo di risposta influenza la qualità di implementazione di un algoritmo di controllo: supponendo una implementazione in cui ciascun task effettua in sequenza una acquisizione di un sensore, il relativo calcolo e la corrispondente attuazione, la conoscenza del tempo di risposta massima di un task permette di avere una buona stima del ritardo sull’attuazione rispetto ad una condizione ideale di esecuzione in tempo 0. Lo scopo di questo articolo è quello di presentare una tecnica, denominata response Time Analysis, per il calcolo dei tempi di risposta massima dei task quando essi vengono schedulati utilizzando un sistema a priorità fisse.
LA RESPONSE TIME ANALYSIS
La prima domanda che bisogna porsi nel calcolo del tempo di risposta di un insieme di task è: quando è che i task presentano il massimo tempo di risposta? Se consideriamo i testi del sistema come indipendenti, il tempo di risposta di un task è influenzato dal contributo dei soli task a più alta priorità (i task a più bassa priorità infatti non effettuano mai preemption sul task considerato). Tale contributo viene denominato interferenza. L’interferenza dei task a più alta priorità raggiunge il suo massimo quando tutti i task a più alta priorità vengono attivati assieme al task considerato, in un istante che viene denominato istante critico. L’esempio mostrato in Figura 1 mostra i task del sistema che partono tutti assieme all’istante 0, provocando la massima interferenza sul task τ3. Il calcolo della interferenza è stato studiato per la prima volta da Audsley[1], ed è descritto di seguito. In generale, possiamo considerare un sistema composto da un insieme di task T={τi}, dove ciascun task τi ha una priorità, un tempo massimo di esecuzione Ci (denominato spesso WCET - Worst Case Execution Time), ed un periodo Ti. Il tempo di risposta Ri di un task τi, pertanto, potrà essere calcolato utilizzando la semplice formula:
Ri=Ci+Ii
dove Ii rappresenta l’interferenza massima subita da una istanza di un generico task τi. Tale interferenza è in generale costituita dalla somma dei tempi di esecuzione dei task a più alta priorità che fanno preemption interrompendo il task corrente. In altre parole, più è grande il tempo di risposta di un task, più il fattore di interferenza di quel task aumenta, in quanto ci sono più istanze dei task ad alta priorità che interrompono il task considerato. Da queste parole, è facile capire come il fattore di interferenza Ii dipenda dal tempo di risposta Ri di un task. Supponendo che i task siano ordinati per priorità decrescente (τi ha priorità maggiore di τi+1), l’interferenza Ii di un task τi è costituita dalla somma dei contributi di tutti i task a priorità più alta (l’indice k della sommatoria copre tutti i task con indice fino ad i-1). I contributi all’interferenza sono costituiti dal numero di istanze del task τk (ciascuna di lunghezza massima Ck) che possono interferire in un periodo di tempo dato dal tempo risposta del task τi. Pertanto, la formula completa utilizzabile per il calcolo del tempo di risposta di un task è:
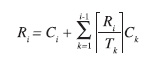
La risoluzione di tale equazione non è banale, in quanto l’incognita Ri è presente all’interno dell’estremo superiore all’interno della sommatoria. Uno dei metodi utilizzabili per ricavare Ri è quello di utilizzare una formula iterativa, che converge al tempo di risposta di un task quando l’utilizzazione del processore è minore di 1. In particolare, la soluzione iterativa ha la seguente espressione:
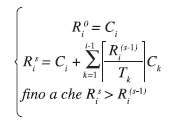
Ovvero, al primo passo il tempo di risposta include solo il tempo di calcolo del task sotto analisi. A partire dal secondo passo, vengono aggiunti i contributi di interferenza. Occorre iterare il calcolo fino a che il tempo di risposta non converga ad un valore definito. A quel punto, il tempo di risposta trovato è il massimo tempo di risposta del task considerato. Il tempo di risposta del task può essere confrontato successivamente con la propria deadline relativa per comprendere se il task sia o meno schedulabile.
UN ESEMPIO
In questo esempio, andremo a calcolare il tempo di risposta del task τ3 in Figura 1. Come accennato precedentemente, il tempo di risposta della esecuzione delle istanze di τ3 varia a seconda delle preemption dei task a più alta priorità. Il risultato dell’algoritmo corrisponderà pertanto al massimo tempo di risposta possibile per l’esecuzione di qualsiasi istanza del task. Al primo passo il tempo di risposta è posto uguale al tempo di calcolo del task, ovvero:
R30=C2=l
Al secondo passo, occorre aggiungere la interferenza causata dai task τ1 e τ2, calcolata utilizzando il valore del tempo di risposta al passo precedente. Il calcolo da effettuare è il seguente:
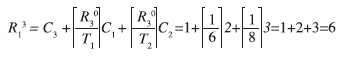
Effettuare un altro passo dell’algoritmo. Al terzo passo, occorre applicare di nuovo la stesa formula del passo precedente, con il valore del tempo di risposta aggiornato. Il calcolo da effettuare è il seguente:
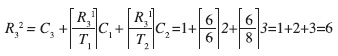
Come si può notare, l’algoritmo ha raggiunto la convergenza, in quanto R30=R31. Il valore trovato corrisponde all’istante critico, ovvero quello in cui tutti i task ad alta priorità partono assieme. Tale situazione è mostrata nella Figura 1, in cui il task τ3 ha, appunto, un tempo di risposta di 6 unità di tempo. Notare infine come un incremento del tempo di calcolo del task τ3 di una unità comporti un aumento del tempo di risposta di ulteriori 6 unità (il task τ3 in questo caso non rispetterebbe il proprio vincolo di periodicità). In altre parole, la relazione esistente tra tempo di calcolo di un task ed il suo tempo di risposta non è lineare ma è una funzione “a gradini”.
DEADLINE MONOTONIC
Ci sono alcuni casi nell’implementazione di sistemi di controllo digitale, in cui si ha il desiderio di garantire che l’esecuzione di alcune attività avvenga il più vicino possibile al loro istante di attivazione. A livello di modello, tale situazione può essere indicata specificando una deadline minore del periodo del task. Questo permette di avere un comportamento più vicino al caso ideale, in cui i task eseguono utilizzando un tempo 0, e permette di limitare il jitter esistente tra il momento dell’attivazione e l’esecuzione del task. Un esempio tipico può essere il calcolo della scintilla in un sistema di controllo motore, per cui l’attività che calcola l’istante della scintilla deve essere eseguita molto vicino all’arrivo dell’interrupt dell’encoder collegato alla rotazione dell’albero motore. In questi casi, può essere utilizzato un assegnamento di priorità alternativo a quello Rate Monotonic. Tale assegnamento di priorità è denominato Deadline Monotonic [1], e prevede per ogni task la specifica, oltre ad un tempo di calcolo massimo e ad un periodo, di una deadline relativa minore o uguale al periodo del task. L’assegnamento di priorità Deadline Monotonic prevede la specifica di una priorità inversamente proporzionale alla deadline relativa. In altre parole, i task con deadline più breve (più urgente) ricevono una priorità più alta indipendentemente dal loro periodo di esecuzione. In generale, avere una deadline minore del periodo comporta implicitamente che l’utilizzazione del tempo di calcolo non è uniforme del tempo, e per questa ragione non esistono formule chiuse come nel caso di Rate Monotonic che permettano di capire se un sistema implementato con un assegnamento di priorità Deadline Monotonic sia schedulabile. Per effettuare tale verifica è comunque sufficiente calcolare il tempo di risposta di ciascun task usando la tecnica della Response Time Analysis mostrata in questo articolo, verificando che i tempi di risposta di ciascun task siano inferiori alle corrispondenti deadline relative.
RIFERIMENTI
[1] N. C. Audsley, A. Burns, M. Richardson, and A. Wellings: “Hard Real-Time Scheduling: The Deadline Monotonic Approach”, IEEE Workshop on Real-Time Operating Systems, 1992




