
La metodologia data-driven ha attirato molta attenzione recentemente nella comunità fisica. Questo non è sorprendente poiché uno degli obiettivi fondamentali della fisica è quello di dedurre o scoprire le leggi della fisica dai dati osservativi. Il rapido sviluppo della tecnologia dell'Intelligenza Artificiale fa sorgere la domanda se queste scoperte possano essere eseguite algoritmicamente dai computer. In questo articolo parleremo del fisico Hong Qin, programmatore di un algoritmo di apprendimento che, da un insieme di dati osservativi su un reticolo spaziale, usa la teoria di campo appresa da una AI per prevedere nuove osservazioni. L'approccio di apprendimento delle teorie di campo discrete supera le difficoltà associate all'apprendimento delle teorie continue da parte dell'Intelligenza Artificiale e predice correttamente altre orbite planetarie del Sistema Solare, senza necessità di imparare o conoscere le leggi del moto di Newton e la gravitazione universale. Gli algoritmi proposti dovrebbero essere applicabili anche agli effetti della Relatività Speciale e della Relatività Generale.
Un approccio nuovo
L'apprendimento automatico non è un concetto nuovo in fisica. In particolare, la connessione tra reti neurali artificiali e sistemi dinamici è nota da decenni.
Qual è il nuovo contributo portato dallo studio del professor Hong Qin del Princeton University Program in Fisica del Plasma?
La maggior parte delle attuali applicazioni delle tecniche di apprendimento automatico in fisica rientrano nelle seguenti categorie:
- Usare le reti neurali per modellare processi fisici complessi, come le interruzioni del plasma nei dispositivi di fusione magnetica e lo stress effettivo di Reynolds dovuto alla turbolenza
- Risolvere equazioni differenziali in fisica matematica approssimando le soluzioni con reti neurali
- Scoprire funzioni sconosciute o parametri indeterminati in equazioni differenziali
- Utilizzo di reti neurali per generare dati di campionamento in insiemi statistici per il calcolo delle proprietà di equilibrio di sistemi fisici
Il problema affrontato in questo articolo appartiene a una nuova categoria. Il metodo proposto "impara" una teoria di campo da un dato insieme di dati di addestramento che consistono in valori di un campo fisico osservati in alcune posizioni spaziali. Le leggi della fisica sono fondamentalmente espresse sotto forma di teorie di campo, invece di equazioni differenziali. Poiché le teorie di campo sono in generale più semplici delle corrispondenti equazioni differenziali, l'apprendimento delle teorie di campo è più facile, il che è vero sia per l'intelligenza umana che per quella artificiale. A parte l'assunzione fondamentale che i dati osservativi sono governati dalle teorie di campo, gli algoritmi di apprendimento e di servizio proposti non presuppongono alcuna conoscenza delle leggi della fisica, come la legge del moto di Newton e l'equazione di Schrödinger. Questo è diverso dalla maggior parte delle metodologie esistenti di apprendimento automatico in fisica.
Gli algoritmi di autoapprendimento delle teorie di campo discrete
L'apprendimento di una teoria di campo discreta direttamente dai dati di addestramento e il suo successivo utilizzo costituiscono un approccio interessante per la scoperta di modelli fisici da parte dell'Intelligenza Artificiale. L'algoritmo di apprendimento delle teorie di campo discrete appartiene alla famiglia degli algoritmi geometrici che conservano la struttura, ed hanno dimostrato di essere superiori agli algoritmi convenzionali basati sulla discretizzazione delle equazioni differenziali. L'efficacia del metodo e degli algoritmi sviluppati è dimostrata utilizzando gli esempi di oscillazioni non lineari ed il problema di Keplero, cioè il problema del moto di un corpo in un campo di forze centrali. Nel caso specifico gravitazionale, abbiamo in particolare che la forza centrale è direttamente proporzionale all’inverso del quadrato della distanza. Per una teoria di campo discreta, il campo è definito su un reticolo spaziale etichettato da due indici interi (i, j). Per semplicità, adottiamo un reticolo rettangolare mostrato in Figura 1.
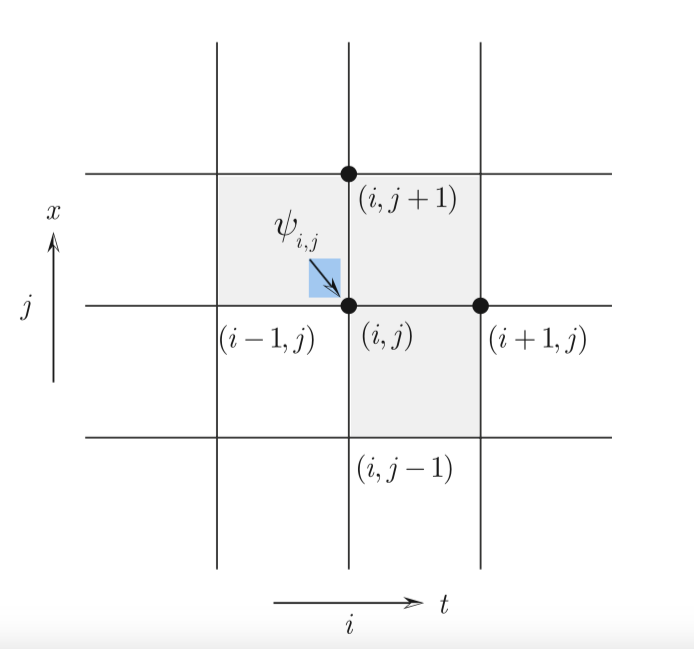
Figura 1: Il reticolo spaziale come campo discreto
Il primo indice i identifica i punti della griglia temporale, e il secondo indice j i punti della griglia spaziale. L'azione discreta del sistema è la sommatoria delle densità su tutte le celle della griglia. A differenza della difficile situazione per l'apprendimento di una teoria di campo continua, l'apprendimento di una teoria di campo discreta è semplice. Basta impostare un'approssimazione dell'azione utilizzando una rete neurale o qualsiasi altro schema di approssimazione adeguato. Si possono applicare algoritmi differenziali automatici, che sono stati ampiamente adottati nelle reti neurali artificiali. Per addestrare la rete neurale o altra approssimazione, sono disponibili metodi consolidati, tra cui l'algoritmo di ricerca delle radici di Newton e l'ottimizzatore di Adam. Una volta che la densità è addestrata, la teoria di campo discreta appresa è pronta per essere utilizzata per prevedere nuove osservazioni. Dopo aver specificato le condizioni al contorno, l'equazione data per descrivere il problema viene risolta per il campo discreto.
L'Apprendimento Automatico applicato al problema di Keplero
Come abbiamo visto, il problema di Keplero rappresenta il moto di un corpo in un campo a forze centrali. In questo caso particolare, l'algoritmo di apprendimento impara la teoria di campo da un insieme di dati di orbite planetarie simili a quelle che Keplero ereditò da Tycho Brahe nel 1601; si tratta quindi di misurazioni della parallasse planetaria, fenomeno per cui un oggetto sembra spostarsi rispetto allo sfondo se si cambia il punto di osservazione, accurate al minuto d'arco. Perché questo test nell'utilizzo dell'algoritmo? Keplero impiegò 5 anni per scoprire la sua prima e seconda legge del moto planetario, e altri 78 anni prima che Newton risolvesse il problema kepleriano usando le sue leggi del moto e della gravitazione universale. Appare evidente quindi come prevedere l'osservazione possa aiutare a velocizzare la soluzione del problema.
Per semplicità, i dati sono le orbite di Mercurio, Venere, Terra, Marte, Cerere e Giove, generate risolvendo l'equazione del moto di Newton, per un pianeta nel campo gravitazionale del Sole, secondo la legge di gravitazione universale di Newton. Le lunghezze della scala di normalizzazione spaziale e temporale sono rispettivamente 1 a.u. e 58,14 giorni, e i passi temporali dei dati orbitali sono 0,05 giorni. Ricordiamo che l'obiettivo non è quello di riscoprire le leggi di Keplero del moto planetario o le leggi di Newton del moto e della gravitazione universale attraverso l'apprendimento automatico. Si tratta invece di allenare una AI ad una teoria di campo discreta dalle orbite visualizzate in Figura 2 per poi prevedere nuove orbite planetarie.
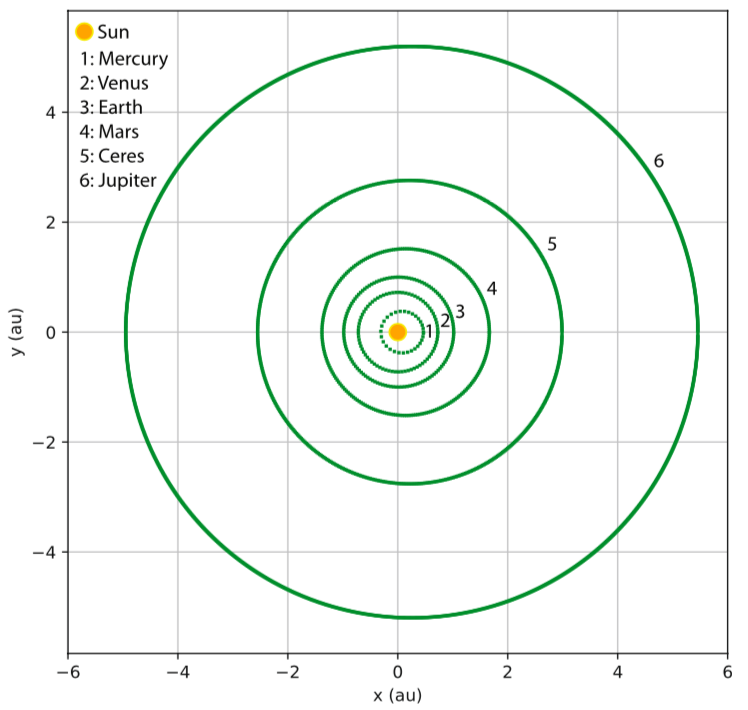
Figura 2: Le orbite di Mercurio, Venere, Terra, Marte, Cerere e Giove generate risolvendo l'equazione del moto di Newton per un pianeta nel campo gravitazionale del Sole secondo la legge di gravitazione universale di Newton. Queste orbite sono i dati di allenamento per la teoria di campo discreta
Per modellare il problema si utilizza una rete neurale completamente connessa con due strati nascosti, ognuno dei quali ha 40 neuroni con la funzione di attivazione. La rete è inizializzata in modo casuale con una distribuzione normale, e poi addestrata dall'ottimizzatore Adam fino a quando la perdita media su un singolo punto della griglia temporale è ridotta di un fattore 105 rispetto al suo valore iniziale. Partendo dalle stesse condizioni iniziali delle orbite di addestramento, l'algoritmo addestrato predice le orbite tracciate con i marcatori rossi in Figura 3, rispetto alle orbite di addestramento indicate dai marcatori verdi.
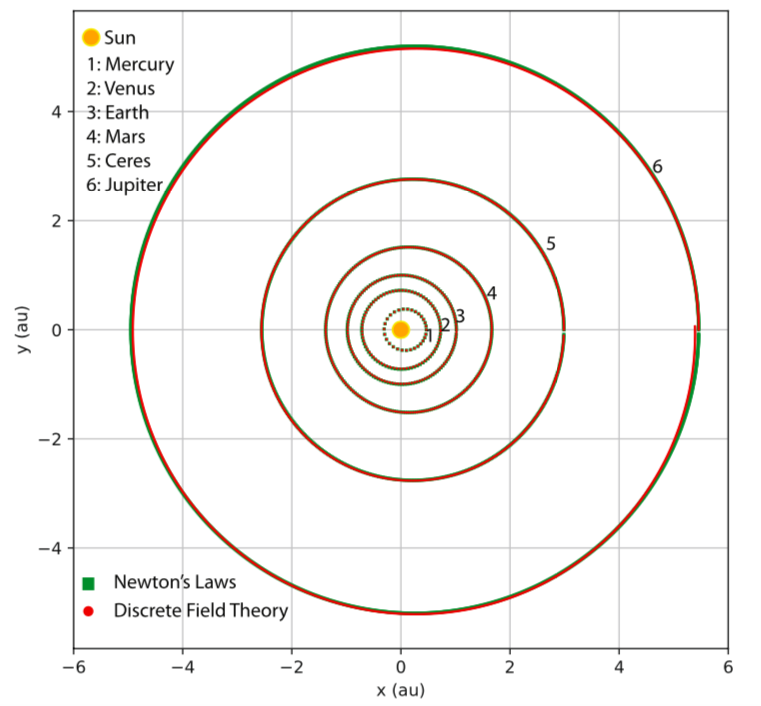
Figura 3: Orbite di Mercurio, Venere, Terra, Marte, Cerere e Giove. Le orbite indicate dai marcatori rossi sono generate dalla teoria del campo discreto appresa. Le orbite indicate dai marcatori verdi sono le orbite di allenamento della Figura 2
È degno di nota che la teoria del campo discreto addestrata predice correttamente le orbite di fuga paraboliche e iperboliche, anche se le orbite di addestramento sono tutte ellittiche, come si vede nelle Figure 2 e 3. Storicamente, Keplero sosteneva che le orbite di fuga e le orbite ellittiche sono governate da leggi diverse. Fu Newton che scoprì la dipendenza da 1/r del campo gravitazionale dalle leggi del moto planetario di Keplero e unificò le orbite ellittiche e quelle di fuga sotto la stessa legge fisica. I risultati mostrati nelle Figure 4 e 5 mostrano che gli algoritmi di apprendimento automatico e di servizio risolvono il problema di Keplero in termini di previsione corretta delle orbite planetarie senza conoscere o imparare le leggi del moto di Newton e la gravitazione universale.
ATTENZIONE: quello che hai appena letto è solo un estratto, l'Articolo Tecnico completo è composto da ben 2037 parole ed è riservato agli ABBONATI. Con l'Abbonamento avrai anche accesso a tutti gli altri Articoli Tecnici che potrai leggere in formato PDF per un anno. ABBONATI ORA, è semplice e sicuro.







Grazie Maila per questo splendido articolo. Mi chiedevo, essendo quindi secondo la teoria della gravità quantistica lo spaziotempo fatto di grani, se siano in corso ricerche per applicazioni AI al fine di ottenere indizi per validare tale teoria. In tal senso credo che il passo successivo dell AI sarebbe quello che finora abbiamo solo visto nei film di fantascienza, il viaggio nel tempo!
Grazie Giuseppe!
Facendo qualche ricerca non mi risulta per ora che ci siano esperimenti in questo senso; ma la meccanica quantistica non è il mio settore specifico, quindi potrebbe essermi sfuggito qualcosa. In ogni caso mi pare presto per parlare di viaggio nel tempo! Anche se la teoria fosse verificata non tutti sono d’accordo sul fatto che si possa realizzare. Inoltre bisognerà fare attenzione alle possibili implicazioni. Credo che dovremo aspettare ancora un po’!