
Gli operatori orientati ai bit sono sicuramente uno degli aspetti più rilevanti nei sistemi embedded; infatti, in questo modo è possibile accedere, direttamente, ai singoli bit dei dispositivi hardware. É universalmente riconosciuto, poi, che questi operatori non possono essere applicati a variabili di tipo float o double.
Le informazioni, siano essi concetti astratti o meno, sono rappresentati all’interno di della macchina come una successione di bit, magari formattati secondo un preciso schema. Ad esempio, un tipo char è identificato come un insieme di otto bit, mentre gli altri tipi, ad esempio un intero, utilizzano una numero maggiore di bit. La figura 1 mostra una rappresentazione di alcuni tipi in relazione alla diversa rappresentazione numerica utilizzata, mentre la tabella 1 pone in evidenza l’occupazione di memoria utilizzate, resta, in ogni caso, inteso che queste sono fortemente dipendenti dall’architettura utilizzata.
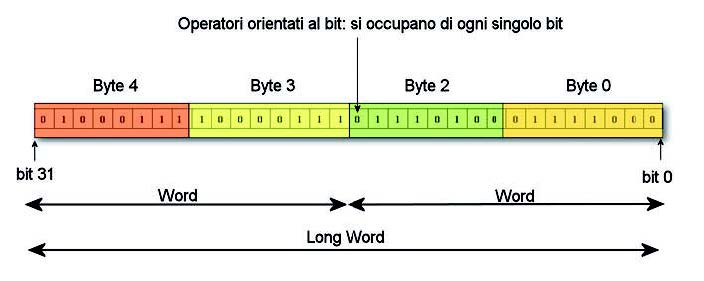
Figura 1: bit, byte, word, e long word.
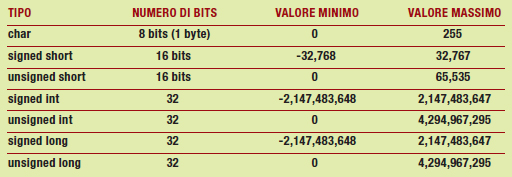
Tabella 1: Occupazione di memoria in relazione ai tipi utilizzati.
Quando abbiamo la necessità, in un sistema embedded, di scrivere programmi, o parti di essi, che devono controllare dispositivi fisici, allora si ha la necessità di disporre operazioni che controllino i singoli bit. Quando ci riferiamo alle operazioni sui singoli bit vogliamo semplicemente attribuire ai bit i due soli valori possibili: zero o uno rispetto ai valori che assume un variabile di tipo char (da 0 a 255). La gestione dei bit, o bitwise, è direttamente relazionabile con il tipo di architettura utilizzata e per le operazioni di questo tipo si utilizzano, di norma, interi senza segno. Il riquadro a pagina seguente mostra uno schema riepilogativo delle operazioni orientati ai bit con le tavole logiche associate. Occorre fare attenzione a non confondere & con && (& e’ “bitwise and”, mentre && e’ “logical and”); la stessa cosa vale per | e ||.
Operazioni sui singoli bit
Le operazioni permesse sui singoli bit non sono molte. L’operatore & (AND) vale 1 se e solo se entrambi i numeri valgono 1. Così, il risultato dell’AND bitwise tra 7 e 2 è pari a 2. Di solito un operatore di questo tipo è, una volta predisposta un‘opportuna maschera, orientato al controllo di determinati bit. Per esempio, il valore MASK contiene alcuni bit a uno, l’esempio seguito deve controllare se il bit 4 ha un valore pari a 1:
MASK b = 50;
if ( b & 0x10 )
cout << “Bit four is set” << endl;
else
cout << “Bit four is clear” << endl;
Per quanto riguarda l’OR e lo XOR bitwise, essi seguono le stesse identiche regole dell’AND bitwise, salvo che la tavola di verità è diversa (nel caso dell’OR, viene restituito 1 se almeno uno dei numeri vale 1, nel caso dello XOR viene restituito 1 se i numeri sono diversi, e 0 se sono uguali; infatti, XOR significa “exclusive or, “or esclusivo”: rispetto all’OR, restituisce 0 anche se i due numeri valgono entrambi 1). Esiste poi l’operatore complemento: questo effettua il complemento ad uno, ovvero l’operazione di inversione di tutti i bit. In pratica, ogni bit a valore 0 viene cambiato ad 1, e viceversa. Proviamo a capire il funzionamento con la seguente porzione di codice
BYTE b = ~0x03;
cout << “b = “ << b << endl;
WORD w = ~0x03;
cout << “w = “ << w << endl;
Questa produce il seguente risultato:
00000011 - 0x03
11111100 - ~0x03 b
0000000000000011 - 0x03
1111111111111100 - ~ 0x03 w
Il complemento a uno è un operatore unario, cioè opera su un solo argomento indicato a destra dell’operatore. Gli operatori >> e << si preoccupano di spostare a destra o a sinistra il valore di un numero di tante volte quante sono le posizioni espressamente specificate; si inseriscono, poi, altrettanti, pari a zero, valori in base a quante sono le posizioni specificate nelle posizioni altrimenti lasciate vuote. Così, se volessimo spostare a destra il valore 4, 00000100 in binario, di due posizioni otterremmo il valore 00000001. Allo stesso modo, uno spostamento a sinistra sempre del valore 4 di tre posizioni otterremmo il valore 00100000. Da questo è possibile dedurre che uno spostamento a destra di un bit vuol dire dividere il valore per due, mentre uno spostamento a sinistra equivale a moltiplicarlo. Gli operatori di shift (spostamento o scorrimento) eseguono un appropriato shift dall’operatore indicato a destra a quello indicato a sinistra. L’operatore destro deve essere positivo. Così:
z<<2 sposta i bit in z di due posti verso sinistra cosi’, se z=00000010 (binario) o 2 (decimale) allora, z>>=2 => z=00000000 (binario) o 0 (decimale) inoltre, z<<=2 => z=00001000 (binario) o 8 (decimale)
L’operazione shift è molto più veloce della reale moltiplicazione (*) o divisione (/); così, se occorrono veloci moltiplicazioni o divisioni per 2 si può utilizzare lo shift. Infatti, con l’esempio
BYTE b = 12;
cout << “b = “ << b << endl;
BYTE c = b << 2;
cout << “c = “ << c << endl;
c = b >> 2;
cout << “c = “ << c << endl;
Si produce il seguente risultato:
00001100 - b
00110000 - b << 2
00000011 - b >> 2
Il listato 1 fornisce un breve esempio, una funzione (bitcount) che somma 2 bit settati ad 1 con un numero ad 8 bit (unsigned char) passato come argomento alla funzione.
int bitcount(unsigned char x)
{int count;
for (count=0; x!=0; x>>=1);
if (x&01)
count++;
return count;
}
| Listato 1 - bitcount |
Dall’esempio vediamo che il loop “for” non viene usato per semplici operazioni di somma x>>=1 => x=x>>1. Il loop “for” sposta, ciclicamente, a destra x, finche’ x diventa 0. Il controllo “if” utilizza la valutazione dell’espressione x &01, si controlla il primo bit di x, ed esegue count++ se questo è 1.
Bit field
I bit field, o campi di bit, rispondono all’esigenza di ottimizzare l’occupazione di memoria. Infatti, con i bit field si compattano diversi oggetti in una parola di memoria utilizzando un intero attraverso un insieme di bit adiacenti. L’esempio che mostriamo pone in evidenza la struttura in C di una data rappresentata con campi di bit, o bit field.
struct date_struct {
BYTE day : 5, // 1 to 31
month : 4, // 1 to 12
year : 14; // 0 to 9999
} date;
Il valore numerico accanto a ciascun campo identifica la quantità di bit allocati; in questo modo l’occupazione totale di date_struct è di 23 bit, cioè tre byte dove l’ultimo bit non è utilizzato. Disporre di una struttura di questo tipo permette di accedere ai singoli campi direttamente secondo questa locuzione:
date.day = 12;
Di solito un compilatore utilizza la rappresentazione minima di un byte per allocare una struttura di questo tipo. Tuttavia, se si richiede una quantità superiore a un byte (ad esempio, 9 bit), allora il compilatore utilizza un altro byte. La figura 2 mostra un altro esempio, un registro di controllo per un driver di un disco e il listato 4 è la struttura associata secondo la notazione bit field.
Libreria Bit Operations
Il listato 2 mostra una libreria per la gestione dei bit.
#ifndef BITOPS__H
#define BITOPS__H
#include <stdio.H>
#include <stdlib.h> /* For size_t */
#include <limits.h> /* For CHAR_BIT */
#include “sniptype.h” /* For TOBOOL() */
#include “extkword.h” /* For CDECL */
/*** Macros to manipulate bits in any integral data
type. */
#define BitSet(arg,posn) ((arg) | (1L << (posn)))
#define BitClr(arg,posn) ((arg) & ~(1L << (posn)))
#define BitFlp(arg,posn) ((arg) ^ (1L << (posn)))
#define BitTst(arg,posn) TOBOOL((arg) & (1L << (posn)))
/*** Macros to manipulate bits in an array of char.
* These macros assume CHAR_BIT is one of either 8, 16,
or 32. */
#define MASK CHAR_BIT-1
#define SHIFT ((CHAR_BIT==8)?3:(CHAR_BIT==16)?4:8)
#define BitOff(a,x) ((void)((a)[(x)>>SHIFT] &= ~(1
<< ((x)&MASK))))
#define BitOn(a,x) ((void)((a)[(x)>>SHIFT] |= (1 <<
((x)&MASK))))
#define BitFlip(a,x) ((void)((a)[(x)>>SHIFT] ^= (1
<< ((x)&MASK))))
#define IsBit(a,x) ((a)[(x)>>SHIFT] & (1 <<
((x)&MASK)))
/*** BITARRAY.C */
char *alloc_bit_array(size_t bits);
int getbit(char *set, int number);
void setbit(char *set, int number, int value);
void flipbit(char *set, int number);
/*** BITFILES.C */
typedef struct {
FILE * file; /* for stream I/O */
char rbuf; /* read bit buffer */
char rcnt; /* read bit count */
char wbuf; /* write bit buffer */
char wcnt; /* write bit count */
} bfile;
bfile * bfopen(char *name, char *mode);
int bfread(bfile *bf);
void bfwrite(int bit, bfile *bf);
void bfclose(bfile *bf);
/*** BITSTRNG.C */
void bitstring(char *str, long byze, int biz, int
strwid);
/*** BSTR_I.C */
unsigned int bstr_i(char *cptr);
/*** BITCNT_1.C */
int CDECL bit_count(long x);
/*** BITCNT_2.C */
int CDECL bitcount(long i);
/*** BITCNT_3.C */
int CDECL ntbl_bitcount(long int x);
int CDECL BW_btbl_bitcount(long int x);
int CDECL AR_btbl_bitcount(long int x);
/*** BITCNT_4.C */
int CDECL ntbl_bitcnt(long x);
int CDECL btbl_bitcnt(long x);
#endif /* BITOPS__H */
| Listato 2 - bitops.h |
Le quattro macro mostrano le possibili operazioni permesse sui bit, come set o clear. Le macro hanno due parametri in ingresso: arg e posn. Con <arg> si identifica la variabile su cui i dovrà applicare l’oerazione logica, mentre con posn si specifica la posizione del bit coinvolto.
Così con posn==0, l’espressione che dovrà essere valutata è:
0000 0000 0000 0000 0000 0000
0000 0001 notazione binaria
mentre con posn==8
0000 0000 0000 0000 0000 0001
0000 0000 notazione binaria
In altre parole, semplicemente crea un campo di zeri con un uno alla posizione specificata. Solo la macro BitClr() è leggermente differente. Il listato 3 mostra un esempio d’uso di questa libreria, si pongono anche in evidenza, il codice macchina prodotto di una architettura Intel, l’occupazione e l’efficienza del codice.
#define BOOL(x) (!(!(x)))
#define BitSet(arg,posn) ((arg) | (1L << (posn)))
#define BitClr(arg,posn) ((arg) & ~(1L << (posn)))
#define BitTst(arg,posn) BOOL((arg) & (1L << (posn)))
#define BitFlp(arg,posn) ((arg) ^ (1L << (posn)))
int bitmanip(int word)
{
word = BitSet(word, 2);
word = BitSet(word, 7);
word = BitClr(word, 3);
word = BitFlp(word, 9);
return word;
}
—— Risultato : codice generato ———————————————————————-
Module: C:\BINK\tst.c
Group: ‘DGROUP’ CONST,CONST2,_DATA,_BSS
Segment: _TEXT BYTE 00000008 bytes
0000 0c 84 bitmanip_ or al,84H
0002 80 f4 02 xor ah,02H
0005 24 f7 and al,0f7H
0007 c3 ret
No disassembly errors
| Listato 3 - Test di una piccola applicazione |
struct DISK_REGISTER {
unsigned ready:1;
unsigned error_occured:1;
unsigned disk_spinning:1;
unsigned write_protect:1;
unsigned head_loaded:1;
unsigned error_code:8;
unsigned track:9;
unsigned sector:5;
unsigned command:5;
};
| Listato 3 - Rappresentaione del disk controller |
Precedenze tra operatori
In ogni linguaggio di programmazione esistono delle regole. Per esempio, occorre rispettare un preciso ordine di precedenza che coinvolge anche gli operatori bitwise così come in ogni espressione matematica. Infatti, secondo le regole della matematica, l’espressione 2x + 7 * 21 equivale a 2x + 147, perché la moltiplicazione ha precedenza maggiore della somma. Per sovvertire l’ordine di precedenza, basta usare le parentesi. Nell’esempio di prima, scrivendo (2x + 7) * 21, se x valesse 1, l’espressione varrebbe (2*1 + 7) * 21, cioè (2 + 7) * 21 cioè 9 * 21, uguale ad 189. Tuttavia, nei linguaggi di programmazione si ha a che fare con un numero decisamente superiore di operatori, rispetto ai consueti calcoli matematici. La tabella 3 mostra la lista delle precedenze ammissibili nel linguaggio C con le relative priorità.
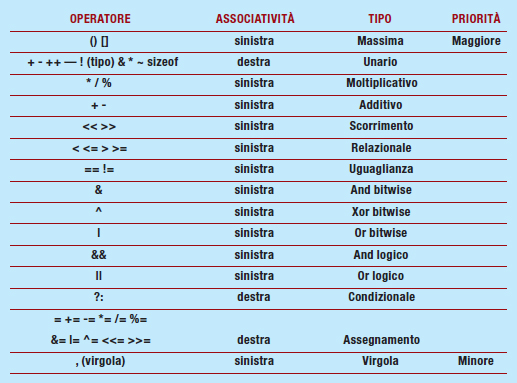
Tabella 3: Associatività e priorità.
Dove non diversamente specificato, gli operatori vengono valutati da sinistra a destra. Con la seguente relazione c = a + b l’operatore + utilizzerebbe come primo operando a, e come secondo b; vale a dire, secondo la notazione algebrica come +(a,b). Invece con c += a l’operatore += utilizzerebbe come primo operatore a, e come secondo c, valutando, appunto, da destra a sinistra. Nel caso, leggermente più complesso, come c += a + b vi sarebbero due operatori: il primo, il + “semplice” (quello più a destra), valuterebbe “normalmente” da sinistra a destra, prendendo come primo operando a, e come secondo b; il secondo, il +=, valuterebbe da destra a sinistra, usando come primo operando il risultato di a+b, e come secondo c.
Conclusioni
Dal sito è possibile scaricare una libreria in C, diffusa secondo la nota formula public domain, per la gestione degli operatori orientati ai bit. La tabella 4 elenca i diversi file inclusi nella distribuzione e descrive il loro uso.
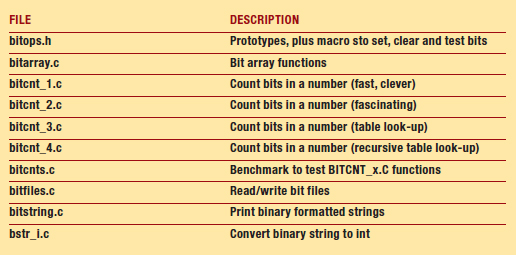
Tabella 4: file




Sto avendo modo, proprio in questi tempi, di creare un piccolo driver. Non ho mai riflettuto sul fatto di usare gli shift per eventuali moltiplicazioni o divisioni per 2. Grazie.
Gli operatori sui bit sono miracolosi. Guarda come si fa lo “swap” tra 2 variabili, senza usare assegnazioni numeriche o variablili temporanee ma solo operatori binari:
x = 123
y = 456
x = x xor y
y = x xor y
x = x xor y
print x —> 456
print y ->>> 123
Interessante. Grazie.