
La distribuzione Raspbian per Raspberry Pi contiene, tra i propri software preinstallati, anche il famoso pacchetto Mathematica. Un formidabile programma per l'esplorazione totale della matematica, in tutti i suoi settori. Vediamone assieme le potenzialità e gli ambiti d'uso, preannunciando che esso costituisce, con ogni probabilità, il programma più usato al mondo, sia nelle università che in ambito professionistico e di ricerca.
Introduzione
La premessa è d'obbligo: sul sito di Raspberry Pi è riportato, nella sezione download, la seguente clausola:
Mathematica and the Wolfram Language are included in this release under license and with permission of Wolfram Research, Inc. and may be used for non-commercial purposes only. By using this software you agree to be bound by the Wolfram Raspberry Pi Bundle Licensee Agreement available here.
Quindi l'accettazione della licenza deve prevedere il solo utilizzo in ambiti non commerciali e privati. Il programma Mathematica è distribuito gratuitamente sul sistema operativo. Si tratta di un potente programma di calcolo e programmazione nel campo della scienza, matematica, ingegneria e tante altre discipline. Praticamente fa tutto!
La sua esplorazione richiederebbe letteralmente milioni di pagine di documentazione. Qui ci limiteremo solo ad esaminare alcune possibilità operative. La sua esecuzione avvia il notebook di Mathematica, ossia una specie di editor nel quale è possibile scrivere un comando o un intero programma. Esso inizialmente è vuoto, come mostra la figura 1.
Figura 1: Il Notebook di Mathematica.
Il funzionamento del tasto "Invio" è un po' diverso dal solito. Premuto da solo, non conferma il comando immesso ma il cursore si posizione semplicemente a capo, in attesa di un nuovo statement o un nuovo comando. Per confermare, invece, l'operazione digitata, occorre premere insieme i tasti "Shift" + "Invio". In questo caso Mathematica processerà la digitazione dell'utente e visualizzerà il risultato, come mostrato in figura 2.
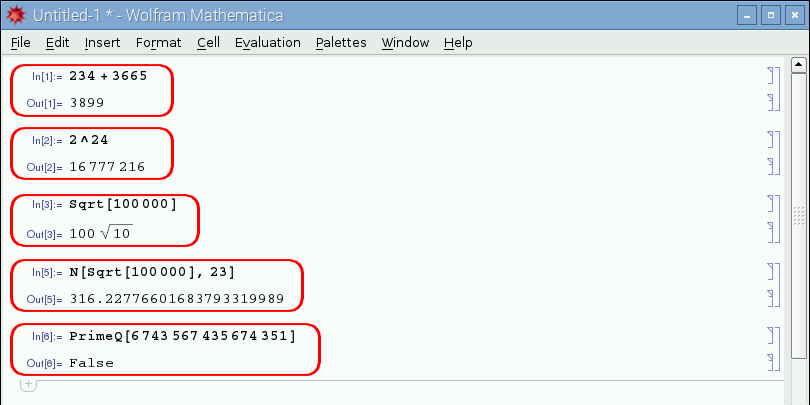
Figura 2: Alcuni calcoli nel notebook.
Liste
Mathematica è molto potente nel gestire le liste. Si tratta di una collezione di dati, racchiusa tra parentesi graffe. Una lista può contenere tutto: oggetti, numeri, disegni, variabili, valori o altre liste. Esiste un set di comandi dedicati alle liste, per processare e gestire in toto questi potenti contenitori di dati.
Precisione infinita
Una delle particolarità di Mathematica è quella di gestire la precisione arbitraria, ovvero una potenza di calcolo non dipendente dall'architettura della macchina. In questo modo è possibile eseguire operazioni matematiche composte da migliaia (o anche milioni) di cifre, con risultati sorprendenti. La figura 3 mostra alcuni esempi di calcoli enormi, con alcune elevazioni a potenza.
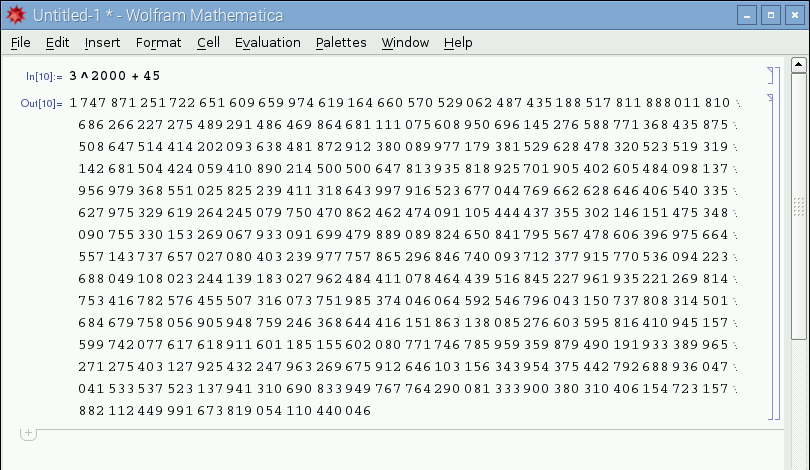
Figura 3: La precisione infinita di Mathematica.
Grafici
Anche la creazione di un grafico è una operazione molto semplice. Si può utilizzare la funzione Plot per ottenere un grafico dell'espressione desiderata specificando, altresì, l'intervallo del suo dominio. La figura 4 mostra il classico andamento del Coseno.
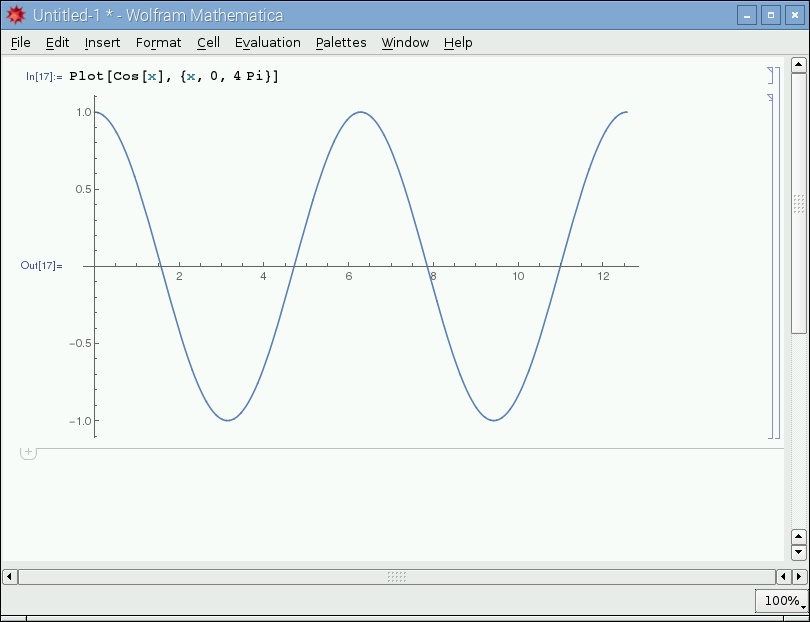
Figura 4: Il grafico della funzione coseno(x).
Iterazioni
Una singola operazione può essere ripetuta a piacimento utilizzando gli iteratori, come in qualsiasi linguaggio di programmazione che si rispetti. In figura 5 è possibile osservare un esempio di looping.
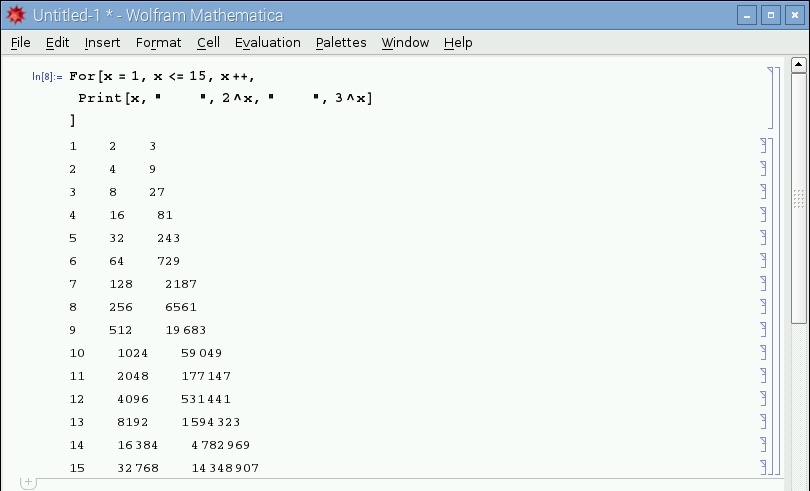
Figura 5: operazioni in Loop.
Calcoli simbolici ed espansioni
Mathematica è un potente calcolatore simbolico. Con esso è possibile effettuare operazioni con simboli, riduzioni, semplificazioni ed espansioni. La figura 6 mostra l'espansione di un binomio di 5° grado.
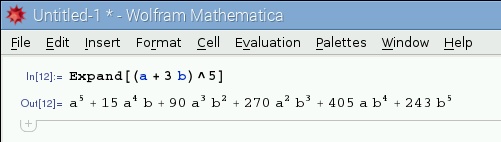
Figura 6: L'espansione di un binomio di 5° grado.
Help
L'aiuto in linea è uno dei punti di forza di matematica. Ogni funzione, come si vede in figura 7, può essere consultata nell'ambito dello stesso programma, scrivendo il comando:
? NomeFunzione
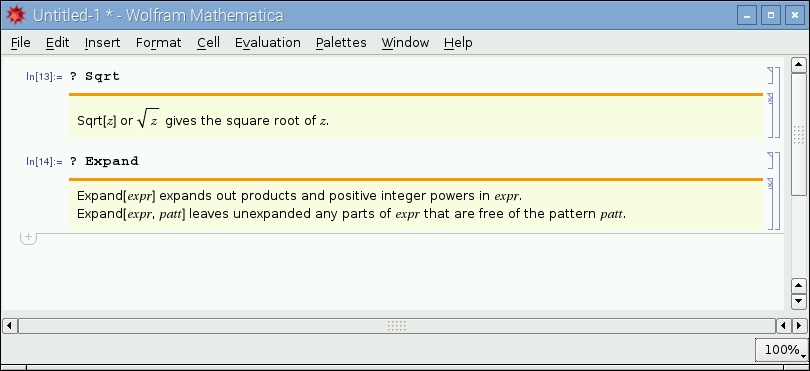
Figura 7: L'aiuto di sintassi on-line.
Conclusioni
Il breve spazio a disposizione non consente di dare la dovuta e meritata importanza a questo gioiello della programmazione. Ci auguriamo che in un prossimo futuro, anche a richiesta dei lettori, possa essere iniziato un corso di base su Mathematica.




Il Raspberry Pi: uno strumento di “conversione” commerciale: grazie ad esso molte aziende e produttori di software a pagamento stanno distribuendo alcuni famosi programmi, gratuitamente. Mathematica e Windows 10 IoT sono alcuni dei più blasonati prodotti che l’utente può utilizzare in tutta tranquillità e con la coscienza a posto…
Per gli amanti della matematica, e non solo, un software decisamente da provare e avere sul proprio Raspberry Pi.
Secondo me la potenza di Mathematica deriva dal fatto che ogni istruzione è una “funzione”, ma non nel senso dell’analisi matematica, per cui può inglobare qualunque oggetto, anche grafico. Un esempio è dato dalle cosiddette “macchine ricorsive”. Ci sono quelle per così dire, numeriche, che agiscono su numeri. Con Mathematica, invece, è possibile lavorare su “macchine ricorsive topologiche”, come nel caso dell’insieme di cantor:
http://tinyurl.com/m5yhcd9
Riguardo la gestione delle “liste” (vettori, matrici, tensori, e non solo), non ci sono dubbi: Mathematica è insuperabile. Leggevo su un forum che Maxima (l’alternativa open source a Mathematica) non è allo stesso livello di Mathematica.
Forse il vero rivale di Mathematica, è Maple, un CAS molto utilizzato dai fisici che lavorano nell’ambito della Relatività Generale, poiché Maple ha un package sul calcolo tensoriale. Anche Mathematica dispone di un simile package, ma è a pagamento, in quanto sviluppato da altri. Tra l’altro, il calcolo tensoriale dipende fortemente dall’ambito considerato, quindi il package sul calcolo tensoriale di Mathematica, è molto più complicato di quello di Maple.
In ambito elettronico/elettrotecnico c’è il package NODAL.
Una curiosità: esiste una versione free (online) di Mathematica: Mathics http://mathics.github.io/
Bel link
Uso molto anche wolframalpha.com
Gran bei motori computazionali.
Il bello di Mathematica è che abbraccia proprio tutti i lati della matematica.
forse l’unica nota dolente è il prezzo 🙁 (compreso quello dei package che si comprano a parte)
Per quanto riguarda la gestione delle liste (che sembra essere il punto forte di Mathematica), chiediamo: Maxima, Maple, altri, sono in grado di risolvere certi problemi?
È da qualche settimana che sto dietro questo problema: simulare la discontinuità della distribuzione dei numeri primi attraverso la distribuzione degli zeri della funzione zeta di Riemanna. Sia chiaro, non sto dicendo nulla di nuovo perchè si tratta di un vecchio articolo di due matematici svedesi che negli anni 70 eseguirono dei calcoli a partire dalla formula di Riemann-von Mangold. Sto cercando di scrivere, appunto, un programma con Mathematica. Il problema è il numero di “chiamate” (circa 700000) della parte reale della funzione esponenziale integrale che non è elementarmente esprimibile, per cui ogni volta Mathematica deve calcolare un integrale complesso (!). Però, operando sulle LISTE anziché sui NUMERI, il carico computazionale dimunuisce di molto. A questo punto penso sia una proprietà generale, nel senso che certe funzioni non elementarmente esprimibili, si comportano alla stregua di “generatori di discontinuità” per funzioni continue. Per ora sono allo step zero, nel senso che ho elaborato una routine valida in generale: http://tinyurl.com/mdm9hft
I Numeri Primi…. grande argomento che amo.
Sono (ero) ricercatore (p190) di Primi nel sito del Prof. Caldwell al sito
primes.utm.edu
Nel 2006 scoprii un big numero primo, composto da ben 479944 cifre.
Il mio numero e’ 58753*2^1594323-1 e al momento della sua scoperta occupata il 39° posto della classifica mondiale dei numeri primi… Un vero gioiello per quei tempo.
Adesso e’ sceso di classifica per ora verso il 2000° posto, per via di nuove scoperte.
Ho lasciato perdere perche’ le bollette della luce erano troppo care, avevo un super six core AMD, 3600 Mhz…….
Bei tempi…..
http://primes.utm.edu/primes/lists/all.txt
Sapevo questo, l’avevo letto sul tuo profilo…
Al contrario, io non ne so molto di numeri primi, però è ormai da un bel pò che mi “sbatto” con Mathematica e funzioni “complicate”.
A questo punto, vorrei tentare di modificare la parte reale degli zeri della zeta di Riemann (che secondo la famigerata congettura è 1/2) per vedere quello che succede nella distribuzione dei primi…
Proprio l’altra settimana ho scoperto una proprieta’ dei numeri primi (veramente degli pseudoprimi o PRP). Ma e’ computazionalmente onerosa da computare, stilo piccolo test di Fermat, ma e’ eccezionalmente semplice….. L’ho provato per molti piccoli primi e funziona…
La distribuzione dei numeri pseudoprimi venne utilizzata da John Nash nel tentativo di dimostrare la Congettura di Riemann. Sarebbe interessante leggere gli scritti di Nash dell’epoca. Ma temo siano introvabili. Sul libro “Storia di John Nash, matematico e folle” (da cui venne tratto il famoso film “A beautiful mind”) ci sono un paio di capitoli dedicati a questa vicenda.
Riguardo al paper dei matematici svedesi, alla fine ho scritto una routine con Mathematica, e c’è voluto un bel pò di tempo per elaborare questo grafico http://www.extrabyte.info/00lips77.gif che riproduce i primi otto numeri primi utilizzando la congettura di Riemann.
Fantasico. Complimenti!!!
Sono ancora in alto mare 🙁 . Sia chiaro, non è mia intenzione dimostrare Riemann, visto che matematici con gli attributi non ci sono riusciti…
Cmq a differenza dei matematici svedesi che hanno svolto un’analisi “globale”, nel senso che hanno ricostruito i primi nell’intervallo reale [0,100], vorrei svolgere un’analisi “locale”. Ad esempio, considero il contributo proveniente da almeno una cinquantina di zeri (ma forse anche più) in un intorno del numero primo 3, considerando poi una parte reale diversa da 1/2 (cioè negando la congettura di Riemann).
ps. Segnalo quest’articolo http://www.scientiajournal.org/review/index.php/Scientia/article/view/37/80 di Diego Marin che, purtroppo, non è stato preso in considerazione da nessuno…