
Le deep neural network possono assumere diverse forme, ognuna delle quali adatta all'esecuzione di un particolare task. Nel precedente articolo, abbiamo già approfondito i concetti alla base delle Convolutional Neural Network (CNN), reti utilizzate per compiti come il riconoscimento degli oggetti o l'elaborazione del linguaggio naturale. E' però sempre utile avere un 'feedback pratico' della teoria, e toccare con mano, per quanto possibile, i risultati che è possibile ottenere sfruttando questi strumenti, magari adoperando delle librerie già pronte e (relativamente) semplici da utilizzare. In quest'ottica, in questo articolo parleremo di MatConvNet, uno strumento che si è imposto come standard de facto per l'implementazione delle CNN in ambiente MATLAB, tanto da essere consigliato nella documentazione ufficiale, e vedremo come è possibile addestrare una rete, anche complessa, o utilizzare modelli già pronti, adattandoli alle nostre esigenze.
Introduzione
Fino a qualche anno fa, implementare una deep neural network era un semplice esercizio accademico: non esistevano strumenti ottimizzati, i tempi necessari all'addestramento erano praticamente infiniti, ed i risultati lasciavano alquanto a desiderare. Oggi, però, chiunque abbia un minimo di conoscenza informatica, assieme ad un computer dotato di una GPU abbastanza recente, può cimentarsi nell'impresa, sfruttando uno dei tanti framework preposti allo scopo. In particolare, in questo articolo parleremo di MatConvNet, toolbox per MATLAB sviluppato da Andrea Vedaldi, dell'Università di Oxford, che offre numerose funzioni per semplificare lo sviluppo di una CNN, permettendoci di concentrarci sul modello, piuttosto che sull'implementazione dei singoli layer, ed offrendo un buon compromesso tra flessibilità, facilità di utilizzo, e performance.
Prima di proseguire, però, avremo bisogno di una conoscenza almeno basilare di MATLAB: se non lo avete ancora fatto, leggete il relativo tutorial base, e poi, per approfondire, quello un po' più avanzato. Inoltre, avere un po' di conoscenza delle immagini digitali può aiutare, ed anche per questo abbiamo un tutorial.
Hello, MatConvNet!
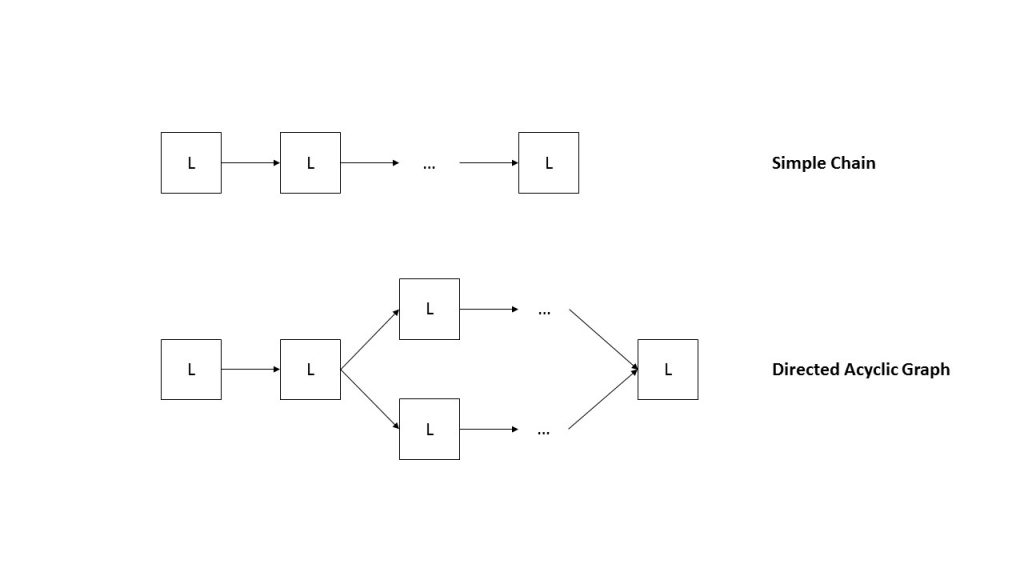
Iniziamo con il sottolineare un'importante analogia: infatti, le reti neurali e i grafi sono, dal punto di vista concettuale, analoghi. Se immaginiamo, infatti, che i nodi di un grafo rappresentino i singoli neuroni della rete, allora i lati descriveranno il flusso dei dati. MatConvNet, a partire da questa intuizione, definisce due strutture fondamentali, riassunte in figura 1: da un lato, abbiamo le simple chain network, date dalla successione 'semplice' dei singoli strati, mentre dall'altro i directed acyclic graphs (DAGs), strutture più complesse in cui è possibile osservare diverse ramificazioni.
Graph.Supponiamo ora di voler utilizzare le CNN per un task di object recognition: essenzialmente, potremo usare due approcci. Da un lato, potremmo definire un nuovo modello di rete, addestrarlo su uno dei dataset disponibili (o, nel caso avessimo esigenze specifiche, crearne uno da zero), e, una volta terminato l'addestramento, utilizzarlo; dall'altro, invece, potremmo utilizzare un modello già definito e funzionante, che ben si adatti ai nostri scopi. Con MatConvNet sono possibili entrambi gli approcci, e li introdurremo nel prosieguo dell'articolo.
Passi preliminari
Una premessa: potete trovare il codice utilizzato in quest'articolo in un'apposita repository GitHub. Cloniamola usando git:
git clone https://github.com/anhelus/eos_matlab_matconvnet.git
L'unico requisito per utilizzare il codice è, ovviamente, l'aver installato MATLAB, in una versione abbastanza recente, sul proprio computer; il consiglio è comunque quello di provare ad implementare il codice nella restante parte dell'articolo, usando la repo come reference.
Creiamo, adesso, un nuovo script MATLAB, ed adottiamo una 'good practice' che andrebbe sempre seguita, inizializzando i parametri necessari all'esecuzione del nostro programma, e definendo le librerie che utilizzeremo, eventualmente aggiungendole al path mediante la funzione addpath. Inoltre, usiamo la funzione unzip per effettuare il download di MatConvNet, ed estrarla in una cartella che chiamiamo libsFolder:
unzip('https://github.com/vlfeat/matconvnet/archive/master.zip', libsFolder);
A questo punto, è necessario seguire la procedura di configurazione di MatConvNet, che segue due passi: nel primo, è necessario compilare parte delle funzioni che compongono la libreria, usando la funzione vl_compilenn; ovviamente, assicuriamoci di avere installato un compilatore C (gcc su Linux, MinGW o anche il compilatore di Visual Studio su Windows) e di aver configurato MATLAB usando l'istruzione mex -setup. Notiamo, inoltre, che se abbiamo a disposizione una GPU CUDA-enabled, è possibile specificare l'opzione di compilazione enableGpu, che ci mette a disposizione la potenza offerta dal GPGPU. Scriviamo quindi le seguenti istruzioni:
if (gpuDeviceCount > 0)
g = gpuDevice;
if str2double(g.ComputeCapability) > 3
compileGpu = true;
end
end
vl_compilenn('enableGpu', compileGpu);
Nelle istruzioni precedenti, valutiamo innanzitutto la presenza di GPU CUDA-enabled; in caso positivo, se la potenza computazionale della nostra scheda grafica è sufficiente (il parametro 3 è arbitrario), impostiamo l'opzione di compilazione enableGpu a true. Completiamo la configurazione di MatConvNet utilizzando la seguente funzione di configurazione:
vl_setupnn;
Prepariamo i dati
Una volta configurata MatConvNet, è necessario pre-elaborare i dati che utilizzeremo nell'addestramento. E' importante partire da una considerazione: i dati devono essere sufficienti all'addestramento, bilanciati, e strutturati in una maniera ben precisa.
Il numero di dati, infatti, deve essere sufficiente a permettere all'algoritmo di addestramento della nostra rete di regolarne adeguatamente i parametri (ossia pesi e bias). Inoltre, è importante che i dati non risultino tra loro sbilanciati, in quanto la rete potrebbe imparare a riconoscere in maniera ottimale solo un sottoinsieme degli oggetti presenti nel dataset di addestramento. Infine, è importante dare un'adeguata struttura ai dati, specificando anche le label che identificano le varie classi di dati presenti, e suddividendo adeguatamente gli insiemi di training e di validazione.
Nei nostri esperimenti, utilizzeremo il dataset creato da Andrea Vedaldi (l'autore di MatConvNet) a partire dal Google Fonts Project, ed addestreremo una semplice rete neurale per il riconoscimento dei caratteri. Osserviamone la struttura, caricandolo in memoria:
imdb = load(data/chardsb.mat) imdb.images ans = id: [1x29198 double] data: [32x32x29198 single] label: [1x29198 double] set: [1x29198 double]
Per prima cosa, notiamo un vettore degli id, che rappresenta gli identificativi di ciascuna delle 29198 immagini nel dataset. La matrice data, invece, contiene i dati veri e propri, ossia 29198 immagini di dimensioni 32 x 32; il vettore delle label, invece, rappresenta le etichette (o, per usare un formalismo più adeguato, le classi) di ciascuna delle immagini rappresentate. Vedaldi, nella struttura, inserisce anche un vettore set, che assume valore pari ad 1 qualora l'immagine sia utilizzata nell'addestramento della CNN, e pari a 2 qualora questa sia utilizzata per la validazione. E' interessante notare come questa non sia l'unica maniera di organizzare i dati da passare alla CNN: ad esempio, MathWorks suggerisce l'utilizzo della funzione imageDatastore, che crea una struttura simile a quella definita nel nostro esempio, e che permette di bilanciare i dati, e suddividerli in insiemi di training e validazione, a partire dalle loro label.
Creiamo la nostra prima CNN
Una volta terminato il setup della libreria e la pre-elaborazione dei dati, creiamo una funzione di inizializzazione della CNN, nella quale inseriremo i layer che compongono la nostra rete che, in questo esempio, sarà una SimpleNN. Una nota: vi sono precisi criteri per modificare i parametri dei singoli layer della rete, che non mostreremo in questa sede: di conseguenza, 'giocate' con attenzione!
Detto questo, inizializziamo la nostra rete:
net.layers = {};
L'intera rete è organizzata come un cell array, nel quale l'i-mo elemento è una struct contenente una serie di coppie chiave-valore rappresentative delle informazioni dell'i-mo layer della rete. Aggiungiamo, per prima cosa, un layer di convoluzione:
net.layers{end+1} = struct('name', 'conv1', ...
'type', 'conv', ...
'weights', {{randn(5,5,1,10,'single'), randn(1,10,'single')}}, ...
'stride', 1, ...
'pad', 0);
Osserviamo con attenzione la precedente struttura: abbiamo inserito, in coda al cell array layers, una struct, in cui la chiave name rappresenta il nome dato all'i-mo layer, il cui tipo è conv (chiaramente, convoluzionale), con un vettore dei pesi e dei bias indicato in weights, passo (stride) pari ad 1, e padding dell'immagine pari a 0. E' estremamente importante sottolineare che è necessario mantenere la coerenza dimensionale dei pesi e delle dimensioni delle matrici in ingresso: non potremo, ad esempio, avere vettori un numero complessivo di pesi differente dal numero di bias, così come è necessario che i filtri abbiano dimensione coerente con il numero di canali delle immagini in ingresso alla rete (in questo caso, essendo immagini in bianco e nero, si parla di un unico canale). In coda al layer di convoluzione, inseriamo un layer di pooling:
net.layers{end+1} = struct('name', 'max_pool1', ...
'type', 'pool', ...
'method', 'max', ...
'pool', [2 2], ...
'stride', 2, ...
'pad', 0);
In questo caso, la sintassi differisce leggermente nella specifica della chiave method, in questo caso max (che sta per max-pooling), e nell'indicazione dell'intorno su cui effettuare il pooling (in questo caso, una matrice quadrata di dimensioni 2 x 2). Il prossimo layer è una ReLU, la cui sintassi è estremamente semplice:
net.layers{end+1} = struct('name', 'relu1', ...
'type', 'relu');
Volendo, possiamo aggiungere altri strati di convoluzione/pooling/attivazione; in coda, però, ricordiamoci di inserire un layer completamente connesso, con funzione di attivazione softmax, che ci permetterà di 'binarizzare' l'output proveniente dalla rete, andando a dare una decisione 'hard' (sì o no) riguardo l'appartenenza, o meno, di un oggetto ad una determinata classe:
net.layers{end+1} = struct('type', 'softmaxloss');
L'ultima istruzione da chiamare nella nostra fucntion è vl_simplenn_tidy, che 'formatta' la rete rendendola compatibile con l'ultima versione disponibile di MatConvNet, allo scopo di evitare incongruenze e conflitti:
net = vl_simplenn_tidy(net);
Per inizializzare la nostra CNN, quindi, ci basterà chiamare la funzione initCnn dallo script principale. Una volta fatto questo, passiamo all'addestramento vero e proprio; sfrutteremo, in tal senso, la funzione cnn_train di MatConvNet, che mette a disposizione un metodo di training basato sull'algoritmo SGD (Stochastic Gradient Descent). Prima di procedere, però, occorre effettuare ancora un paio di operazioni.
[...]
ATTENZIONE: quello che hai appena letto è solo un estratto, l'Articolo Tecnico completo è composto da ben 2504 parole ed è riservato agli ABBONATI. Con l'Abbonamento avrai anche accesso a tutti gli altri Articoli Tecnici che potrai leggere in formato PDF per un anno. ABBONATI ORA, è semplice e sicuro.







ciao Angelo ottimo articolo, quante immagini di monete servirebbero per ri-addestrare la rete di Alexnet in maniera tale da aumentare il punteggio di similarità ottenuto?
Ciao Andrea, in generale, non c’è una risposta precisa alla tua domanda, ma vale il principio secondo cui ‘più ce n’è, meglio è’! In particolare, se volessi effettuare una procedura di transfer learning, con poche classi di monete (diciamo una decina), potresti ottenere buoni risultati anche con relativamente poche immagini (diciamo almeno un qualche centinaio). Se volessi addestrare da zero una rete apposita, ottenendo le stesse performance ottenibili da AlexNet, ci vorrebbero veramente molte immagini (pensa che ImageNet conta al suo interno circa 15 milioni di immagini).,