Dalla famiglia di microcontrollori PIC10F fino ai più potenti e versatili dsPIC, ecco le principali routine matematiche che consentono di fare dei microcontrollori Microchip delle vere macchine per il calcolo e l’analisi matematica.
Per chi lavorando con un microcontrollore Microchip della famiglia PIC16 si è trovato di fronte al problema di dover eseguire una moltiplicazione o una divisione ecco uno strumento applicativo per poter far uso di routine efficienti e bugs free.
Le routine di Somma e Differenza
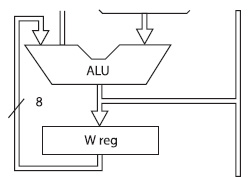
I pionieri della programmazione su Microchip, ossia coloro i quali per primi iniziarono a sviluppare sui PIC16C54, di certo si chiesero come fare ad implementare le operazioni di calcolo sui dati letti e acquisiti dal loro PIC. Per quanto riguarda la somma i microcontrollori della famiglia PIC16 sono dotati di un modulo hardware integrato nel silicio della ALU, come da figura 1.
Le routine di somma con risultato [-128…+127]
Le macchine ad 8 bit, per loro natura, riescono ad elaborare un solo byte di informazioni per volta, per cui ad esempio è possibile effettuare una somma fra due addendi ad 8 bit, o un confronto fra due valori ad 8 bit. Nel microcontrollore, come è noto, le informazioni sono espresse in formato binario, per cui ogni operazione che utilizza un operando di un byte può al massimo gestire il valore numerico decimale 255. Vi sono però casi in cui può essere interessante avere a disposizione valori che non siano compresi nell’intervallo decimale [0…+255]. Si pensi ad esempio all’uscita di un sensore differenziale, in cui il punto di riposo è lo 0 e le informazioni assumono significato diverso a seconda che siano maggiori o minori di 0. In questo caso potrebbe essere interessante far uso di una scala di valori diversa, magari centrata attorno allo 0, ad esempio [-128…+127]. Per poter fare uso di questa scala di valori, però, si rende necessario codificare l’informazione di segno, che invece non era necessaria nella rappresentazione [0…+255]. Per fare questo si utilizza una tecnica analitica denominata complemento a 2.
| Matematica binaria, il complemento a 2 di un numero
I numeri binari di un microcontrollore ad 8 bit, se interpretati senza segno vanno da: a 0000-0000 pari a decimale 0 a 1111-1111 pari a decimale 255 È però possibile interpretare diversamente questi 8 bit di informazione, facendo uso della matematica in complemento a due, in questo caso il primo bit rappresenta il segno e i successivi 7 bit rappresentano invece la mantissa del numero. Chiaramente il valore rappresentabile si riduce, perché un bit è impiegato per il segno. I numeri positivi compreso lo 0 hanno il primo bit a 0 e poi i successivi 7 rimangono immutati, come nella rappresentazione senza segno. Ad esempio:
Per i numeri negativi invece cambia il discorso, infatti se il numero è negativo il suo complemento a due vale il suo modulo (valore assoluto) negato e poi sommato ad uno. Ad esempio:
uno in prima posizione, per il segno negativo, poi la mantissa di 58 vale 0111010. Questo valore, come detto, deve essere negato, quindi si ottiene 1000101 e per finire, si deve eseguire la somma di uno, ottenendo la mantissa 1000110. Il numero finito col segno è quello trovato prima, di conseguenza. |
Nell’esempio precedente i valori +35 e –58 sono stati trasformati da notazione “unsigned” a notazione in complemento a due. Quest’ultima nasce appunto nell’ottica di poter eseguire operazioni su numeri con valore minore di zero, quindi eseguire somme e sottrazioni in maniera indifferente. Volendo ad esempio eseguire l’operazione (35-58), si tratta di eseguire la somma fra il numero decimale +35 e il numero decimale –58. Si veda l’operazione nel riquadro di approfondimento.
| Matematica binaria, la somma in complemento a 2
La somma fra il valore +35 e –58 si esegue nel seguente modo:
Si esegue la somma algebrica dei due, come se si trattasse di una normalissima somma fra numeri binari
Fatto questo, si prende il valore del risultato e, se è maggiore di zero (quindi se presenta un uno come prima cifra) non si fa altro che leggere il risultato, se invece è minore di zero (ossia presenta un 1 come prima cifra, come nel nostro caso) si inizia memorizzando il segno negativo e quindi si va a complementare tutta la mantissa da destro verso sinistra a partire da dopo il primo 1 che si incontra, quindi in questo caso si ha 000010111, pari proprio a 23, che va considerato col segno negativo. |
Questo dunque è, come appare chiaro, il metodo per implementare somme con numeri negativi ed anche le differenze! Nel listato 1 si riporta un algorito in grado di eseguire questo calcolo, che in caso di risultato eccedente i limiti [-128…+127] genera una saturazione del risultato.
;*******************************************
; Somma di due addendi con limitazione
; a +127 e a -128
; AARGB0 + AARGB1 = AARGB0
;*******************************************
CALCOLA_SOMMA
MOVLW 0X80
SUBWF AARGB0, W
BTFSC STATUS, C ; Qui se il numero è maggiore o minore di 0
GOTO AGGIUNGI_NEG
AGGIUNGI_POS
MOVLW 0X80
SUBWF AARGB1, W
BTFSC STATUS, C
GOTO POS_NEG
MOVF AARGB1, W ; Somma fra due positivi
ADDWF AARGB0, F
MOVLW 0X80
SUBWF AARGB0, W
BTFSS STATUS, C
RETURN
MOVLW 0X7F ; Saturazione della somma a +127
MOVWF AARGB0
RETURN
POS_NEG
MOVF AARGB1, W
ADDWF AARGB0, F
RETURN
AGGIUNGI_NEG
MOVLW 0X80
SUBWF AARGB1, W ; Complemento a 2
BTFSS STATUS, C
GOTO POS_NEG
MOVF AARGB1, W
ADDWF AARGB0, F
MOVLW 0X80
SUBWF AARGB0, W
BTFSC STATUS, C
RETURN
MOVLW 0X80 ; Saturazione a -128
MOVWF AARGB0
RETURN
| Listato 1 |
È interessante notare che Microchip ha fissato dei nomi specifici per denominare gli addendi e i fattori delle sue routine matematiche, per far sì che queste possano coesistere senza creare interferenze le une con le altre, ma anzi consentendo possibili interazioni fra diversi algoritmi. Nel caso della somma, Microchip denomina i due addendi AARGB0 e AARGB1, mentre il risultato viene scritto su AARGB0, sovrascrivendo di conseguenza il primo addendo.
Le routine di somma con risultato a 16 bit
In alcune applicazioni particolarmente specifiche dal punto di vista dell’analisi matematica, il limite fissato da una aritmetica a byte potrebbe non essere sufficiente. Potrebbero quindi non bastare i risultati compresi fra i valori decimali [-128…+127] oppure [0…+255]. Le tecniche firmware nella programmazione dei PIC consentono però di superare questo ostacolo, potendo infatti realizzare delle operazioni che considerino due registri ad 8 bit come un unico corpo a 16 bit, facendo uso delle istruzioni di shift a sinistra e a destra. Nel listato 2 l’esempio della somma e della differenza a 16 bit.
;******************************************************************* ; Double Precision Addition ; ; Addition : ACCb(16 bits) + ACCa(16 bits) -> ACCb(16 bits) ; (a) Load the 1st operand in location ACCaLO & ACCaHI ( 16 bits ) ; (b) Load the 2nd operand in location ACCbLO & ACCbHI ( 16 bits ) ; (c) CALL D_add ; (d) The result is in location ACCbLO & ACCbHI ( 16 bits ) ; ; Performance : ; Program Memory : 4 (excluding call & return) ; Clock Cycles : 4 (excluding call & return) ; W Register : Used ; Scratch RAM : 0 ; ;*******************************************************************; ; D_add movfp ACCaLO,WREG addwf ACCbLO, F ;addwf lsb movfp ACCaHI,WREG addwfc ACCbHI, F ;addwf msb with carry return ; ;*******************************************************************; ;******************************************************************* ; Double Precision Subtraction ; ; Subtraction : ACCb(16 bits) - ACCa(16 bits) -> ACCb(16 bits) ; (a) Load the 1st operand in location ACCaLO & ACCaHI ( 16 bits ) ; (b) Load the 2nd operand in location ACCbLO & ACCbHI ( 16 bits ) ; (c) CALL D_sub ; (d) The result is in location ACCbLO & ACCbHI ( 16 bits ) ; ; Performance : ; Program Memory : 4 (excluding call & return ) ; Clock Cycles : 4 (excluding call & return ) ; W Register : Used ; scratch RAM : 0 ;*******************************************************************; ; D_sub movfp ACCaLO,WREG subwf ACCbLO, F movfp ACCaHI,WREG subwfb ACCbHI, F return ;*******************************************************************;
| Listato 2 |
Le routine di Moltiplicazione e Divisione
Le routine di moltiplicazione 8x8 con segno e con risultato ad 8 bit
Come visto, la routine matematica CALCOLA_SOMMA consente di realizzare una operazione matematica appoggiandosi ad una aritmetica binaria particolare e facendo uso di alcuni stratagemmi consentiti dall’architettura del microcontrollore. Nel caso della moltiplicazione, invece, si fa un uso molto più pesante degli algoritmi e delle istruzioni del microcontrollore, impostando invece il calcolo su principi aritmetici molto meno “sofisticati”. La moltiplicazione, infatti, viene vista come un ciclo “Repeat…until” che aggiunge a se stesso il primo addendo tante volte quante sono il numero rappresentato dal secondo addendo. Per la somma si fa uso proprio della routine CALCOLA_SOMMA appena studiata. La possibilità di far uso dei numeri negativi fa sì che uno dei due addendi possa essere negativo. Nella pratica, Microchip ha riservato due codici mnemonici per i registri fattori, AARGB5 e BARGB5, con risultato ad 8 bit che viene sovrascritto a AARGB5. Si sfruttano poi alcuni registri di appoggio, per mettere in temporaneo salvataggio i risultati delle somme parziali citate precedentemente. Uno di questi è AARGB0, che funge sempre da registro temporaneo nelle routine matematiche, ragion per cui può essere utilizzato senza problemi sia in questa routine che nella CALCOLA_SOMMA, che come detto viene chiamata ricorsivamente dalla MOLTIPLICA. I due fattori saranno dunque compresi nel range [0…255] per il fattore senza segno e [-128…+127] per quello con segno. Nel listato 3 la routine.
;*******************************************;
; Moltiplicazione 8x8 con segno ;
; (solo un operando può essere negativo) ;
; AARGB5 * BARGB0 = AARGB5 ;
;*******************************************;
MOLTIPLICA
MOVF BARGB0, W
MOVWF COUNT_MUL
BTFSC STATUS, Z
GOTO MUL_NULL
MOVF AARGB5, W
MOVWF AARGB0
MOVWF AARGB1
LOOP1
DECFSZ COUNT_MUL,F
GOTO MUL
MOVF AARGB0, W
MOVWF AARGB5
RETURN
MUL
CALL CALCOLA_SOMMA
GOTO LOOP1
MUL_NULL
CLRF AARGB5
RETURN
| Listato 3 |
Le routine di moltiplicazione 8x8 senza segno e con risultato a 16 bit
Un’altra routine di sicuro interesse ed utilità è la moltiplicazione senza segno fra due valori ad 8 bit, con risultato a 16 bit. Sarà quindi possibile moltiplicare fra loro fattori compresi nel range [0…255] ottenendo un risultato compreso nel range [0…65535]. Tramite questa operazione sarà quindi possibile, per la prima volta, uscire dal limite imposto da una aritmetica a byte, ossia da 28=256. Si può infatti rappresentare il massimo numero consentito da due byte, ossia 216-1=65535. Questo risultato è possibile solamente grazie allo shifting dell’MSB (Most Significant Bit) del byte meno significativo nell’LSB (Least Significant Bit) del byte più significativo, passando come riporto attraverso il carry bit del registro STATUS (figura 2).
Utilizzando questo bit quale “registro di appoggio”, è possibile mettere in cascata i due registri, facendo sì che essi possano esser visti ed utilizzati come un unico registro a 16 bit. Anche per questa routine si fornisce il codice nel listato 4.
;*******************************************;
; Moltiplicazione 8x8 senza segno
; risultato in 16 bit ( MSB=AARGB0 )
; AARGB0*BARGB0=AARGB0,AARGB1
;*******************************************;
FXM0808U
CLRF AARGB1
MOVLW 0x08
MOVWF LOOPCOUNT ;Numero di rotazioni necessarie
MOVF AARGB0,W
LOOPUM0808A
RRF BARGB0, F
BTFSC STATUS, C
GOTO LUM0808NAP
DECFSZ LOOPCOUNT, F
GOTO LOOPUM0808A
CLRF AARGB0
RETLW 0x00
LUM0808NAP
BCF STATUS, C
GOTO LUM0808NA
LOOPUM0808
RRF BARGB0, F
BTFSC STATUS, C
ADDWF AARGB0, F
LUM0808NA
RRF AARGB0, F
RRF AARGB1, F
DECFSZ LOOPCOUNT, F
GOTO LOOPUM0808
RETLW 0x00
| Listato 4 |
Le routine di divisione 8x8 con segno e con risultato a 8 bit
Certamente, fra tutte le routine matematiche, la più complessa da rappresentare in una macchina a 8 bit senza blocco moltiplicatore hardware è proprio la divisione. Il motivo di questa difficoltà sta nel fatto che si devono fare moltiplicazioni, some e confronti fra il secondo fattore ed il primo: in pratica invece di considerare una divisione Y=a/b si considera un confronto ricorsivo fra a e il numero di volte in cui b può essere contenuto in a. Nel listato 5 la procedura, abbastanza pesante, ma ottimizzata. Importante notare che uno dei due valori AARGB0 o BARGB0 può avere segno negativo, conferendo così all’operazione la possibilità di lavorare con operandi relativi.
;*******************************************;
; Routine di divisione 8x8 con segno ;
; AARGB0 : BARGB0 = AARGB0 ;
;*******************************************;
FXD0808S
CLRF SIGN
CLRF REMB0
MOVF AARGB0, W
BTFSC STATUS, Z
RETLW 0x00
XORWF BARGB0, W
MOVWF TEMP
BTFSC TEMP, MSB
COMF SIGN, F
CLRF TEMPB3
BTFSS BARGB0, MSB
GOTO CA0808S
COMF BARGB0, F
INCF BARGB0, F
CA0808S
BTFSS AARGB0, MSB
GOTO C0808SX
COMF AARGB0, F
INCF AARGB0, F
C0808SX
MOVF AARGB0, W
IORWF BARGB0, W
MOVWF TEMP
BTFSC TEMP, MSB
GOTO C0808SX1
C0808S
MOVF BARGB0, W
SUBWF REMB0, F
RLF AARGB0, F
RLF AARGB0, W
RLF REMB0, F
MOVF BARGB0, W
ADDWF REMB0, F
RLF AARGB0, F
MOVLW .6
MOVWF LOOPCOUNT
LOOPS0808A
RLF AARGB0, W
RLF REMB0, F
MOVF BARGB0, W
BTFSC AARGB0, LSB
SUBWF REMB0, F
BTFSS AARGB0, LSB
ADDWF REMB0, F
RLF AARGB0, F
DECFSZ LOOPCOUNT,F
GOTO LOOPS0808A
BTFSS AARGB0, LSB
ADDWF REMB0, F
BTFSC TEMPB3, LSB
GOTO C0808SX4
C0808SOK
BTFSS SIGN, MSB
RETLW 0x00
COMF AARGB0, F
INCF AARGB0, F
COMF REMB0, F
INCF REMB0, F
RETLW 0x00
C0808SX1
BTFSS BARGB0, MSB
GOTO C0808SX3
BTFSC AARGB0, MSB
GOTO C0808SX2
MOVF AARGB0, W
MOVWF REMB0
CLRF AARGB0
GOTO C0808SOK
C0808SX2
CLRF AARGB0
INCF AARGB0, F
RETLW 0x00
C0808SX3
COMF AARGB0, F
INCF TEMPB3, F
GOTO C0808S
C0808SX4
INCF REMB0, F
MOVF BARGB0, W
SUBWF REMB0, W
BTFSS STATUS, Z
GOTO C0808SOK
CLRF REMB0
INCF AARGB0, F
BTFSS AARGB0, MSB
GOTO C0808SOK
RETLW 0xFF
| Listato 5 |
Le routine di divisione 16x8 senza segno e con risultato a 16 bit
Si consegna all’analisi dei lettori la divisione fra valori senza segno a 16 bit, quindi compresi nel range [0…65535]. Il risultato sarà dunque un valore a 16 bit. Il listato 6 riporta la routine completa.
;******************************************************************* ; Double Precision Division ; ; ( Optimized for Code : Looped Code ) ; ;*******************************************************************; ; Division : ACCb(16 bits) / ACCa(16 bits) -> ACCb(16 bits) with ; Remainder in ACCc (16 bits) ; (a) Load the Denominator in location ACCaHI & ACCaLO ( 16 bits ) ; (b) Load the Numerator in location ACCbHI & ACCbLO ( 16 bits ) ; (c) CALL D_div ; (d) The 16 bit result is in location ACCbHI & ACCbLO ; (e) The 16 bit Remainder is in locations ACCcHI & ACCcLO ; ; Performance : ; Program Memory : 31 (UNSIGNED) ; 39 (SIGNED) ; Clock Cycles : 300 (UNSIGNED : excluding CALL & RETURN) ; : 312 (SIGNED : excluding CALL & RETURN) ; ; NOTE : ; The performance specs are for Unsigned arithmetic ( i.e, ; with “SIGNED equ FALSE “). ; ;******************************************************************* ; Double Precision Divide ( 16/16 -> 16 ) ; ; ( ACCb/ACCa -> ACCb with remainder in ACCc ) : 16 bit output ; with Quotiont in ACCb (ACCbHI,ACCbLO) and Remainder in ACCc (ACCcHI,ACCcLO). ; ; B/A = (Q) + (R)/A ; or B = A*Q + R ; ; where B : Numerator ; A : Denominator ; Q : Quotiont (Integer Result) ; R : Remainder ; ; Note : Check for ZERO Denominator or Numerator is not performed ; A ZERO Denominator will produce incorrect results ; ; SIGNED Arithmetic : ; In case of signed arithmetic, if either ; numerator or denominator is negative, then both Q & R are ; represented as negative numbers ; -(B/A) = -(Q) + (-R)/A ; or -B = (-Q)*A + (-R) ; ;******************************************************************* ; D_divS ; bsf ALUSTA,FS0 bsf ALUSTA,FS1 ; set no auto-incrment for fsr0 #if SIGNED CALL S_SIGN #endif ; clrf count, F bsf count,4 ; set count = 16 clrf ACCcHI, F clrf ACCcLO, F clrf ACCdLO, F clrf ACCdHI, F ; ; Looped code ; divLoop bcf ALUSTA,C rlcf ACCbLO, F rlcf ACCbHI, F rlcf ACCcLO, F rlcf ACCcHI, F movfp ACCaHI,WREG subwf ACCcHI,W ; check if a>c btfss ALUSTA,Z goto notz movfp ACCaLO,WREG subwf ACCcLO,W ; if msb equal then check lsb notz btfss ALUSTA,C ; carry set if c>a goto nosub ; if c < a subca movfp ACCaLO,WREG ; c-a into c subwf ACCcLO, F movfp ACCaHI,WREG subwfb ACCcHI, F bsf ALUSTA,C ; shift a 1 into d (result) nosub rlcf ACCdLO, F rlcf ACCdHI, F decfsz count, F goto divLoop ; #if SIGNED btfss sign,MSB return movlw ACCcLO movwf fsr0 call negate movlw ACCdLO movwf fsr0 call negate return
| Listato 6 |
Le routine floating point per il calcolo di funzioni trigonometriche
A completare il quadro delle routine aritmetiche ad 8 e 16 bit, ecco una breve panoramica delle funzionalità trigonometriche, rese possibili dall’utilizzo di una aritmetica che prevede l’uso della virgola. Per chi non ricorda più le pagine dei testi di trigonometria, sfogliate così tante volte durante i corsi di studi, si ricorda che la funzione Seno(x) assume valori compresi nel range [-1..1], motivo per cui sarà necessario poter far uso del concetto di virgola. Angoli vicini allo 0, poi, danno origine a valori del seno prossimi allo 0. In alcune applicazioni lo studio si focalizza attorno ad un range molto ristretto in gradi, per cui non è detto a priori quale deve essere la posizione della virgola all’interno della mantissa, sia quest’ultima un valore a 16, 24 o 32 bit. Se, ad esempio, vogliamo considerare valori in gradi compresi fra [0°…10°], come nel caso di un braccio robotico per automazione industriale, avremo a che fare con valori del seno compresi nel range [0…0,1736482]. Ecco che dunque sarà utile tenere la virgola nella prima posizione disponibile dopo il primo valore intero. Se invece si tratta della funzione arcoseno, ossia si deve trovare l’arco cui corrisponde un determinato valore del seno, si avranno operandi simili a quello appena trattato, ma risultato con due o tre cifre intere (da 0 a 360 gradi). Questo rende evidente la necessità di operare con valori in cui la posizione della virgola non è nota a priori. Questi valori assumono in analisi numerica il nome di Floating Point. Nel listato 7 si fornisce la funzione per il calcolo del seno di un valore a 16 bit, in cui i primi 8 bit rappresentano l’esponente cui elevare la successiva mantissa a 16 bit.
;**************************************************************************************** ; Evaluate sin(x) ; Input: 24 bit floating point number in AEXP, AARGB0, AARGB1 ; Use: CALL SIN24 ; Output: 24 bit floating point number in AEXP, AARGB0, AARGB1 ; Result: AARG <-- SIN( AARG ) ; Testing on [-LOSSTHR,LOSSTHR] from 100000 trials: ; min max mean ; Timing: 2564 4494 4134.5 clks ; min max mean rms ; Error: -0x56 0x13 -7.12 20.89 nsb ;---------------------------------------------------------------------------------------- ; The actual argument x on [-LOSSTHR,LOSSTHR] is mapped to the ; alternative trigonometric argument z on [-pi/4,pi/4], through ; the definition z = x mod pi/4, with an additional variable j ; indicating the correct octant, leading to the appropriate call ; to either the sine or cosine approximations ; sin(z) = z * p(z**2),cos(z) = q(z**2) ; where p and q are minimax polynomial approximations. SIN24 MOVF FPFLAGS,W ; save rounding flag MOVWF DARGB3 BCF FPFLAGS,RND ; disable rounding CLRF CARGB3 ; initialize sign in CARGB3 BTFSC AARGB0,MSB ; toggle sign if x < 0 BSF CARGB3,MSB BCF AARGB0,MSB ; use |x| CALL RRSINCOS24 RRSIN24OK RRF EARGB3,W XORWF EARGB3,W MOVWF TEMPB0 BTFSC TEMPB0,LSB GOTO SINZCOS24 CALL ZSIN24 GOTO SINSIGN24 SINZCOS24 CALL ZCOS24 SINSIGN24 MOVLW 0x80 BTFSC CARGB3,MSB XORWF AARGB0,F BTFSS DARGB3,RND RETLW 0x00 BSF FPFLAGS,RND ; restore rounding flag CALL RND3224 RETLW 0x00
| Listato 7 |
Le routine nelle famiglie superiori alla 16
Le formule matematiche che possono risultare utili in implementazioni elettroniche potrebbero essere innumerevoli, com’è chiaro. Certamente, però, poter disporre delle quattro operazioni fondamentali dell’aritmetica aiuta a poter eseguire praticamente ogni tipo di implementazione più complessa. Speriamo che questo articolo possa essere di aiuto quale guida pratica alle implementazioni analitiche nella famiglia più difficoltosa da questo punto di vista, ossia la 16. Si tenga presente, infatti, che la famiglia 16, essendo dotata del solo sommatore hardware, risulta la più complessa su cui costruire operazioni matematiche.
Il moltiplicatore Hardware nei PIC18
I microcontrollori della famiglia PIC18C,Fxxx sono dotati di un moltiplicatore hardware interno, consentendo quindi un notevole potenziamento nelle operazioni matematiche rispetto alla famiglia 16. Il modulo, in pratica, è in grado di eseguire una moltiplicazione fra valori senza segno ad 8 bit e tenere memoria del risultato nei registri PRODH e PRODL, rispettivamente per la parte più significativa e meno significativa, che è chiaramente a 16 bit. Questa operazione viene eseguita in un unico ciclo macchina. Eccone un esempio:
MOVF ARG1, W MULWF ARG2 ; ARG1 * ARG2 -> ; PRODH:PRODL BTFSC ARG2, SB ; Test Sign Bit SUBWF PRODH, F ; PRODH = PRODH ; - ARG1 MOVF ARG2, W BTFSC ARG1, SB ; Test Sign Bit SUBWF PRODH, F ; PRODH = PRODH ; - ARG2
Per quanto concerne le famiglie superiori, la 18 ha il modulo moltiplicatore hardware, per cui le moltiplicazioni possono essere eseguite in un unico ciclo macchina dall’hardware. Si veda nella tabella di figura 3 un confronto fra i tempi di calcolo nel caso di utilizzo del moltiplicatore hardware e nel caso invece di una moltiplicazione eseguita per intero via Firmware. Per finire, i nuovi dsPIC sono dotati di moltissime periferiche e strutture interne hardware dedicate all’analisi matematica, non ultimo il Barrel Shifter, tramite il quale è possibile effettuare non solo MAC (Multiply and Accumulate) in un unico ciclo macchina, ma perfino una FFT (Fast Fourier Transofrm, o Trasformata di Fourier tempo discreta). Queste performance di tutto rispetto sono possibili grazie ad alcuni accorgimenti hardware specifici per l’esecuzione di routine matematiche ad alta ottimizzazione. Oltre al citato barrel shifter, sono presenti infatti due registri Accumulatori a 40 bit (AccuX e AccuY), che sono condivisi dalla ALU standard e dal core DSP e che consentono di realizzare e gestire in un unico ciclo macchina l’operazione Y=ax+b, che è proprio la citata operazione di MAC. Oltre a questo, i due accumulatori possono essere programmati per la gestione automatizzata dei dati in ingresso e in uscita, per poter creare una sorta di FIFO virtuale. Grazie a questa caratteristica si possono realizzare con facilità i citati Filtri Digitali, dal momento che i dati x possono essere combinati ai coefficienti a e b in maniera del tutto automatizzata. Molte altre sono le possibilità offerte da questi microcontrollori di alta gamma Microchip, ma si lasciano ai prossimi numeri ulteriori approfondimenti.


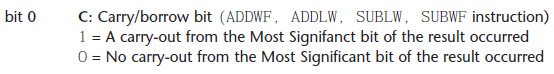




Ottimo articolo. In passato ho utilizzato questa tecnica per calcolare la percentuale di un valore letto in frequenza tramite un PIC 12F675. Tutti questi bei articoli, in ASM, verranno poi riuniti in un numero speciale?
Potrebbe essere una buona idea 😉
Fantastico articolo in ASM in rete in questo anno 2025 si trovano pochissimi esempi scritti in ASM, scritti solo in C oppure C++ gli esempi mi sono stati di grandissimo aiuto io di solito utilizzavo calcoli ad 8 bit….. Grazie di tutto, lo condividerò a tante persone