L'elaborazione digitale dei segnali consente di ottenere risultati di gran lunga superiori a quelli che si avrebbero con un'elaborazione analogica. In quest'ambito hanno riscosso grande successo i DSP, utilizzati ormai nei più svariati campi applicativi, tra cui audio e video. Nell'articolo si analizzerà una particolare famiglia di Digital Signal Processor prodotti della Analog Devices: gli Sharc.
Un DSP (Digital Signal Processor) ha il compito di acquisire segnali del “mondo reale” come voce, audio, video ed altri parametri analogici, digitalizzarli, manipolarli tramite opportune operazione e quindi restituirli nel dominio analogico. Un DSP è progettato per eseguire funzioni matematiche come addizione, sottrazione, moltiplicazione e divisione a velocità molto maggiori rispetto ai normali microprocessori. Un schema di principio della tipica architettura di un DSP è riportato in figura 1.

Figura 1: Un DSP ha il compito di acquisire tramite ADC un segnale analogico, modificarlo e restituirlo in forma analogica tramite un DAC.
Il primo DSP monolitico lanciato nel 1978 sul mercato fu l’Intel 2920 dotato di ALU priva di moltiplicatore ed una architettura Harvard VLIW (Very Long Instruction Word) di 24 bit immagazzinata su 192 locazioni di EPROM, uno spazio di RAM di 40 parole da 25 bit ed interfacce ADC e DAC a bordo. Ogni DSP è quindi adatto ad applicazioni specifiche: ad esempio, i DSP a 16-bit a virgola fissa sono impiegati per il condizionamento di segnali vocali e trovano il loro principale campo di applicazione nella telefonia (fissa e mobile), mentre i DSP a 32-bit in virgola mobile, poiché dotati una dinamica superiore, sono principalmente impiegati nell’elaborazione di immagini e nella grafica tridimensionale. Tra i principali campi di applicazione di un DSP si possono citare:
➤ Tecnologie spaziali: miglioramento delle fotografie, compressione dei dati, analisi intelligente dei dati ricevuti dai sensori.
➤ Medicina: diagnosi tramite immagini (CT, MRI, Ultrasuoni, e altri), elettrocardiogramma.
➤ Commercio: compressione dei suoni e delle immagini, effetti speciali, videoconferenze.
➤ Telefonia: compressione dati e voce, riduzione eco, multiplexing, filtraggio disturbi.
➤ Militare: radar, sonar, comunicazioni sicure.
➤ Industrie: monitoraggio risorse petrolifere, disegno CAD.
➤ Scientifico: analisi terremoti, acquisizione dati, analisi spettrali, simulazioni.
➤ Multimedia: compressione/decompressione e trattamento audio-video, strumenti musicali digitali e software di elaborazione audio, computer music
Il modulo MAC nei processori SHARC
L’operazione MAC
Molto spesso l’elaborazione di dati digitalizzati prevede l’utilizzo intensivo di operazioni semplici come la somma e la moltiplicazione. Generalmente, tali operazioni sono eseguite in combinazione. Si tratta della tipica operazione di un DSP: il MAC (Multiply and ACcumulate). Essa si può riassumere come segue:
a ← a + b × c
si tratta cioè di moltiplicare due numeri ed accumularli in un’unica variabile. Per esempio, l’operazione di convoluzione è molto utilizzata nell’analisi d’immagini e nella grafica, soprattutto per operazioni di filtraggio nei sistemi lineari tempo-invarianti. Fare la convoluzione di due segnali significa moltiplicare i relativi spettri nel dominio della frequenza e si può definire (nel dominio del tempo):
f * g (m) = ∑N f(n) g(m-n)
Come si può facilmente notare, l’operazione di convoluzione richiede essenzialmente l’operazione di MAC dei DSP. L’unità di moltiplicazione del processori SHARC esegue sia operazioni in virgola mobile che fixed-point. Tale unità include le seguenti istruzioni:
➤ Moltiplicazione floating-poing
➤ Moltiplicazione fixed-point
➤ MAC con addizione
➤ MAC con sottrazione
➤ Arrotondamento (rounding) del registro risultato
➤ Saturazione (saturating) del registro risultato
➤ Azzeramento (clearing) del registro risultato
Il registro utilizzato per memorizzare il risultato è il Multiplier Result (MRF), su tale registro posso essere eseguite anche le operazione di rounding, saturating e clearing. L’operazione è eseguita in un solo ciclo di clock. Lo schema a blocchi del moltiplicatore è illustrato in figura 2.
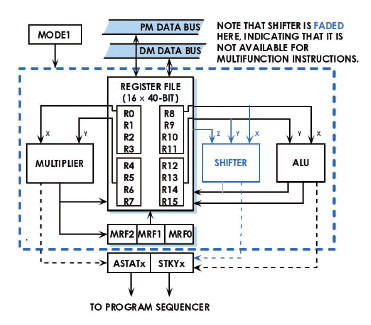
Figura 2: schema del moltiplicatore/accumulatore presente nel processore SHARC.
L’operazione di moltiplicazione aggiorna i flag di stato dei registri ASTATx e ASTATy, come descritto in figura 3.
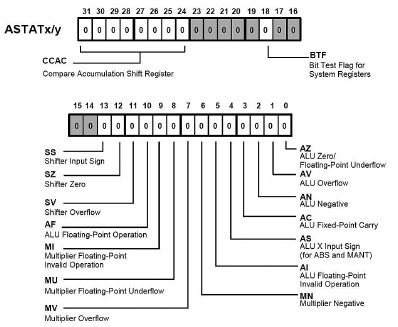
Figura 3: flag aggiornati durante un’operazione di moltiplicazione.
Il listato 1 riporta un semplice routine di esempio (che può anche essere inclusa in altri sorgenti) per eseguire la moltiplicazione/accumulazione tra due vettori di numeri complessi.
/************************************************************** Nome file: Complex_Vector_Multiply_Accumulate.asm **************************************************************/ #include “def21262.h” /* Symbol Definition File */ .global cx_vec_mult_accum; /* program memory code */ .section/pm seg_pmco; cx_vec_mult_accum: /* Circular Buffer, SIMD enabled, Broadcast I1 & I9 enabled */ bit set MODE1 CBUFEN | PEYEN | BDCST1 | BDCST9; lcntr=r2, do macs until lce; /* F13/S13 = Xi*Yr, F12/S12 = Zr + Xr*Yr - Xi*Yi, F0/S0 = Xr(odd), /* F1/S1 = Xi(odd) , F4/S4 = Yr(even), F5/S5 = Yi(even) */ /* F0 = Xr(even), F1 = Xi(even), S4 = Yr(odd), S5 = Yi(odd) */ f13=f1*f4, f12=f8-f12,f0=dm(i1,m0),f4=pm(i9,m8);f0=dm(i0,m0),f4=pm(i8,m8); /* F8/S8 = Xr*Yr, F13/S13 = Zi + Xr*Yi + Xi*Yr, /* F14 = Zr(even), F15 = Zi(even) */ f8=f0*f4, f13=f10+f13, f14=dm(i2,m1); /* S14 = Zr(odd), S15 = Zi(odd) */ s14=dm(i2,m2); /* F10/S10 = Xr*Yi, F8/S8 = Xr*Yr + Zr, store results of even samples */ f10=f0*f5, f8=f8+f14, dm(i2,m1)=f12; /* F12/S12 = Xi*Yi, F10/S10 = Xr*Yi + Zi, store results of odd samples */ macs: f12=f1*f5, f10=f10+f15, dm(i2,m3)=s12; rts (db); /* Circular Buffer, SIMD disabled, Broadcast I1 & I9 disabled */ bit clr MODE1 CBUFEN | PEYEN | BDCST1 | BDCST9; nop;
| Listato 1 |
Per tale funzione sono utilizzati due vettori complessi (X e Y) ed un terzo per l’accumulazione. L’equazione implementata può essere così riassunta:
Z(n) = Z(n) + X(n)*Y(n)
Benchmark per processori SHARC
Le applicazioni basate sull’elaborazione di segnali in tempo reale richiedono elevata capacità computazionale. Nei processori SHARC, oltre alla progettazione di unità matematiche ad elevata velocità e di un core che esegua una istruzione per ciclo di clock, molta è stata riservata anche alla ottimizzazione della banda di memoria e alla velocità di accesso degli I/O. Quindi il bilanciamento tra velocità del core, integrazione della memoria e velocità degli I/O permettono di far fronte alle più critiche applicazioni real-time. In quest’ottica la caratterizzazione di un DSP tramite benchmark risulta di fondamentale importanza. Quasi sempre valutare parametri come MIPS o velocità del clock è limitante.




