Abbiamo già visto qualche applicazione di MATLAB e SIMULINK e dopo questi antipasti passiamo ad un esempio che ci mostra la filosofia di funzionamento di SIMULINK, in attesa della portata principale che arriverà nelle prossime puntate. Come suggerisce il nome, lo scopo di SIMULINK è la simulazione dei sistemi dinamici. Ma cosa è una simulazione? E cosa sono i sistemi dinamici? Lo scopriremo proprio oggi grazie ad un esempio classico, semplice ma completo: un circuito RC.
Forse non c’è bisogno di scomodare SIMULINK per simulare un circuito elettrico elementare ma è proprio la semplicità del circuito che ci permette di concentrarci sui meccanismi di simulazione, che sono poi anche alla base di tanti software di simulazione circuitale, nonchè sulle caratteristiche del circuito stesso e dei risultati da ottenere. L’obiettivo dell’analisi di un circuito è determinare come evolvono nel tempo le grandezze elettriche e per farlo dobbiamo scrivere (e risolvere!) le equazioni che descrivono la struttura del circuito stesso (come le leggi di Kirchhoff) e le relazioni costitutive dei componenti (legge di Ohm per le resistenze, 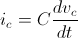 per i condensatori, ecc.).
per i condensatori, ecc.).
Consideriamo il circuito in figura:
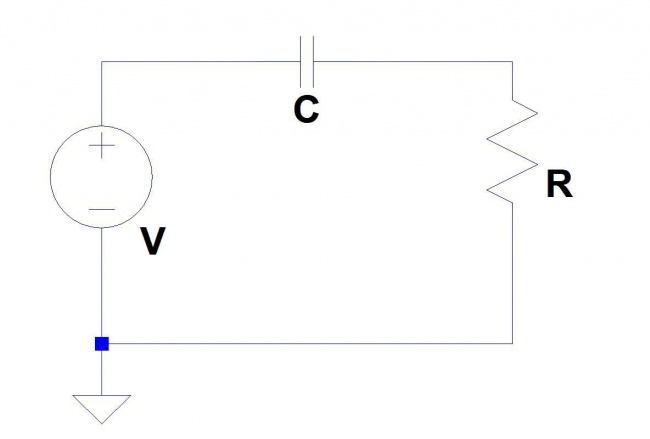
possiamo scrivere :
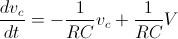
L’incognita vc (tensione sul condensatore) compare sotto il segno di derivata. Per determinarne l’evoluzione si può allora fare l’operazione inversa, cioè calcolare l’integrale di tutta l’espressione a destra. Magari per questa equazione può essere quasi facile da fare a mano se la V ha una espressione semplice (ad esempio una sinusoide a frequenza di rete) ma in generale non è così e allora SIMULINK ci viene in aiuto perché offre un blocco integratore: se si crea uno schema che riproduce l’espressione a destra allora il simulatore si fa carico di calcolare l’integrale. Lo schema che ne viene fuori si chiama schema di Lord Kelvin.
Naturalmente lo stesso procedimento si può estendere a casi più complessi: si usa un integratore per ogni componente, tipo condensatore o induttore, il cui legame corrente-tensione è definito per mezzo di una derivata e si collegano poi le variabili con sommatori e guadagni come nell’esempio che stiamo discutendo. Addirittura è possibile usare qualsiasi funzione matematica e questo ci permette di simulare anche sistemi “non lineari”, cosa non possibile con l’approccio basato su funzioni di trasferimento che, come noto, sono una rappresentazione di sistemi lineari!
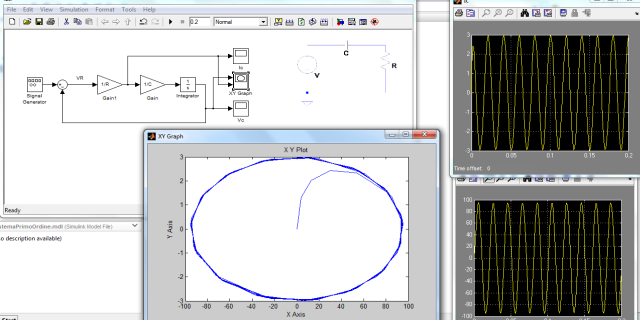
In figura è mostrato il modello che si ottiene:
Leggendo lo schema a blocchi da sinistra troviamo il generatore di segnali, un sommatore, due guadagni, l’integratore ed infine tre blocchi di visualizzazione. Il generatore è strutturato proprio come uno strumento virtuale, ci permette di selezionare diverse forme d’onda, l’ampiezza e la frequenza. Con il doppio click si apre una finestra di dialogo come quella riportata in figura:
Nel nostro esempio useremo una sinusoide a frequenza di rete (50 Hz).
Seguono i due guadagni. In realtà può essere sufficiente, ai fini della simulazione, anche un solo guadagno pari 1/(R*C) ma ho preferito tenerli separati per ricavare anche la corrente del condensatore e non solo la sua tensione. Notiamo come nei guadagni non ci siano dei valori numerici ma solo dei parametri il cui valore va preventivamente dichiarato in MATLAB (in caso contrario un messaggio di errore ci avvisa che non è possibile simulare!): questo ci consente di effettuare diverse simulazioni, semplicemente assegnando i diversi valori in MATLAB, senza dover modificare ogni volta il circuito.
Una ulteriore capacità di MATLAB è quella di simulare il sistema senza neanche aprire lo schema, ma semplicemente usando il comando sim:
%%% codice matlab
>> R=10;
>> C=100e-6;
>> sim('SistemaPrimoOrdine')
In questo caso occorre utilizzare dei metodi per passare i risultati di simulazione al workspace (l’ambiente di lavoro dove sono memorizzate le variabili di MATLAB). Un modo semplice è quello di configurare opportunamente i blocchi scope, come in figura:
Avere i dati nel workspace è utile per poter effettuare delle analisi sui dati (ricordiamo che gli scope consentono solo la visualizzazione del segnale in ingresso, con al massimo uno zoom) piuttosto che per salvarli in un opportuno file .mat in modo da archiviarli ed utilizzarli in seguito senza dover nuovamente simulare (provate a pensare ad un sistema che impiega qualche ora prima di fornire i dati ed apprezzerete questa opportunità!).
La sintassi del comando è:
save nomefile variabile1 variabile2
Nel nostro caso potremmo digitare
save risultati correnti tensioni
Ovviamente si possono memorizzare quante variabili si vuole. In particolare se si omettono i nomi delle variabili, si memorizza tutto il workspace, mentre per aggiungere una nuova variabile ad un file esistente si deve scrivere, dopo le variabili, -append (in caso contrario si cancellerà tutto quanto è presente nel file che risulterà contenere solo le ultime variabili scritte dopo save). Tornando allo schema SIMULINK vediamo che è presente anche un blocco “XY Graph” che si comporta, come suggerisce il nome, come un oscilloscopio in modalità X-Y, di cui abbiamo già parlato in un precedente articolo.
Abbiamo posto sull’asse X la tensione del condensatore e sull’asse Y la corrente: in questo modo è possibile misurare l’impedenza del condensatore usando le figure di Lissajous. In realtà questo blocco non ha le stesse funzionalità di uno scope, ad esempio non consente di salvare i segnali in ingresso e non fornisce strumenti di zoom, per questo in genere preferisco riportare i segnali in MATLAB e poi elaborarli (e, se serve, fare un plot “mirato” alle necessità).
Passiamo alle simulazioni e vediamo qualche risultato. Il generatore in ingresso simula un generatore di tensione (da cui discende la struttura delle equazioni che abbiamo commentato prima) di 100 V a 50Hz. La scelta non è casuale: l’ampiezza consente di semplificare i calcoli per una verifica "manuale", mentre la frequenza è quella di rete, in modo da dare al circuito anche un senso “pratico” (anche se io non userei mai un condensatore per ridurre la tensione su un carico, mi è capitato trovarlo in alcune “cineserie”!). I valori scelti sono: R=10 Ω e C=100 μF. Diamo un sguardo ai risultati. La corrente nel condensatore (e quindi nella resistenza) è mostrata nella figura seguente:
Si ha il valore massimo a circa 3 A, quindi possiamo dire che l’impedenza ha un modulo di 100/3 ≅ 33 Ω, coerente con quella teorica: 1/(2π*f*C)≅ 1/(314*C). Per la fase, invece, occorre analizzare in dettaglio l’andamento temporale, oppure ricorrere al diagramma XY:
Scalando opportunamente il grafico si ottiene una circonferenza, a conferma dello sfasamento di 90° dell'impedenza del condensatore.
Per completezza si riporta anche la tensione sul condensatore:
In conclusione possiamo dire che, con questo articolo di approfondimento, vi abbiamo mostrato un modo alternativo per simulare i circuiti elettrici che, in realtà, è utile per qualsiasi sistema dinamico, ed abbiamo effettuato una simulazione i cui risultati sono in accordo con la teoria.
Resto a vostra disposizione nei commenti per eventuali domande.





Ciao Gianluca, devo dire che i tuoi articoli mi piacciono molto, e mi interessano davvero tanto.
Certamente a breve sarò finalmente costretto ad usare Simulink, per cui credo che quando sarà necessario per prima cosa testerò i tuoi esercizi 🙂
Grazie. Mi fa piacere poter essere di aiuto. Spero che anche i prossimi articoli possano essere di interesse. Per ora in bocca al lupo con i tuoi studi. Se dovessi avere dubbi o difficoltà contattami pure.