
Quella presentata in questo articolo sembrerebbe un'operazione banale ed estremamente immediata, ma in realtà non è così. Trovare il centro perfetto dei tondini di legno e, in generale di un cerchio, non è proprio un'operazione così semplice e immediata. Tale procedura risulta molto importante, specialmente quando si lavora con il tornio. L'articolo propone diversi metodi, molti dei quali fattibili senza alcuna spesa aggiuntiva di realizzazione. Scegliamo quello più confacente ai nostri gusti e alle nostre esigenze.
Introduzione
Sono tantissime le occasioni nelle quali serve trovare il centro esatto di un cerchio o, nel nostro caso più specifico, quello di un tondino di legno o di altro materiale. Può servire, ad esempio, per piazzare e posizionare correttamente il pezzo da lavorare in un tornio. Può essere utile, altresì, per la realizzazione di ruote dentate, ingranaggi o altre parti in movimento, per le quali la rotazione degli stessi deve avvenire esattamente sull'asse centrale, al fine di non causare alcun tipo di oscillazione. Passiamo, di seguito, un'ampia rassegna dei metodi e delle tecniche che consentono di trovare il centro perfetto di una superficie circolare, non necessariamente di legno ma anche di altro materiale come, ad esempio, il marmo, il ferro, il cartone e così via.
Primo metodo: appoggio e rotazione
Iniziamo con il primo metodo, a mio avviso il più preciso e semplice da eseguire, e per il quale non è necessaria alcuna spesa di materiale aggiuntivo. Gli accessori occorrenti sono i seguenti:
- un blocchetto di legno grande o di altro materiale;
- un blocchetto di legno piccolo o di altro materiale;
- una matita ben temperata.
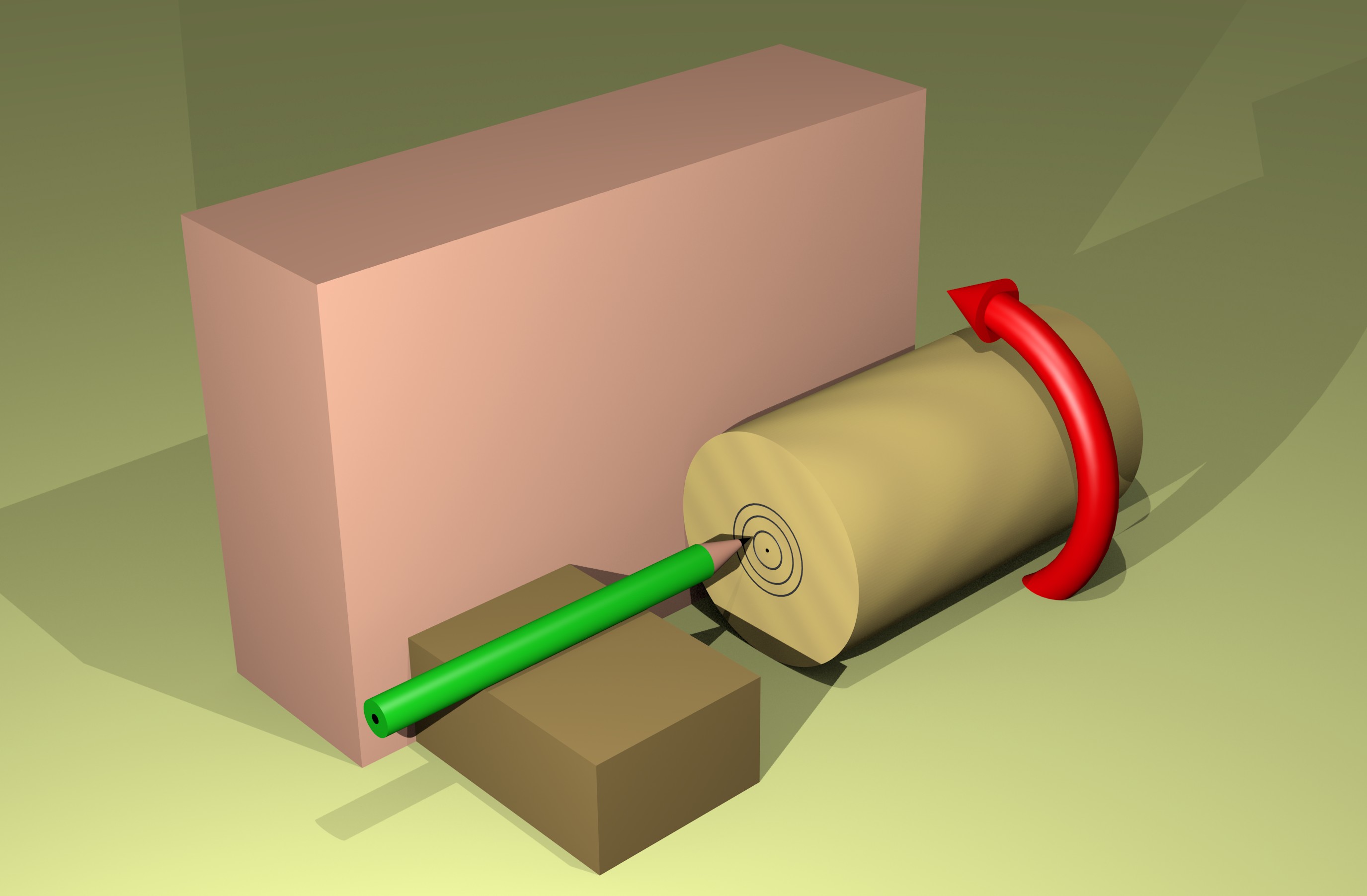
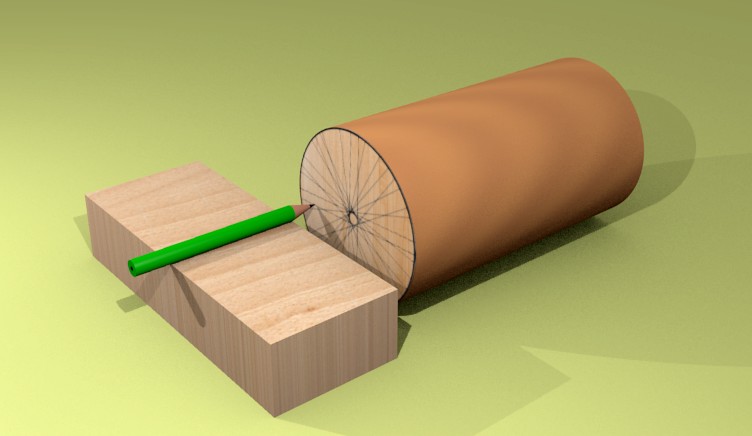
Si tratta di far ruotare il pezzo circolare contro un ostacolo assolutamente fermo e, nel contempo, lasciare che una matita tracci un leggero segno circolare sulla base del cilindro. La Figura 1 rende un pò meglio l'idea di principio. La dimensione dei blocchetti deve essere scelta in dipendenza da quella del cilindro.
La procedura da seguire è la seguente:
- si piazzi il tondino di legno vicino l'ostacolo grande;
- si piazzi una matita sopra un piccolo blocchetto, alto quanto circa la metà del tondino;
- si inizi a girare il tondino verso il blocchetto grande, nella direzione indicata dalla grossa freccia rossa;
- tenendo estremamente ferma la matita, si tracci una leggera circonferenza sulla base del tondino, durante la sua rotazione manuale;
- si consiglia di disegnare tre o quattro cerchi concentrici, via via sempre più piccoli.
Nell'utilizzare tale metodo è indispensabile che l'ostacolo verso cui ruota il tondino sia estremamente stabile e che, soprattutto, la matita non deve assolutamente basculare. Il blocchetto grande, allo scopo, può anche essere pesante, di ferro o di marmo. La Figura 2 mostra un tondino di legno su cui è stato ricavato il centro con tale metodo.
Non appena i due centri (uno per lato) sono stati ricavati, si può usare il pezzo di legno al tornio, per gli utilizzi più disparati. Sovente è consigliabile punzonare leggermente il centro, per evitare lo scivolamento della punta e della contropunta dell'attrezzo.
Secondo metodo: la squadretta a 45°
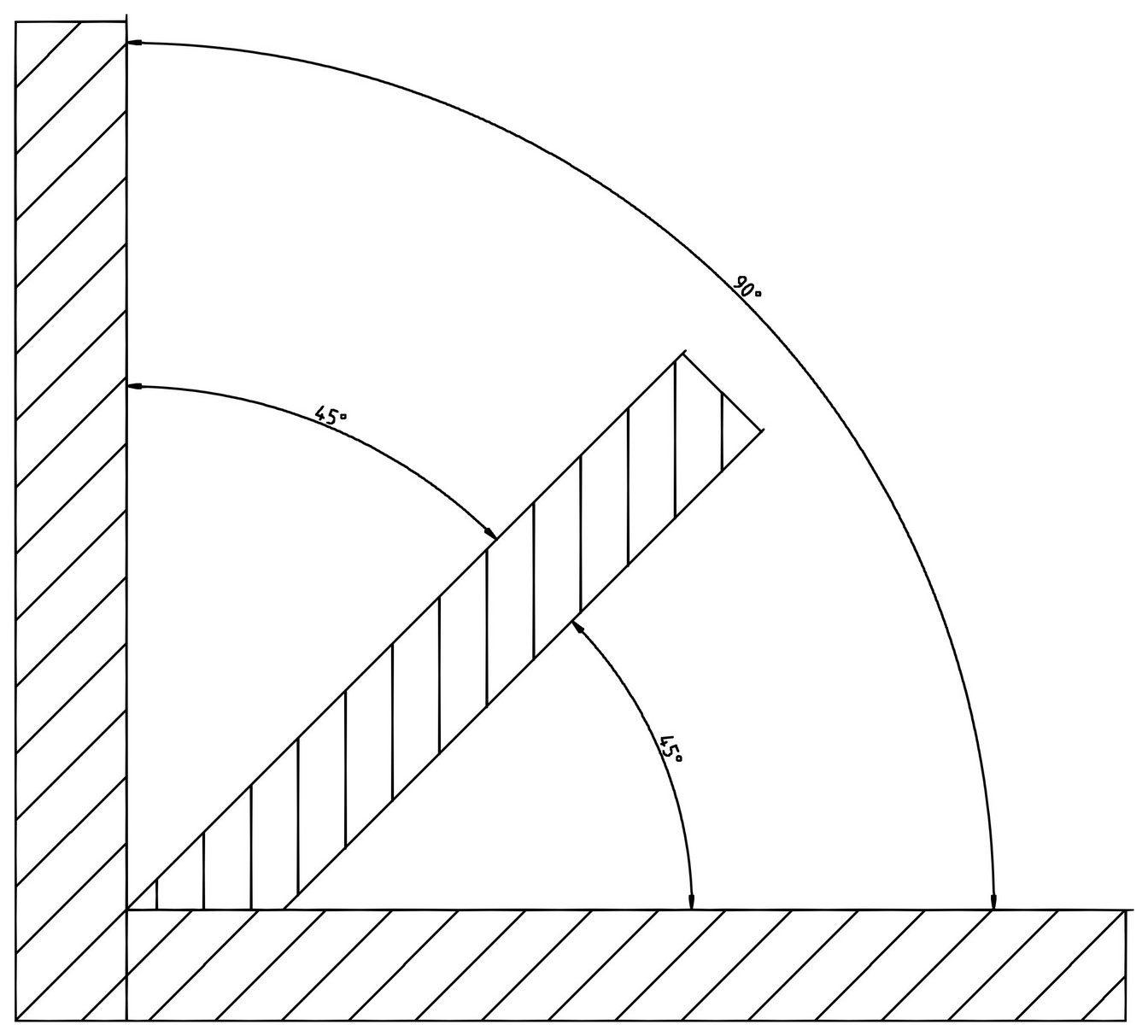
Il prossimo metodo è estremamente efficace, a patto che le varie fasi di lavorazione e, soprattutto, le operazioni di misura, siano condotte con la massima precisione possibile. Si tratta di costruire e di realizzare una semplice squadretta a 90°, con un registro a 45°, come mostrato in Figura 3.
In Figura 4 sono disponibili le quote per la sua realizzazione. Nella costruzione dell'attrezzo non è tanto importante la dimensione dell'oggetto stesso quanto l'esatta inclinazione del registro centrale, che deve essere perfettamente posizionato a 45° dai due assi principali. Quest'ultimo può anche essere realizzato di plexiglass trasparente.
L'utilizzo dell'attrezzo è molto semplice e, se la squadra è stata ben realizzata, può consentire di rintracciare il centro del cerchio in pochissimi istanti. Occorre, allo scopo, posizionare il tondino, di cui si deve trovare il centro proprio, a contatto delle due asticelle, come mostrato in Figura 5. Si tracci, quindi, un leggero segmento sul tondino con la matita, seguendo la linea del registro. Si prosegua con una seconda tracciatura, ruotando un po' il cilindro di circa 90°, in modo da ricavare una sorta di croce. L'intersezione dei due segmenti restituisce il centro matematico della faccia circolare. In pratica ciò che abbiamo realizzato serve a trovare il diametro della faccia di base del pezzo da lavorare.
Per agevolare la precisione della costruzione, si può realizzare la squadretta a 45° avvalendosi, magari, di un tondino di legno già tracciato con il primo metodo proposto e confrontando il punto centrale durante la realizzazione.
Terzo metodo: il foglietto piegato
Questo è un metodo a costo zero ed estremamente efficace. Si tratta di realizzare un cerchio di carta equivalente alla superficie del cerchio di cui si vuole trovarne il centro, come mostrato in Figura 6.
Quindi, con la massima precisione possibile, si pieghi il foglio a metà, prima per un diametro e poi per quello posto a 90°, come mostrato in Figura 7. Durante la piega, le due semicirconferenze opposte dovrebbero combaciare, segno inequivocabile di una perfetta divisione del foglio in due parti uguali. Le pieghe hanno il compito di segnare, appunto, i due diametri. Non occorre tracciare nulla sul cerchio di carta, in quanto le pieghe sono più che sufficienti per indicare i rispettivi diametri. Il punto in cui si intersecano i due segmenti costituisce, naturalmente, il centro del cerchio.
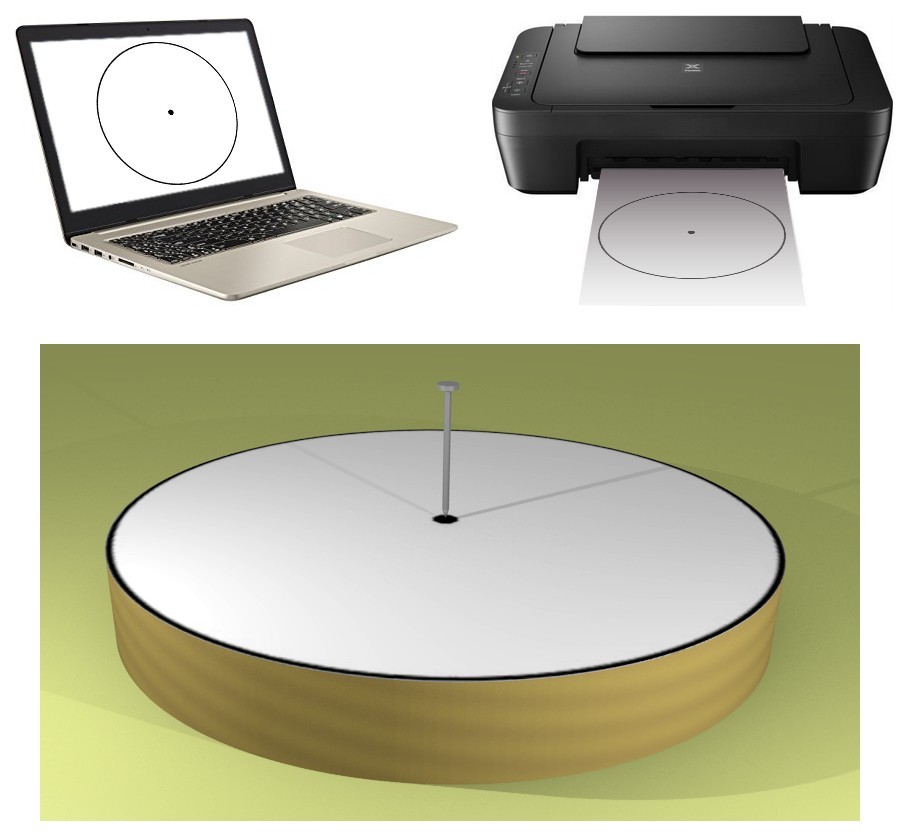
A questo punto è sufficiente praticare un minuscolo forellino con un piccolissimo chiodino, in corrispondenza esatta del centro. Quindi, si può adagiare il foglio di carta sul tondino di legno, facendo corrispondere le due circonferenze, come mostrato in Figura 8. Un minuscolo segno della matita indicherà il centro esatto del cerchio.
Quarto metodo: il cerchio inscritto in un quadrato
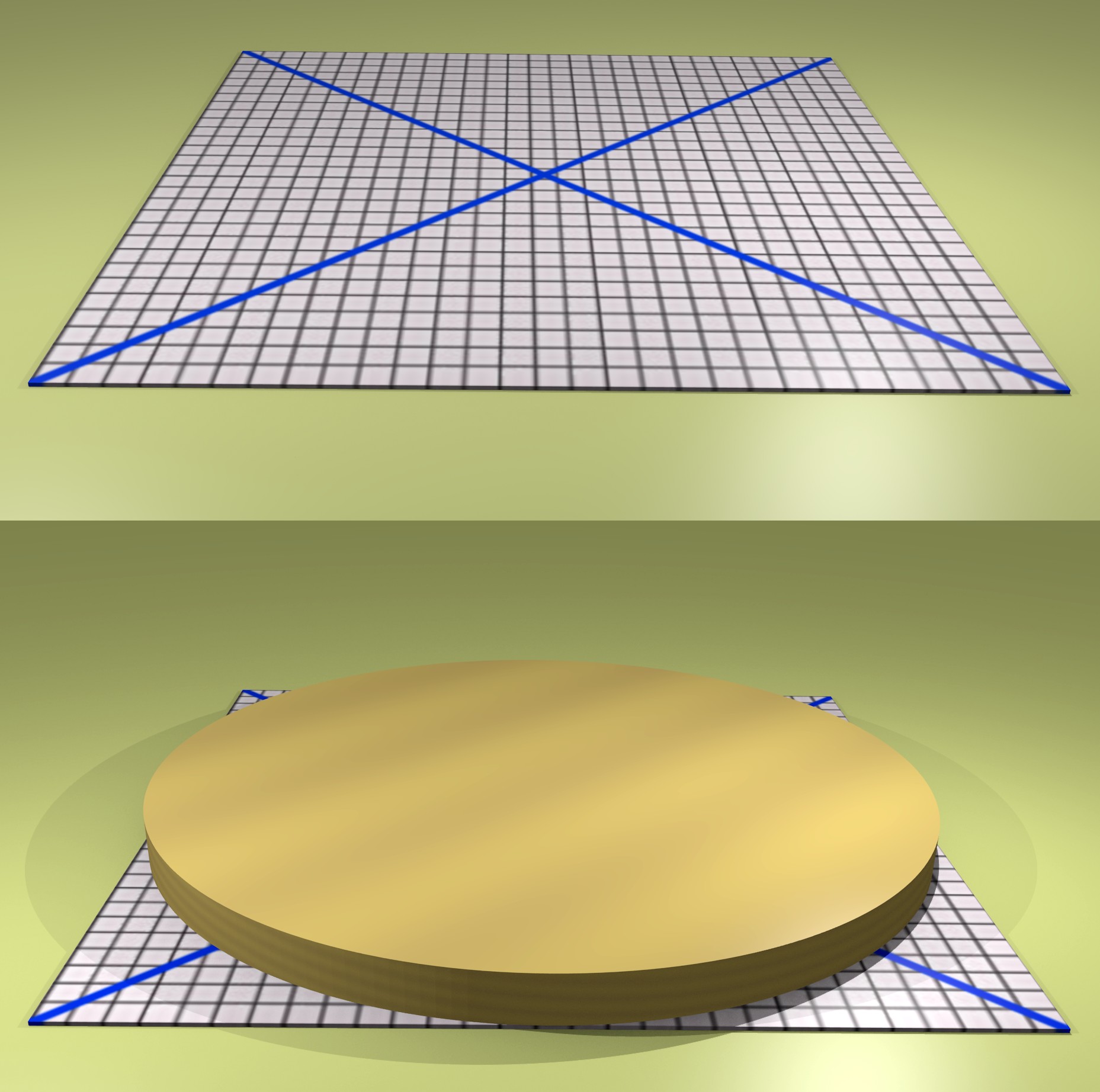
Per questa tecnica si deve procurare un foglio di carta a quadretti in cui il lato misuri quanto il diametro del cerchio di cui si vuol trovare il centro (vedi Figura 9). I due segmenti tracciati da spigolo a spigolo si incontrano perfettamente nel centro del quadrato e, di conseguenza, nel centro del cerchio. Per agevolare le operazioni di misura, si può posizionare il foglio di carta sopra il cilindro di legno, anziché sotto. Si utilizzi, dunque, tale punto per segnare, con una matita, il centro del cerchio.
Quinto metodo: intersezione dei diametri con il compasso
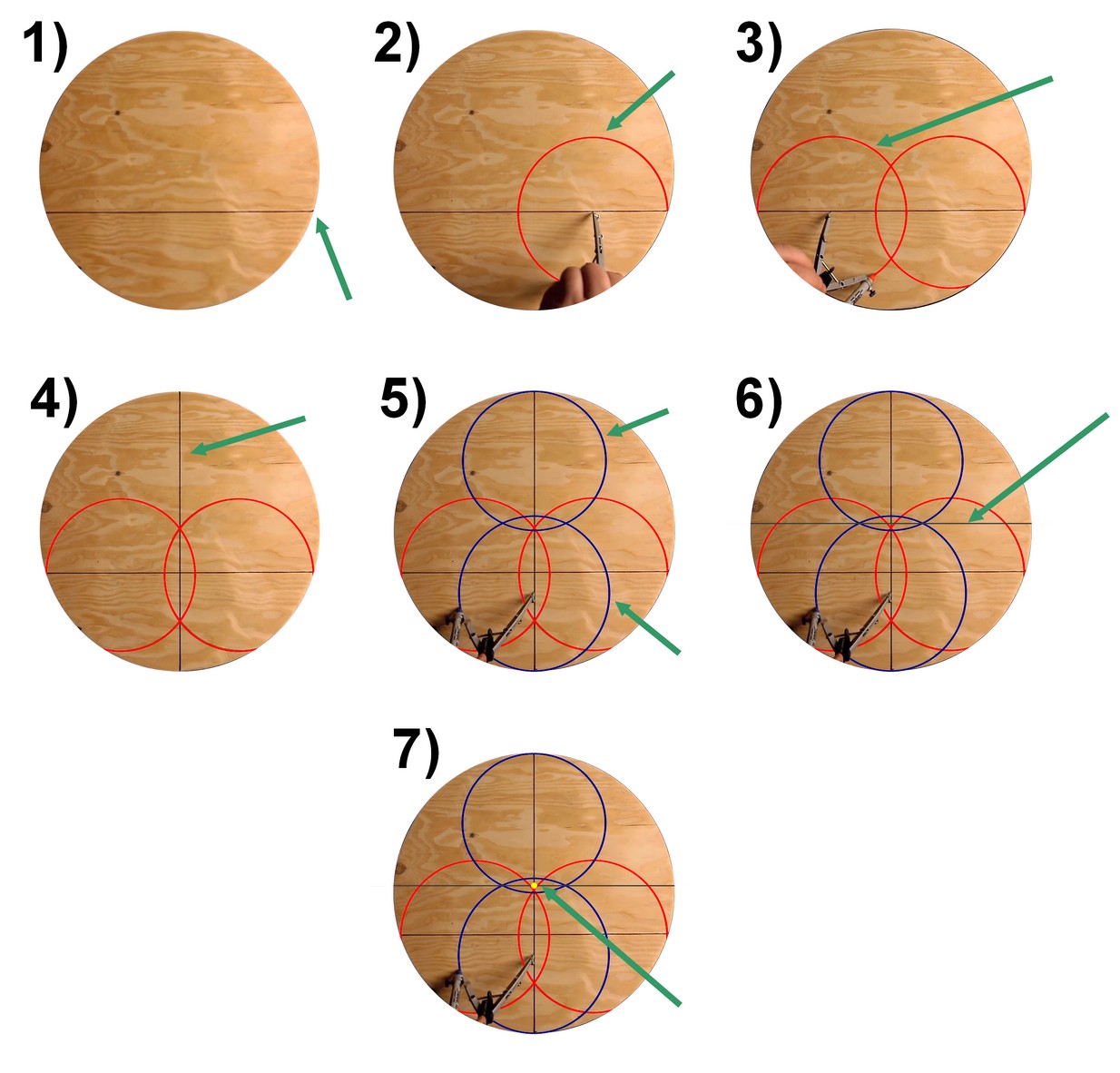
Il quinto metodo prevede l'uso del compasso e di una riga ed è adatto per la ricerca del centro anche in un cerchio particolarmente grande, diciamo con un diametro maggiore di 10 cm. La procedura è molto semplice e prevede il tracciamento di alcuni cerchi "di servizio", come descritto di seguito, seguendo le varie fasi di cui alla Figura 10:
- si tracci una corda arbitraria;
- si tracci un cerchio (di colore rosso) con centro sulla corda e raggio arbitrario che tocchi la circonferenza;
- con la stessa precedente apertura del compasso si tracci un altro cerchio (di colore rosso) sul lato opposto della corda;
- si congiungano le due intersezioni dei cerchi rossi tramite un segmento verticale. Abbiamo tracciato il primo diametro del cerchio;
- allo stesso modo, si traccino due cerchi uguali e opposti sul precedente diametro (di colore blu);
- con un segmento orizzontale si congiungano, adesso, le due intersezioni dei cerchi blu. Abbiamo tracciato il secondo diametro;
- l'intersezione dei due diametri costituisce, ovviamente, il centro del cerchio.
Sesto metodo: squadra a 90° e due corde
Ecco un altro metodo molto semplice e alla portata di tutti. Occorre utilizzare solamente una squadra a 90°. Esso si basa sulla regola che un triangolo inscritto in una circonferenza con un lato coincidente col diametro è sempre un triangolo rettangolo. Guardando la Figura 11 esaminiamo i passi operativi:
- si posizioni il vertice della squadra sulla circonferenza del cerchio e si traccino due corde (nella illustrazione di colore rosso);
- si rimuova la squadra e si congiungano tra loro le parti finali delle due corde. Abbiamo disegnato il primo diametro del cerchio. Si tratta dell'ipotenusa del triangolo rettangolo rosso;
- come per il punto 1, si ruoti di circa 90° la squadra, si posizioni il suo vertice sulla circonferenza e si traccino altre due corde (stavolta di colore verde);
- si rimuova la squadra e si congiungano tra loro le parti finali delle due corde. Abbiamo disegnato il secondo diametro del cerchio. Anche in questo caso si tratta dell'ipotenusa del triangolo rettangolo verde;
- l'intersezione dei due diametri costituisce, ovviamente, il centro esatto del cerchio.
Questo metodo è utilizzabile anche per grandi figure, purché sia assicurata la presenza dell'angolo retto tra le due corde.
Settimo metodo: la stampante
Grazie all'aiuto di una stampante (a getto d'inchiostro oppure laser) si può facilmente trovare il centro di un cerchio. Occorre usare un programma di grafica o, meglio ancora, di un C.A.D (Computer Aided Design). Si deve disegnare, in scala 1:1, una circonferenza perfettamente uguale a quella della forma in questione. Altresì, occorre tracciare anche il centro, con un piccolo punto nero. Con un software adatto tale operazione è un gioco da ragazzi. Si stampi, quindi, il lavoro su foglio di carta e si ritagli alla perfezione il cerchio, magari servendosi di un cutter. Si sovrapponga, quindi, il foglio sul pezzo di legno o di altro materiale e, attraverso un piccolo chiodo e la leggera pressione di un martellino, si segni il centro. La Figura 12 illustra molto chiaramente tale operazione. Più piccolo risulterà il disegno del punto centrale e migliore sarà la precisione raggiunta. Diciamo che un suo diametro di un millimetro può andare senz'altro bene.
Ottavo metodo: il marcatore con una lama
Si tratta di un utile attrezzo di precisione, da costruire con alcuni spezzoni di legno e una lama di un cutter. Il prototipo finale può essere osservato in Figura 13.
Il procedimento della realizzazione è estremamente semplice. La lama è posta esattamente a 45° sulla base, dalla quale ne sporge solo una minima porzione, diciamo circa mezzo millimetro. Anche l'utilizzo risulta essere immediato. E' sufficiente posizionare il pezzo circolare sulla base, in modo che esso aderisca perfettamente alle due pareti laterali. Un leggero colpo di martello permetterà l'incisione di un sottile solco sulla faccia opposta del cilindro. Occorreranno, naturalmente, due solchi la cui intersezione costituirà il centro esatto del cerchio.
Nono metodo: tante tracce sulla base
Anche questo metodo è molto ingegnoso quanto semplice e non occorre alcun materiale, se non una matita e un piccolo spessore di legno. Occorre posizionare la matita sopra lo spessore, a un'altezza poco inferiore del centro del cerchio (a occhio essa si riesce a determinarla piuttosto facilmente). Quindi si deve passare il cilindro di legno accanto la matita, trascinandolo, per effettuare una prima traccia. Se lo si desidera, si può anche trascinare la matita e lasciare fermo il cilindro di legno. Il risultato finale sarà equivalente. Si ruoti, quindi, il cilindro sul suo asse e si effettui una seconda traccia. Si ripeta, infine, la procedura per una decina di volte, ruotando sempre il cilindro su se stesso. I segmenti tracciati vanno a disegnare un piccolo cerchio centrale indicante il punto cercato. La Figura 14 mostra la tecnica utilizzata. Quanto più le tracce si avvicinano al centro del cerchio, tanto più preciso sarà il risultato finale.
>>>Leggi anche: Costruiamo un portabottiglie equilibrista in legno
Conclusioni
Come abbiamo visto nell'articolo, siamo riusciti a trovare e ad esaminare una buona quantità di metodi per la ricerca del centro di un cerchio. Alcuni di essi estremamente pratici, semplici e validi, altri più geometrici. La problematica esaminata nell'articolo costituisce una delle più importanti nel settore del fai da te e dell'hobbistica. A volte, le soluzioni a problemi relativamente complicati sono estremamente semplici, anche se non si trova immediatamente, e a colpo d'occhio, la corretta modalità operativa. Sicuramente esistono altri metodi, alcuni semplicistici e altri più scientifici e matematici. Esortiamo i lettori a contribuire con i propri commenti e le proprie idee. Buon lavoro a tutti!














I centri e i comuni metodi per trovarli sono frequenti nelle applicazioni hobbistiche che richiedono una certa dimestichezza nel calcolo e nel disegno tecnico. Altresì il concetto di centro riveste una importanza basilare nello studio cinematico dei sistemi, dove dallo studio del centro di istantanea rotazione possiamo dedurre la natura dell’atto di moto di un corpo o di un componente.
L’articolo descrive molto bene l’applicazione della geometria nel campo dell’hobbistica e mostra come non bisogna avere chissà che grande attrezzatura per essere precisi ma sicuramente grande inventiva. Chi conosce bene la geometria si può divertire veramente tanto..
Molto bello,
riguardo al primo metodo suggerirei di tracciare delle scanalature nel legno , nella direzione
dell’ asse della matita, utilizzando una squadretta da falegname ed abbastanza vicine l’une all’altra in modo da bloccarla ed impedirne il movimento durante la tracciatura dei cerchi.
Lo stesso anche per il metodo in fig. 14
Saluti
Articolo bello, completo e con tante illustrazioni. Non pensavo potessero esistere tanti metodi per la tracciatura di un centro di un cerchio. Lavorando con il CAD tutto si riduce ad utilizzare uno Snap applicato all’oggetto cerchio e il gioco è fatto.
Bene anche tutti i riferimenti alla geometria.
Chissà quale avrà utilizzato per primo l’inventore della ruota!
Comunque gli articoli di Giovanni Di Maria sono sempre una garanzia!
Il terzo metodo, quello del foglietto piegato, mi sembra il più semplice, quindi immediato, e anche economico. Poi certo molto dipende dall’oggetto e dalle dimensioni ma oggi ho fatto un sano tutto nei ricordi di geometria. Grazie all’autore!
Molto interessante. Spesso mi ritrovo, nei miei lavoretti obbistici, di trovare il centro di un tondino o di un pezzo circolare. Per quanto riguarda il tondino, io usavo il metodo di metterlo nel mandrino del trapano e segnare con la matita il centro, ma il mio trapano ha il il mandrino un po’ eccentrico e quindi non mi da’ il centro perfetto. La prossima volta che ne avrò bisogno userò uno di questi metodi.
interessante. aggiungerei un metodo un pò “empirico” con l’uso di un banale compasso:
si allarga il compasso fin quasi ad avere il raggio preciso del pezzo su cui “puntare” il centro, poi pian piano si posiziona sul probabile centro la punta del compasso e si prova a far girare per vedere se si “copre” bene tutta la circonferenza.
Articolo veramente originale, complimenti. In effetti può essere una problematica con la quale ci si può scontrare e che di primo acchitto magari lascia perplessi.
Esiste un altro metodo per trovare il centro di un cerchio e che richiede solamente un compasso (o spago con una punta legata da un lato e una matita dall’altro) e una riga.
1) con la riga si traccia una corda a caso A.
2) con il compasso si punta uno dei due estremi della corda A e si tracciano due archetti uno interno e uno esterno al cerchio.
3) si ripete l’operazione ma puntando il compasso sull’altro estremo della corda A in modo da intersecare gli archetti precedenti.
4) Con la riga si congiungono le intersezioni degli archetti stessi.
Si ripetono i punti da 1 a 4 tracciando un’altra corda a caso B che però non intersechi la precedente.
Quando si congiungeranno le intersezioni dei nuovi archetti, si fa in modo che la retta tracciata intersechi quella tracciata al punto 4 o un suo eventuale prolungamento.
L’intersezione finale sarà il centro del cerchio.
Un problema pratico, solo in apparenza semplice: come fare un foro al centro del coperchio di un barattolo? Questo articolo dovrebbe essere incluso nei programmi di istruzione elementare!
Molte grazie per aver condiviso le basi di geometria e con strumenti che chiunque potrebbe avere sottomano.