
Continua il corso dedicato agli Aeromobili a Pilotaggio Remoto (APR). Nell'articolo precedente abbiamo analizzato cos'è un sistema di riconoscimento e la loro importanza nei droni, introducendo l'idea di visione artificiale ed object detection, focalizzando l'attenzione sui simulatori di scenari ed i sistemi di riferimento. Nella puntata di oggi descriveremo il modello matematico di un multi-rotore, in particolare quello di un esacottero, utilizzando due differenti approcci: Eulero-Lagrange e Newton-Eulero. Ricavate le equazioni del moto ne esprimeremo l'equivalente rappresentazione nella forma dello spazio di stato, fondamentale per la simulazione del velivolo nello scenario virtuale (e non solo) nonché per la progettazione del controllo di volo (argomento del prossimo articolo). Il tutto verrà affrontato senza scendere in tediosi dettagli tecnici matematici, fornendo al contempo le basi necessarie per successivi approfondimenti.
Nozioni preliminari
Per descrivere il modello matematico di un multi-rotore è necessario riprendere quanto introdotto, nella seconda puntata di questo mini-corso, in merito ai sistemi di riferimento. Difatti, è possibile utilizzare il sistema di riferimento verticale-locale e quello assi corpo [In letteratura è indicato con il pedice ABC, acronimo di Aircraft Body Center] per la modellazione del sistema: il primo definisce la posizione lineare assoluta (x, y e z), il secondo l'orientamento (ψ, φ e θ) del velivolo. In Figura 1 è evidenziata la relazione tra i due sistemi di riferimento.
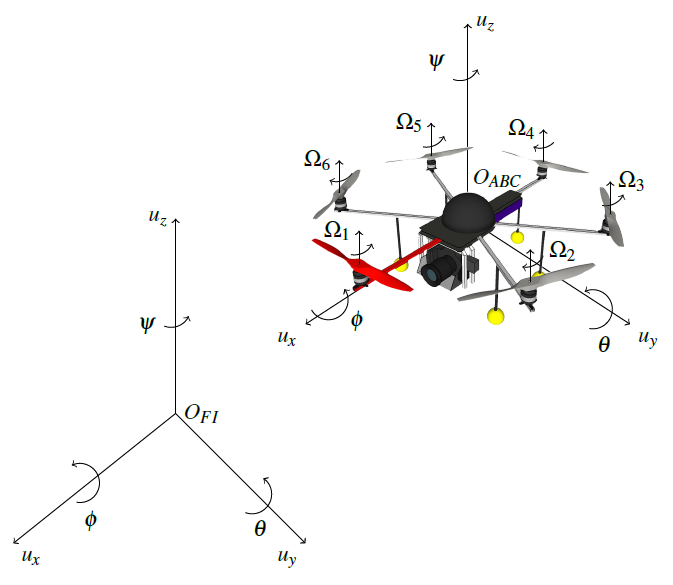
Figura 1: Drone nel sistema di riferimento assi corpo (ABC, destra) e in quello inerziale (FI, sinistra).
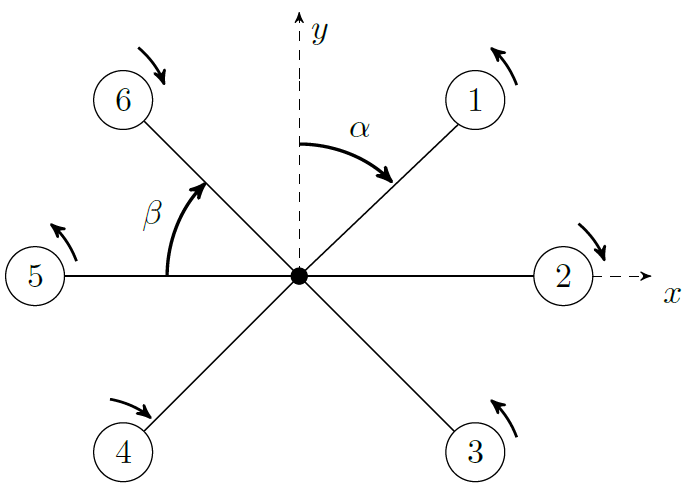
L'altitudine e la posizione dell'aeromobile possono essere controllate, portandole al valore desiderato, variando la velocità dei sei motori di cui è equipaggiato il drone. Le forze ed i momenti che si gerano modificano così le prestazioni dell'APR: la spinta è una diretta conseguenza dell'aumento di velocità delle pale, il momento di beccheggio e quello di rollio, invece, sono ottenuti da un cambiamento della spinta fornita dai sei motori, dalla gravità, dagli effetti giroscopici e dal momento di imbardata (argomenti chiariti nel seguito dell'articolo).
Il momento di imbardata, la cui origine è da individuare nella differente velocità dei sei propulsori, può essere cancellato modificando il verso di rotazione delle eliche: tre si muoveranno in senso orario e tre in senso antiorario. Le eliche si dividono, quindi, in due gruppi diametralmente opposti, facilmente individuabili grazie allo stesso verso di rotazione. Al contrario, gli effetti giroscopici costituiscono una caratteristica dei droni commerciali di piccole dimensioni, noti anche come MAV (Micro Aerial Vehicle), di cui l'esempio più noto è l'AR.Drone. Si tratta di effetti difficilmente eliminabili ma di facile compensazione attraverso l'utilizzo di tecniche ben note in letteratura.
Volendo essere quanto più precisi possibili, incrementando o decrementando la velocità di rotazione delle eliche si determina il cambiamento dell'altitudine in posizione e velocità, mentre variando la velocità delle due eliche (Ω1 e Ω6 o Ω3 e Ω4) si causa una rotazione del velivolo intorno all'asse y il quale descrive un angolo di beccheggio indicato con θ. In modo del tutto simile variando la velocità di rotazione delle tre eliche (Ω1, Ω2 e Ω3 o Ω4, Ω5 e Ω6) causeremo una rotazione dell'aeromobile intorno all'asse x descrivendo un angolo di rollio indicato con φ. Infine, il vettore somma dei momenti di reazione ottenuto dalla rotazione di Ω1, Ω3 e Ω5 ed i momenti di reazione prodotti dalla rotazione di Ω2, Ω4 e Ω6 causeranno una rotazione dell'esacottero intorno all'asse z descrivendo un angolo di imbardata indicato con ψ (per maggiori dettagli si veda quanto esposto nella prima puntata, in merito al funzionamento di un velivolo multi-rotore).
Per quanto concerne lo spazio del moto, quello di un APR è diviso in due parti: i movimenti del baricentro e quelli intorno al baricentro. Sei DOFs (Degree of Freedom) sono richiesti per descrivere il suo andamento nel tempo. Tre esprimono i movimenti del baricentro e tre quelli angolari, ovvero, i tre moti traslazionali (x, y e z) e tre rotazionali (ψ, φ e θ).
Come sopraccitato, il controllo dei sei DOFs è ottenuto variando le velocità di rotazione dei sei motori. Quindi, il sistema nel suo complesso è formato da sei variabili in ingresso e sei in uscita e, come vedremo più avanti quando giungeremo alle equazioni del moto, si tratta di un sistema fortemente non lineare.
In definitiva, un multi-rotore è un sistema meccanico complesso, una raccolta di effetti fisici di diverso dominio. Al fine di sintetizzare il modello matematico si è assunto che:
- la struttura dell'aeromobile sia rigida e simmetrica;
- il centro di gravità e l'origine del corpo coincidono;
- le eliche sono indeformabili;
- la spinta è proporzionale al quadrato della velocità dei rotori.
Modellazione con Eulero-Lagrange
In questa sezione sono modellate le dinamiche di rotazione utilizzando il formalismo di Eulero-Lagrange. Tale metodologia (già descritta ed utilizzata in un precedente articolo) di analisi utilizza il baricentro energetico per ottenere l'insieme di equazioni che descrivono il comportamento del sistema.
Cinematica
Per un punto P (xp, yp e zp) dello spazio, espresso nel sistema di riferimento verticale-locale, si può scrivere:
Le relative velocità, ottenute derivando l'equazioni precedenti, consentono così di calcolare la radice quadrata dell'ampiezza delle velocità per un dato punto P:
Energia
Partendo dalla (eq. 2), assumendo che la matrice d'inerzia I sia diagonale, è possibile estrarre l'equazione cinematica dell'energia (eq. 4).
Utilizzando la nota formula che descrive l'energia potenziale V, è possibile esprimere la (eq. 4) nel sistema di riferimento verticale-locale come:
Noti i legami dell'energia cinetica (eq. 4) e di quella potenziale (eq. 5) è possibile, finalmente, descrivere l'equazioni del moto (paragrafo successivo).
Equazioni del moto
Utilizzando la Lagrangina L è possibile derivare le formule che descrivono il moto del velivolo (eq. 7) partendo dall'espressione generale:
dove la derivata di qi è Γi indicano rispettivamente le coordinate del sistema e le forze generalizzate. Da qui, è possibile scrivere:
Dall'altra parte, le coppie non conservative agiscono sul multi-rotore in primo luogo con l'azione di una spinta differente per ogni coppia (Figura 2):
Oltre agli effetti giroscopici che pongono in rotazione le eliche, e che possono essere tenuti in conto come:
Il modello matematico derivato
Il modello matematico del multi-rotore derivato, in sintesi, descrive le rotazioni dell'angolo di rollio (φ), imbardata (ψ) e beccheggio (θ), contiene tre termini che tengono conto degli effetti giroscopici risultanti dalla rotazione del corpo rigido (τx, τy e τz) e di quelli derivanti dai due gruppi di eliche (τx' e τu'), ed infine dell'azione degli attuatori:
La dinamica dei rotori
I rotori che equipaggiano il velivolo sono costituiti dai sensori AC, di cui bene note sono le equazioni che ne descrivono la dinamica:
Per chi non ne conoscesse la struttura, ricordo di leggere le precedenti lezioni del corso e quanto presente in un precedente articolo.
I motori presentano un piccolo valore di induttanza, per tale ragione la dinamica del secondo ordine può essere approssimata come:
A questo punto, introducendo i modelli delle eliche e della scatola di trasmissione, l'equazione (eq. 12) può essere riformulata come:
Da qui, è possibile linearizzare l'equazione (eq. 13) intorno ad un generico punto di lavoro, la derivata di ω0, e scriverla nella forma:
con
Modellazione con il formalismo di Newton-Eulero
Il modello ottenuto attraverso il formalismo di Newton-Eulero è sviluppato per passi successivi. La versione descritta in questo articolo include le forze che agiscono sui mozzi H, i momenti di rollio Rm ed i coefficienti variabili aerodinamici J. Quest'ultimi rendono il modello più realistico particolareggiandolo per il volo in ambienti outdoor. Il fine ultimo è quello di introdurre il modello impiegato per lo sviluppo del sistema di controllo progettato (argomento del prossimo appuntamento) utilizzando la tecnica Integral Backstepping, combinazione tra la classica PID (lineare) e quella Backstepping (non lineare).
La dinamica del corpo rigido, sottoposta all'azione delle sopraccitate forze esterne applicate al centro di massa ed espresse nel sistema di riferimento assi-corpo con il formalismo di Newton-Eulero, è descritta dalle equazioni di seguito:
Si ricorda l'utilizzo del sistema di riferimento verticale-locale e di quello assi-corpo, come mostrato in Figura 1, per descrivere il moto dell'aeromobile. Dunque, utilizzando la parametrizzazione degli angoli di Eulero, l'orientamento del velivolo nello spazio è dato dalla rotazione tra un sistema di riferimento e l'altro come descritto nel secondo episodio di questo mini-corso.
Quanto formulato altro non è che una generalizzazione del modello matematico che descrive il comportamento di un quadri-rotore, particolare tipologia di multi-rotore.
Forze e momenti aerodinamici
Le forze ed i momenti aerodinamici sono derivati utilizzando una combinazione teorica sulla quantità di moto delle pale del velivolo. Per una veloce lettura delle equazioni di seguito sono riportati i significati dei simboli utilizzati:
[...]
ATTENZIONE: quello che hai appena letto è solo un estratto, l'Articolo Tecnico completo è composto da ben 2350 parole ed è riservato agli ABBONATI. Con l'Abbonamento avrai anche accesso a tutti gli altri Articoli Tecnici che potrai leggere in formato PDF per un anno. ABBONATI ORA, è semplice e sicuro.


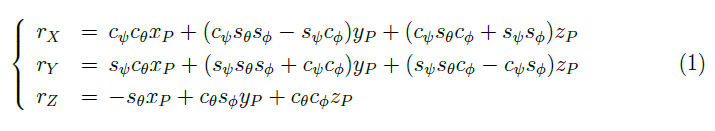

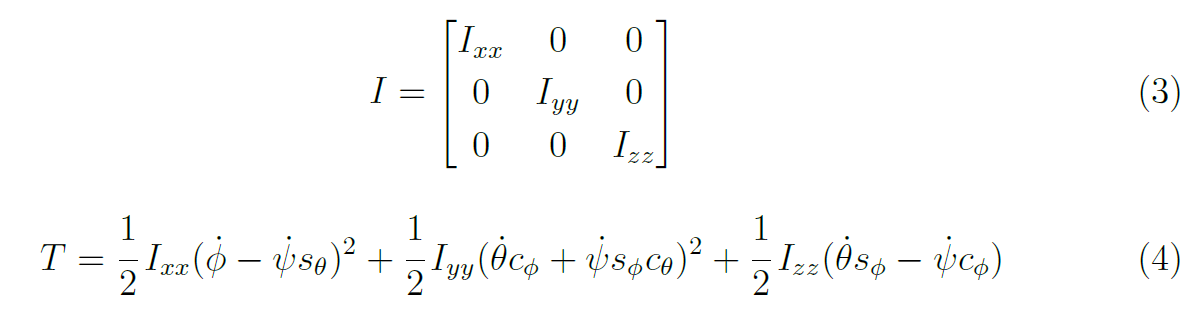
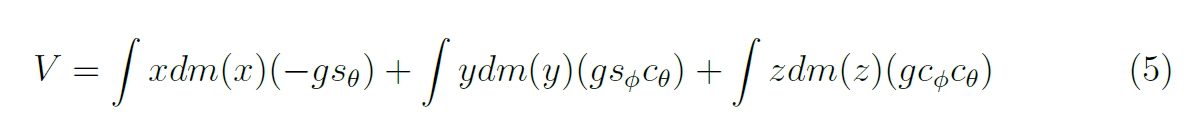
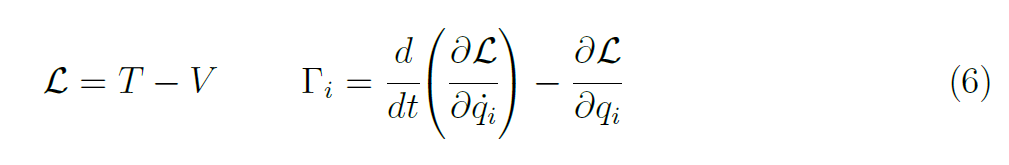
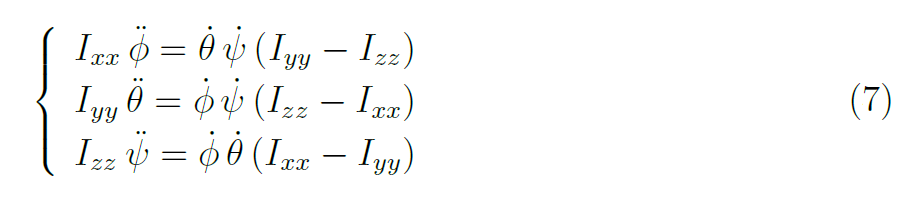
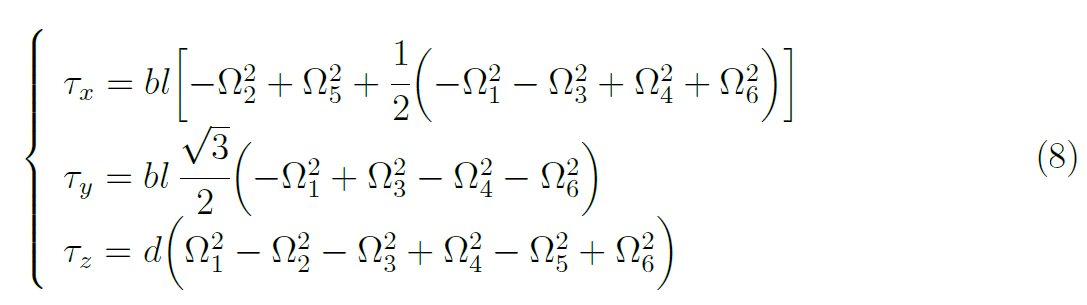

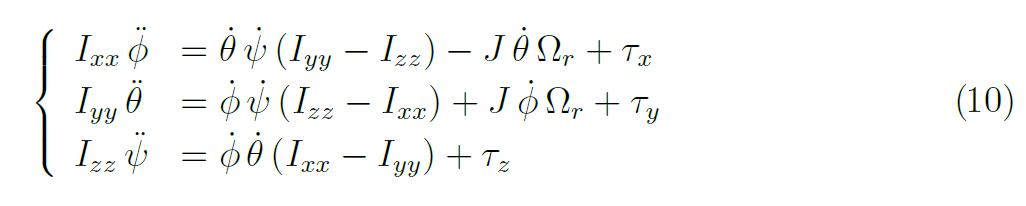
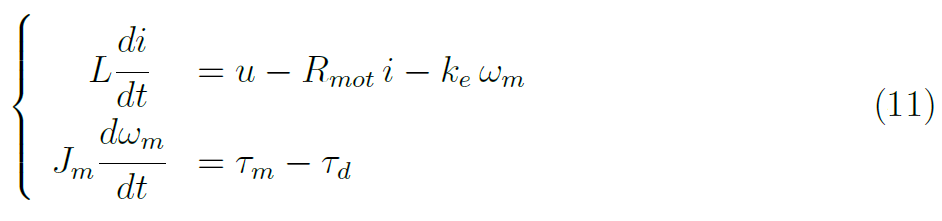
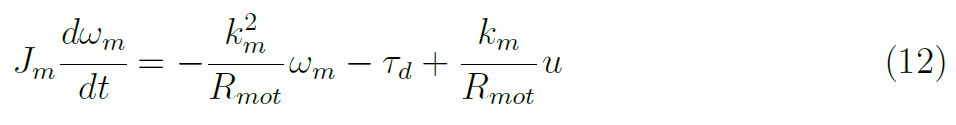


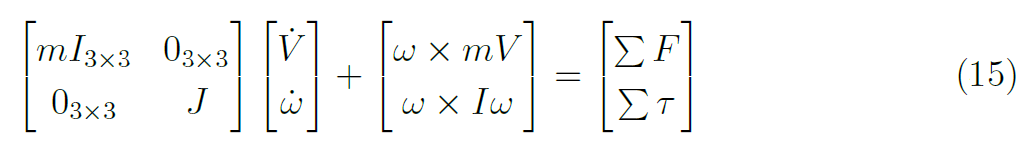





Bellissimo articolo, grazie!