Gli effetti degli elementi parassiti sulla misura dell’impedenza

L'impedenza è un parametro importante utilizzato per caratterizzare i circuiti elettronici, i componenti ed i materiali utilizzati per realizzare i componenti. Questo articolo si concentra sugli effetti degli elementi parassiti e di vari fattori che influenzano la misurazione dell’impedenza.

Introduzione - Impedenza

L'impedenza (Z) è generalmente definita come l'opposizione totale che un dispositivo o circuito impone al flusso di una corrente alternata ad una data frequenza, ed è definita come una quantità complessa rappresentata graficamente su un piano vettoriale. Il vettore dell’impedenza è costituito da una parte reale (resistenza R) ed una parte immaginaria (reattanza X) come mostrato nel diagramma polare di Figura 1 in cui l’impedenza è rappresentata da un vettore di modulo |Z| e fase θ.

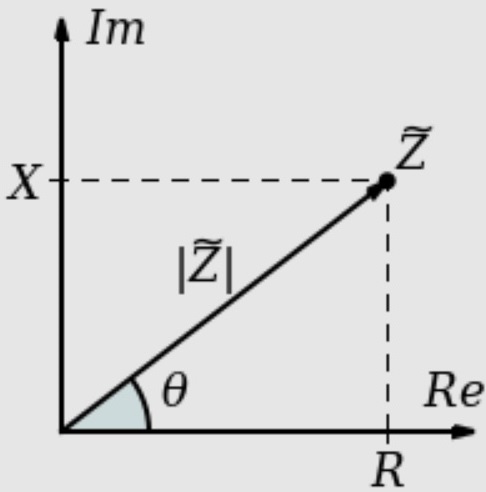
Figura 1: Impedenza su un piano vettoriale

L'impedenza può essere espressa utilizzando la forma a coordinate rettangolari R + jX, o nella forma polare come ampiezza (il modulo |Z|) e angolo di fase θ. La Figura 2 mostra la relazione matematica dell’impedenza in serie, parallelo e dell’ammettenza.

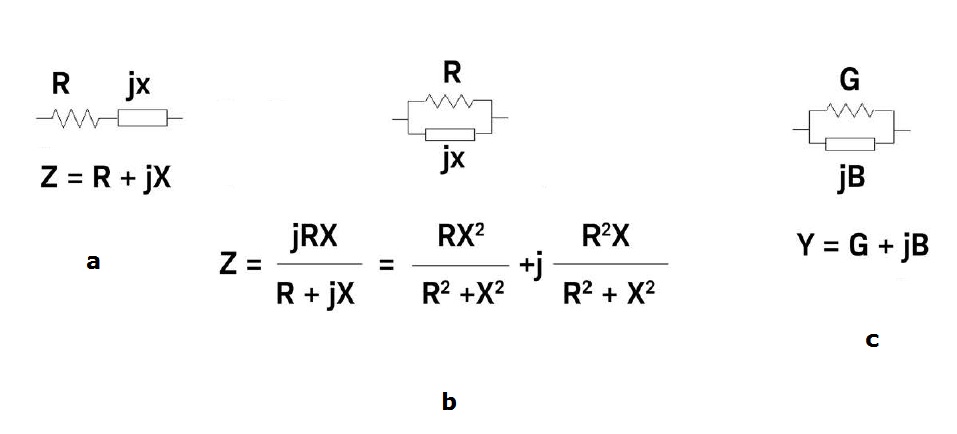
Figura 2: Schemi e calcolo dell’impedenza

La Figura 2.a mostra l’impedenza costituita da elementi in serie, la Figura 2.b da elementi in parallelo e la Figura 2.c rappresenta l’ammettenza, ovvero il reciproco dell'impedenza. In alcuni casi, utilizzare il reciproco dell'impedenza è matematicamente conveniente in quanto si semplificano molto i calcoli. In questo caso 1/Z = 1/(R + jX) = Y = G + jB, dove Y è l'ammettenza costituita dalla conduttanza G e dalla suscettanza B. L'unità di misura dell’impedenza è l'ohm (Ω) e dell’ammettenza è il siemens (S). L'impedenza è un parametro comunemente usato ed è particolarmente utile per rappresentare un collegamento in serie di resistenza e reattanza, in quanto può essere espressa semplicemente come somma di R e X. Per una connessione parallela di R e X, è meglio usare l'ammettenza il cui calcolo si riduce ad una somma, come mostrato in Figura 2.c. La reattanza assume due forme: induttiva (XL) e capacitiva (Xc). Per definizione, la reattanza di un induttore è XL = 2πfL, mentre la reattanza di un capacitore è Xc = 1/(2πfC), in cui f è la frequenza di interesse, L è l'induttanza e C è la capacità. Il termine 2πf può essere sostituito dalla frequenza angolare ω (si legge “omega”), quindi, XL = ωL e Xc =1/(ωC). La Figura 3 mostra il diagramma polare dell’impedenza di un induttore (Figura 3.a) e di un capacitore (Figura 3.b).

Figura 3: Diagramma polare dell’impedenza di un induttore (a) e di un capacitore (b)

Un parametro molto importante di un’impedenza è il fattore di qualità Q. Il fattore di qualità indica la misura della purezza di una reattanza, ossia quanto è prossima ad essere una pura reattanza, ovvero priva di resistenza, ed è definito come il rapporto tra l'energia immagazzinata in un componente e l'energia dissipata dal componente. Il fattore Q è adimensionale ed è espresso dal rapporto Q = X/R o B/G. Essendo X e R rispettivamente il seno(θ) e il coseno(θ) del vettore di modulo unitario |Z| e angolo θ, quindi, si può anche scrivere Q=tang θ.

Osservando i diagrammi polari di Figura 3, possiamo vedere che per l’induttore, Q =XL/R e per il capacitore, Q=-XC/R. Si deduce che più è basso il valore della resistenza dell’impedenza, maggiore sarà il valore di Q. Il fattore Q è comunemente applicato agli induttori; per i condensatori, il termine più spesso utilizzato per esprimere la purezza della reattanza capacitiva è il fattore di dissipazione (D), o il rapporto tra l’ESR e la reattanza capacitiva. Questa quantità è semplicemente il reciproco di Q, 1/Q è quindi la tangente dell'angolo complementare di θ, l'angolo δ mostrato nei diagrammi di Figura 3.

Misura dell'impedenza

Per rilevare il valore dell’impedenza, dobbiamo misurare almeno due valori perché l'impedenza è una quantità complessa. Molti moderni strumenti di misura dell'impedenza misurano le parti reali e immaginarie di un vettore di impedenza e poi le convertono nei parametri desiderati come |Z|, θ, |Y|, R, X, G, B, C e L. Per questo, è necessario solo collegare allo strumento il componente, il circuito o il materiale sconosciuto da testare. Il range della misurazione e la precisione per una varietà di parametri di impedenza sono determinati da quelli specificati per la misurazione dell'impedenza. Tuttavia, a volte lo strumento visualizza un risultato imprevisto (troppo alto o troppo basso). Una possibile causa di questo problema è una tecnica di misurazione errata o il naturale comportamento del dispositivo sconosciuto. Di seguito, ci concentreremo sui componenti passivi tradizionali descrivendone il comportamento naturale nel mondo reale rispetto al comportamento ideale.

Gli elementi parassiti dei componenti reali

Gli attributi principali delle componenti L, C e R sono generalmente rappresentati dai valori nominali di capacità, induttanza o resistenza in condizioni specificate o standardizzate. Tuttavia, tutti i componenti di un circuito non sono né puramente resistivi, né puramente reattivi. Coinvolgono entrambi questi elementi dell’impedenza. Ciò significa che tutti i dispositivi del mondo reale hanno elementi parassiti come induttanza indesiderata nei resistori, resistenza indesiderata nei condensatori, capacità indesiderata negli induttori, ecc. Materiali diversi e tecnologie di produzione producono quantità variabili di parassiti. In effetti, molti parassiti risiedono nei componenti, influenzando sia l'utilità di un componente che la precisione con cui è possibile determinarne il valore di resistenza, capacità o induttanza. Con la combinazione dell'elemento primario e dei parassiti del componente, un componente sarà come un circuito complesso rappresentato da un modello di circuito equivalente come mostrato nella Figura 4 in cui viene riportato lo schema di un induttore reale.

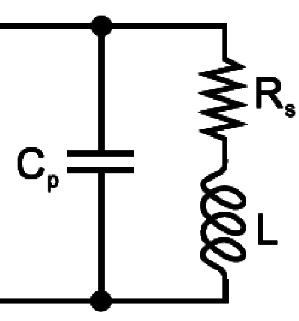
Figura 4: Circuito equivalente di un induttore reale

Nello schema di Figura 4, gli elementi parassiti di un induttore sono la resistenza Rs e il condensatore Cp rispettivamente in serie e in parallelo all’induttanza L. Poiché i parassiti influenzano le caratteristiche dei componenti, i valori dei parametri C, L, R, D, Q e altri parametri di un’impedenza intrinseca, variano a seconda delle condizioni operative dei componenti.

[...]

ATTENZIONE: quello che hai appena letto è solo un estratto, l'Articolo Tecnico completo è composto da ben 2065 parole ed è riservato agli ABBONATI. Con l'Abbonamento avrai anche accesso a tutti gli altri Articoli Tecnici che potrai leggere in formato PDF per un anno. ABBONATI ORA, è semplice e sicuro.