
Tutti noi utilizziamo quotidianamente dispositivi elettronici che contengono almeno un circuito a ponte. Molti tra noi hanno utilizzato, almeno in qualche occasione, le sue forme più comuni in fase di progetto. Pochi però possono affermare di conoscere in dettaglio tutte le diverse applicazioni di questo utilissimo schema circuitale, accuratamente descritte nelle pagine che seguono.
Il concetto di ponte in elettronica è ampiamente diffuso, generalmente con ponte si intende una configurazione circuitale composta da due rami in parallelo, costituenti quindi una maglia, connessi ad una sorgente di alimentazione. In questo articolo della Rubrica Firmware Reload vedremo alcune delle tipologie più comuni di circuiti a ponte usati per la misura e la caratterizzazione dei componenti elettrici, per la realizzazione di circuiti raddrizzatori di corrente, per il pilotaggio di determinati carichi e per la realizzazione di circuiti oscillatori.
CIRCUITI PER LA MISURAZIONE DI COMPONENTI
Si tratta di circuiti realizzati ed usati in generale per il condizionamento di sensori o quando si ha la necessità di effettuare misure molto precise su dei componenti. In questa sezione, vedremo i circuiti “classici” ed accenneremo all’amplificatore per strumentazione che spesso è possibile trovare proprio a valle di un circuito di misurazione.
IL PONTE DI WHEATSTONE
Il ponte di Wheastone prende nome da Charles Wheatstone che perfezionò il circuito precedentemente creato da Samuel Hunter Christie, per la misura delle resistenze elettriche. Nella Figura 1 viene mostrato un esempio di ponte di Wheatstone con quattro resistenze di uguale valore, i due rami del ponte, essendo connessi in parallelo, hanno la stessa tensione, sulle quattro resistenze scorre quindi la stessa corrente.
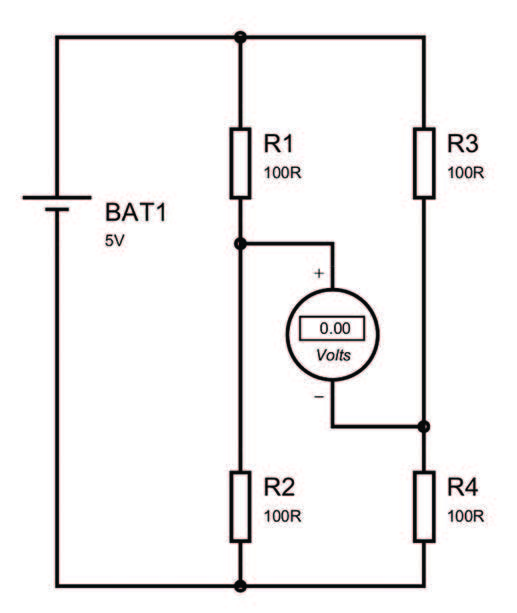
Figura 1: Ponte Bilanciato
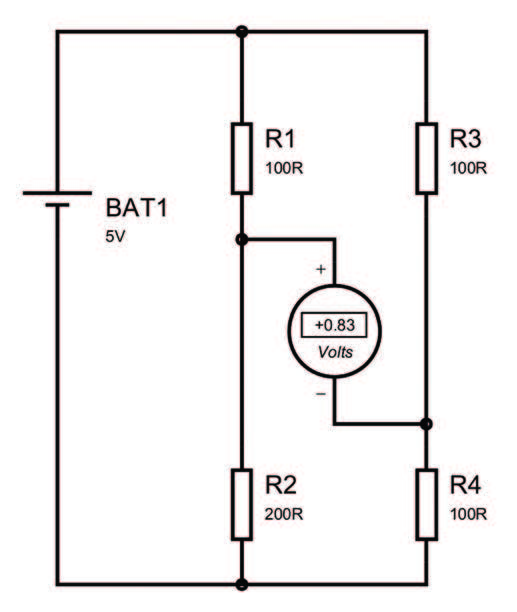
Figura 2: Ponte Sbilanciato
La tensione tra i centri dei due rami è data dalla differenza tra la tensione su R2 e la tensione su R4, essendo queste di uguale valore e scorrendo su queste la stessa corrente, le due tensioni sono uguali e quindi, come visibile in figura, la tensione tra i centri dei due rami è nulla. Nella Figura 2 invece viene mostrato uno schema circuitale con R2 diversa dalle altre, le tensioni su R2 e su R4 vengono date dai partitori:
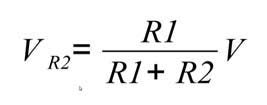

Pertanto, la tensione tra i centri dei due rami, facendo i calcoli equivale al valore riportato sulla figura (0.83V). Da questi due semplici calcoli si capisce il funzionamento e gli utilizzi del ponte di Wheatstone. Riscrivendo le formule si può ricavare il valore numerico di una qualsiasi resistenza conoscendo i valori delle altre tre presenti nel ponte nonché la tensione tra i centri dei due rami, se ad esempio si volesse ricavare il valore di R2, considerando le altre di uguale valore, R, e chiamando Vl la tensione letta tra i centri dei due rami si ottiene:
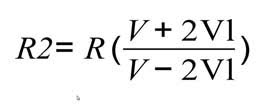
Che, considerando le configurazioni circuitali mostrate nelle Figure 1 e 2 restituisce l’esatto valore di R2, mostrato proprio nelle figure. Questo circuito è ampiamente utilizzato nei circuiti di condizionamento dei sensori resistivi, come ad esempio un circuito basato su una termoresistenza (PT100), ovvero una resistenza che cambia il proprio valore al variare delle temperatura.
IL PONTE DI MAXWELL
Questo circuito è una variante del ponte di Wheatstone e viene usato per la misura degli induttori, nella Figura 3 viene mostrato lo schema circuitale. In questa sede trascureremo i calcoli, soffermandoci soltanto sul principio di funzionamento. Il ponte viene alimentato da una tensione alternata mentre l’induttore viene modellato come la serie di un componente puramente induttivo (L1), ed uno puramente resistivo (R1).
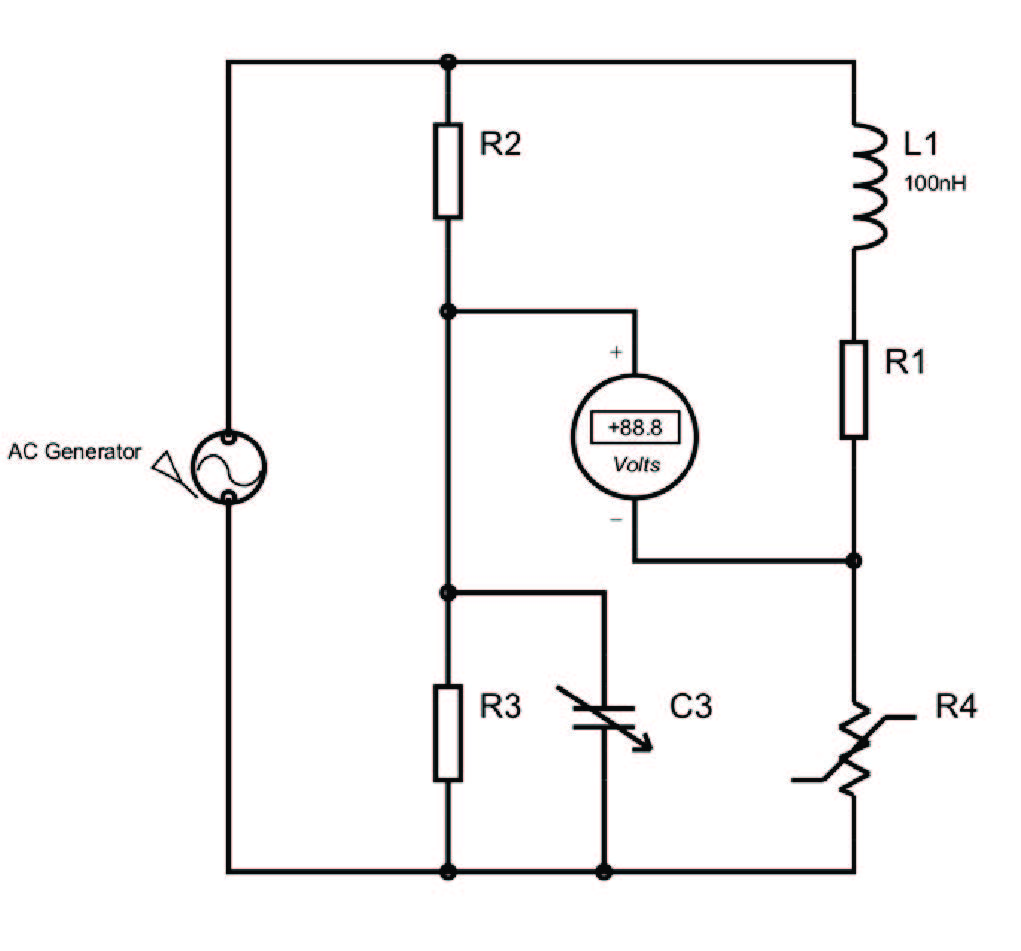
Figura 3: Ponte di Maxwell completo
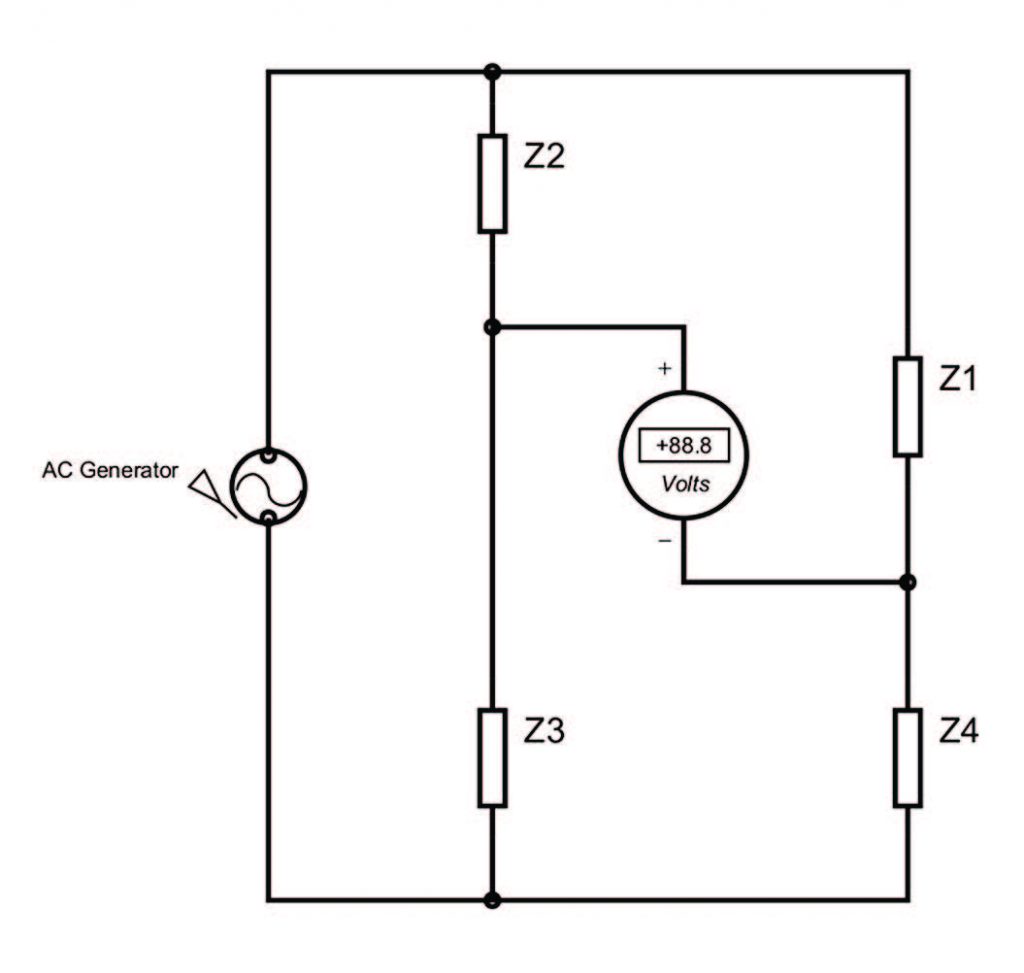
Figura 4: Ponte di Maxwell semplificato
Il calcolo di questi ultimi viene effettuato variando i valori della resistenza variabile (R4) e del capacitore variabile (C3) in modo tale da ottenere una tensione nulla tra i centri dei due bracci, mentre la resistenza che completa il ponte (R2) si suppone di valore noto. Considerando una tensione nulla tra i centri dei due rami del ponte, si ottiene facilmente la seguente relazione:
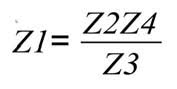
Scrivendo in dettaglio le espressioni delle varie impedenze presenti nella precedente espressione:

Si ottiene:
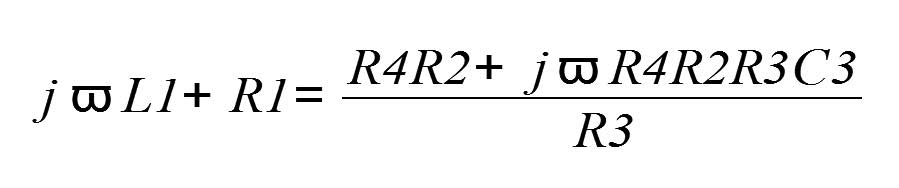
Infine, eguagliando le parti resistive e le parti reattive presenti in quest’ultima espressione si ottengono i valori di L1 ed R1, riuscendo così a stimare il valore dell’induttore presente nel ponte:
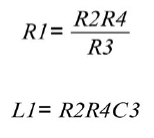
IL PONTE DI DE-SAUTY
Si tratta di un circuito per la misura delle impedenze, equivalente al ponte di Maxwell, quest’ultimo però si occupa del calcolo delle capacità. Il capacitore ignoto viene modellato come un condensatore in serie ad una resistenza e il valore di questi si ottiene modificando i valori dei condensatori e delle resistenze variabili presenti nel ponte fino a quando si annulla la tensione presente tra i centri dei due rami. In Figura 5 viene mostrato lo schema circuitale.
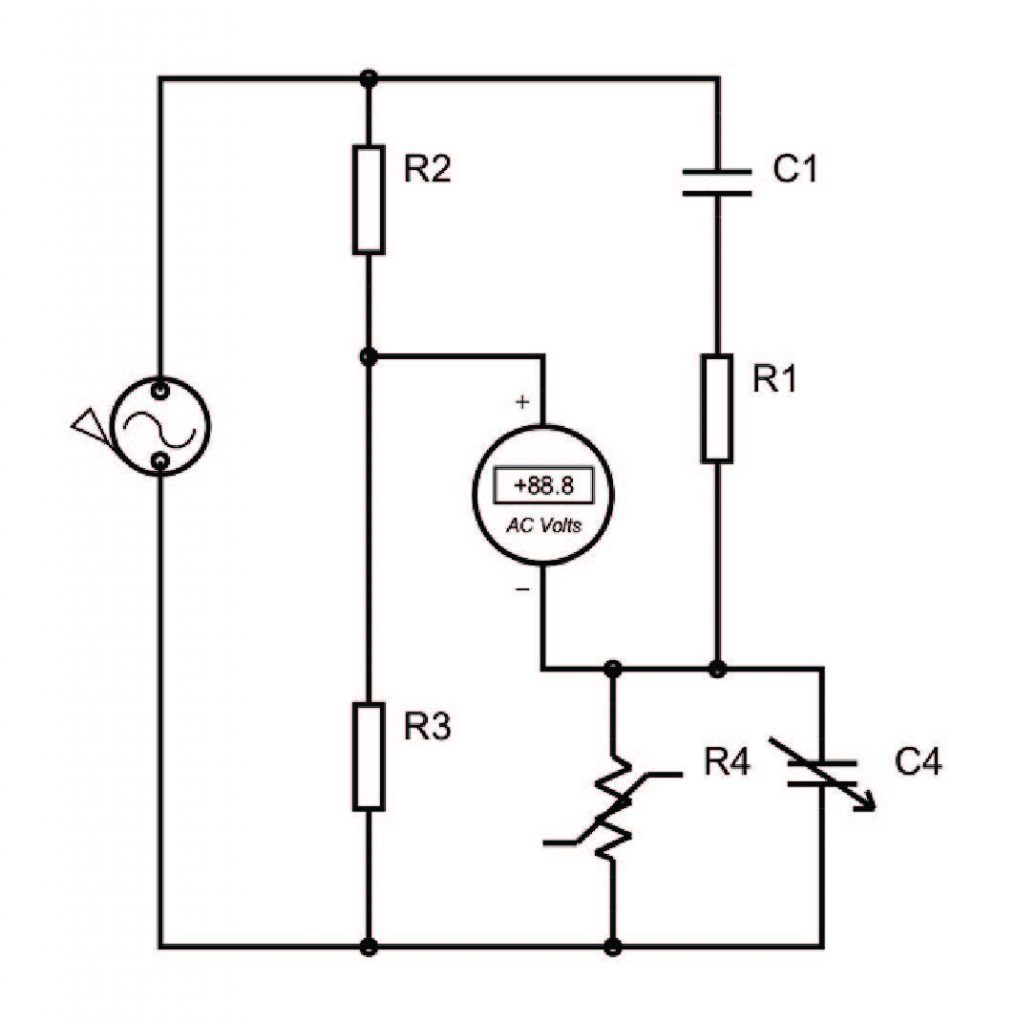
Figura 5: Ponte di De-Sauty
Considerando una tensione nulla tra i centri dei due rami del ponte, si ottiene facilmente la seguente relazione:
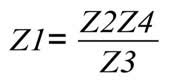
Scrivendo in dettaglio i valori delle varie impedenze presenti nella precedente espressione:
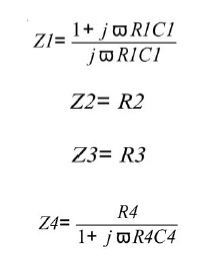
Si ottiene:
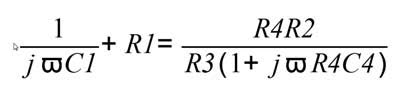
Infine, eguagliando le parti resistive e le parti reattive si ottengono i valori di C1 ed R1, riuscendo così a stimare il valore del capacitore presente nel ponte:






