L’elettronica, come la maggior parte dei rami scientifico ingegneristici, per l’interpretazione dei dati richiede la risoluzione di equazioni talvolta molto complesse. Ma come è possibile che un microprocessore sia in grado di eseguire un calcolo trigonometrico utilizzando solamente addizioni e sottrazioni?
I rami della matematica, e i teoremi ad essa legati, sono innumerevoli, spesso di difficile interpretazione e raramente implementabili, ma altre volte utili alla risoluzione di problematiche altresì incalcolabili. Da numerose ricerche effettuate, i consigli ricevuti per il calcolo del seno di un ipotetico angolo “x” utilizzando un PIC, riguardavano la realizzazione di una tabella: ogni parametro di x viene corrisposto in un determinato valore del seno. Certo, questo metodo risulta efficace nell’approssimazione, ma richiede l’utilizzo di un elevata quantità di memoria, e quindi poco performante in dispositivi con risorse contenute.
Serie di Taylor
La stima di una funzione utilizzando termini più semplici, quali i polinomi, e quindi la possibilità di analizzarne l’andamento in maniera più agevole, è fondamentale in molte questioni di analisi matematica. Ampie letture son dedicate all’indagine in questione, è proprio per questo che il paragrafo seguente non intende fornire nozioni algebriche, ma soltanto porre l’accento a riguardo di un modello alternativo per la descrizione e la risoluzione di calcoli complessi.
Il teorema di Taylor-Maclaurin
Gli sviluppi di Taylor prendono nome dall’omonimo matematico inglese Brook Taylor, che nel 1715 affermo:
”Qualsiasi funzione matematica può essere espressa sotto forma di somma di polinomi”. Sta di fatto però che, anche se il calcolo darà come risultato un numero sufficientemente preciso, ciò causerà in ogni modo un approssimazione standard: bassa più elevato sarà il grado del polinomio generato. Considerata una funzione f(x) numerica e reale, avente dominio appartenente all’intervallo chiuso [a,b], e sia xo un punto interno al dominio, si definisce polinomio di Taylor della funzione f(x):
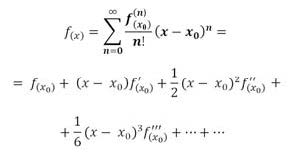
Nel nostro caso specifico, in cui il punto di partenza della funzione è sempre 0, si impone xo= 0, arrivando quindi alla forma generalizzata, detta anche di Mclaurin:
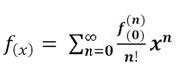
L’errore nelle approssimazioni
Il numero di termini della serie, per definizione, è infinito. Per ragioni di calcolo, si ha quindi la necessità di troncare l’espressione ad un determinato grado, causando un errore nella soluzione finale. Ovviamente, questa deviazione è direttamente legata al grado del polinomio, ed è calcolabile come:
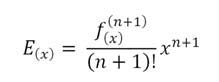
L’aggiunta di tale termine, risulta di difficile utilizzo, in quanto richiederebbe un tempo di svolgimento elevato, seppure fornendo il valore mancante per l’arrotondamento dell’espressione. Ivi per cui presi in considerazioni gradi considerevoli, superiori all’undicesimo, si reputa questo errore irrisorio dando modo di ignorarne il calcolo. Per ragioni di coerenza e di semplificazione, non si può evitarne la scrittura:
indicheremo quindi con o(xn) l’effettivo arrotondamento.
Generalizzazione con funzioni complesse
Vista la teoria presentata, si è giunti al momento di calcolare lo sviluppo di una delle funzioni trigonometriche fondamentali, dando in questo modo le basi per un’eventuale implementazione. Considerato sin(x), affermeremo secondo il teorema di Mclaurin:
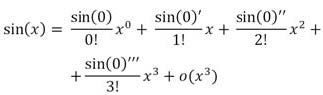
Eseguendo le derivate, si arriverà alla forma:
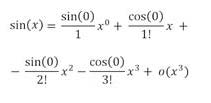
Da cui, sostituendo i valori noti del seno e del coseno:
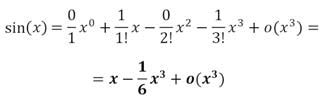
Risulta di facile interpretazione quindi, il vantaggio che gli sviluppi in serie di Taylor-Maclaurin forniscono nella risoluzione di espressioni complicate. I calcoli presentati qui sopra risultano utili solo a rendere chiaro l’utilizzo del teorema, in caso fossero necessari gli sviluppi di qualsiasi termine, una ricerca approfondita in internet, o in un libro di analisi matematica, forniranno l’intero gruppo di polinomi relativo.
Implementazione elettronica
Scendiamo ora nel dettaglio riguardante l’implementazione circuitale, che non riguarda solamente dispositivi programmabili, ma da libero spazio anche alla realizzazione di interfacce digitali. Ovviamente, la versatilità fornita da un breve codice, qualche volta non è neanche paragonabile anche allo schema più semplice e veloce, perché permette leggere modifiche senza uno sconvolgimento generale.
Il codice
Ripresa in esame la funzione trigonometrica sin(x) con l’intento di realizzare un algoritmo di calcolo per un PIC 16F84A, si nota dal codice seguente come l’implementazione diventa molto snella e rapida. Per comodità, e facilità di lettura, si son divisi i vari termini sotto forma di sei equazioni, permettendo al lettore un ampio spettro a riguardo del teorema di Mclaurin (listato 1).
void seno(float a) {
float primo, terzo, quinto, settimo, nono, undicesimo;
a = a*0.017453292519943; /*conversione del valore da gradi a radianti*/
primo = a; /*termine di primo grado = a */
terzo = (a*a*a)/6; /*termine di terzo grado = (a^3)/3! */
quinto = (a*a*a*a*a)/120; /*termine di quindi grado = (a^5)/5! */
settimo = (a*a*a*a*a*a*a)/5040; /*termine di settimo grado = (a^7)/7! */
nono= (a*a*a*a*a*a*a*a*a)/362880; /*termine di nono grado = (a^9)/9! */
undicesimo = (a*a*a*a*a*a*a*a*a*a*a)/39916800;
/*termine di undicesimo grado = (a^11)/11! */
seno = primo - terzo + quinto - settimo + nono - undicesimo;
}
| Listato 1 |
Due dei parametri che fanno di un algoritmo un “buon algoritmo”, sono: la velocità di esecuzione e la memoria utilizzata. Da numerose prove effettuate, la velocità d’esecuzione dell’algoritmo, con un quarzo a 4Mhz, è compresa tra i 70us e i 100us. Certo, più elevata di un qualsiasi altro algoritmo di ricerca, ma al contempo performante per applicazioni che richiedono tempi di risposta e valutazione immediati. La memoria non è sfruttata al massimo: la dichiarazione delle variabili all’interno della subroutine, da al codice la peculiarità di utilizzare 12 locazioni all’inter no della procedura. Ciò permette all’integrato, in caso di necessità future, di sfruttare la porzione di RAM occupata.
Conclusioni
Le serie di Taylor-Maclaurin possono essere personalizzate per adattarsi a vari tipi di calcolo. La possibilità di accettare parametri, e di sviluppare un espressione di conseguenza, realizzano una potenza di simulazione elevatissima. Resta comunque a libera discrezione del progettista l’effettivo utilizzo del teorema, analizzando approfonditamente le restrizioni che anch’esso impone.





Questo e’ solo un esempio di come implementare la matematica con l’elettronica. Anche la crittografia per esempio e’ una tipica applicazione.